Основные аспекты методики подготовки школьников к ЕГЭ

по математике в средней школе»

Содержание:

Введение………………………………………………………………………...….3

Глава 1. «Психолого-педагогические проблемы при подготовке к ЕГЭ»

1.1 Причины волнения и трудности при сдаче ЕГ по математике…...……..…5

1.2 Психологическое сопровождение ЕГЭ……………………….……….….….6

Глава 2. «Методические особенности при подготовке к ЕГЭ по математике»

2.1Особенности процесса подготовки ЕГЭ………………..………………..……8

2.2Формы подготовки к ЕГЭ и их характеристика ….…….……………..…..….9

2.3Этапы разработки программы подготовки к ЕГЭ по математике………….10

Глава 3. «Методика работы с задачным материалом при подготовке школьников к ЕГЭ по математике»

3.1 Организация повторения курса математики………………..…..…...………12

3.2 Группы задач для подготовки к ЕГЭ ……...………….…………………..…15

· Задачи типа №7……………………………………………..……………..…15

· Задачи типа №11……………………………………………………….....….16

· Задачи типа №13………………………………………………….….……...17

Заключение…………………………………………………………….……….…17

Библиографический список…………………………………………....….…….18

Приложение №1. Задачи для устного счета к заданию №1 ……...…….…...…20

Приложение №2. Задачи для повторения при изучении стереометрии …...…21

Приложение №3. Задачи по теме «Геометрический смысл производной»..…24

Приложение №4 . Решение неравенств методом интервалов……….………....26

Приложение №5. Задания по теме «Модуль числа»…………………….…..….30

Приложение №6. Задания типа №7…………………………………………..….32

Приложение №7. Группа задач типа №11……………………………………....36

Приложение №8. Группа задач типа №12…………………………………...….39

Приложение №9. Задачи на отработку способов отбора корней…………..….41

Приложение №10. Задачи типа №13…………….……………………………....45

Приложение №11. Факультативный курс по математике «Решение

уравнений с модулем»………………………………………………………..….47

Введение.

Единый Государственный Экзамен по математике направлен на контроль сформированности у выпускников математических компетенций, предусмотренных требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике. Варианты КИМ составлялись на основе кодификаторов элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения в ЕГЭ по математике.

ЕГЭ по математике является, с одной стороны, одним из двух обязательных экзаменов, который сдают все выпускники общеобразовательных учреждений, а с другой стороны, – одним из экзаменов, востребованных для поступления в вуз. Это определяет необходимость точной уровневой дифференциации заданий КИМ с учетом различных целевых установок участников экзамена и требований вузов к математической подготовке абитуриентов.

Руководитель федеральной группы разработчиков ЕГЭ по математике И.В.Ященко заявил, что результаты ЕГЭ по профильной и базовой математике в этом году гораздо лучше прошлогодних.

Результаты ЕГЭ по математике профильного уровня
	2016 год	2015 год
Набрали 60-80 баллов	127598	117580
Набрали 80-100	17668	5855
Набрали менее 27 баллов	74000	100000
Результаты ЕГЭ по базовой математике
Получили отличный результат	39,4%	31,2%
Не преодолели минимальный порог	4,7%	7,4%

Несмотря на улучшение показателей ЕГЭ, результаты экзамена выявили ряд нерешенных проблем, характерных для подготовки различных категорий выпускников:

· ориентация на прочное усвоение базовых требований к математической подготовке;

· дифференциация обучения, разработка стратегии обучения и подготовки к выпускному экзамену с учетом уже имеющегося у выпускника уровня образовательной подготовки.

Низкие результаты на ЕГЭ по математике волнуют и учеников, и родителей, и школьных учителей, и конечно же преподавателей вузов. Верным кажутся наблюдения и выводы учителей:

· К сожалению, школьники разучились системно мыслить, связно формулировать мысль, излагать текст, не владеют терминологией. Многие нынешние выпускники школ не стремятся к тому, чтобы получить прочные знания по математике.

· Недостаточное уделение времени преподаванию геометрии, практически исчезновение из школы черчения привело к тому, что у школьников не вырабатывается пространственное мышление. Это влечёт за собой разрушение системного мышления: зная отдельные факты, учащиеся не могут создавать из них логические построения.

Школьные учителя видят несколько причин в скромных результатах экзаменов по математике. Ряд педагогов по-прежнему считает, что наличие ЕГЭ как единственной формы итоговой аттестации заставляет «натаскивать» школьников на выполнение КИМов прошлых лет. Ещё одна группа опрошенных мной учителей говорит о том, что в нашем обществе у детей исчезла обязанность учиться, а у родителей – нести ответственность за воспитание своих детей. Школа для семей таких учеников превращается в своего рода «камеру хранения»: родители отправили ребенка в школу и на этом успокоились... Если школьник не хочет учиться, то никакое мастерство учителя не поможет. Увы, многие и дети, и взрослые забыли, что учёба – это труд.

За время моей работы по подготовке обучающихся к ЕГЭ я пришла к выводу о том, что результаты обучающихся на экзамене постоянно меняются. Исходя из этого я поставила перед собой цель: выявить проблемы выпускников при подготовке к ЕГЭ и найти пути их решения.

Для достижения поставленной цели необходимо решить следующие задачи:

ü Выявить психолого-педагогические проблемы подготовки выпускников к ЕГЭ по математике.

ü Рассмотреть методические особенности подготовки к ЕГЭ по математике.

ü Изложить методику подготовки школьников к ЕГЭ по математике.

ü Подобрать задачный материал, соответствующий вышесказанным методическим особенностям.

Глава1. ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЕ ПРОБЛЕМЫ ПРИ ПОДГОТОВКЕ К ЕГЭ.

1.1. Причины волнения и трудности при сдаче ЕГЭ по математике.

Проблемы подготовки к ЕГЭ – это поле деятельности не только педагогов, но и психологов. В настоящее время проблема методического сопровождения предметной подготовки к ЕГЭ в целом достаточно освещена.

Подготовка к единому государственному экзамену является одной из основных проблем выпускников. По своей сути ЕГЭ является своеобразной проверкой знаний, социальной и психологической готовности школьников к постоянно меняющимся условиям современной реальности. В этой связи, психологическая устойчивость старшеклассников является одной из основных характеристик, способствующих успешной аттестации в форме ЕГЭ.

Подготовка к ЕГЭ, как правило, должна проходить на протяжении 4-5 последних лет обучения. Учителя стараются подготовить школьников с помощью дополнительных занятий. Кроме того, старшеклассники посещают курсы, знакомятся с различными пособиями для подготовки к ЕГЭ, некоторые занимаются с репетиторами. Но степень тревожности, напряжения у выпускников не снижается. В свою очередь, повышенный уровень тревоги учащихся на экзамене приводит к дезорганизации деятельности, снижению концентрации внимания, работоспособности. Совершенно очевидно, что перед психологами, педагогами и родителями встает проблема охраны психического здоровья школьников, для решения которой необходима продуманная система мероприятий, предусматривающая создание стабильной благоприятной атмосферы, уменьшение вероятности возникновения стрессовых ситуаций и повышение функциональных возможностей школьников.

По результатам тестирования наших выпускников, наиболее значимыми причинами волнения выпускников являются:

ü сомнение в полноте и прочности знаний;

ü сомнение в собственных способностях: умении анализировать, концентрировать и распределять внимание;

ü психофизические и личностные особенности: быстрая утомляемость, тревожность, неуверенность в себе;

ü стресс незнакомой ситуации;

ü стресс ответственности перед родителями и школой.

Таким образом, условно можно выделить три группы трудностей ЕГЭ для детей:

· познавательные – связанные с особенностями переработки информации в ходе ЕГЭ, недостаточным объемом знаний, неспособностью гибко оперировать системой учебных понятий предмета (эти трудности являются результатом всего периода обучения в школе!);

· личностные – обусловленные особенностями восприятия учеником ситуации экзамена, его субъективными реакциями и состояниями, отсутствием возможности получить поддержку взрослых;

· процессуальные – связанные с самой процедурой единого государственного экзамена и отсутствием четкой стратегии деятельности.

1.2. Психологическое сопровождение ЕГЭ.

Для целенаправленной подготовки к ЕГЭ необходимо создание благоприятных психологических, организационных и методических условий подготовки к ЕГЭ еще задолго до того, как ученик начнет целенаправленно готовиться к итоговой аттестации.

По опыту моей работы предметную подготовку к сдаче ЕГЭ по математике целесообразно осуществлять задолго до 11 класса для выработки соответствующей базы знаний, умений и практического опыта. Начиная с 5-6 класса я нацеливаю ребят на ЕГЭ. Темам уроков, которые входят в кодификатор ЕГЭ, я уделяю особое внимание. Одно и тоже задание стараюсь сформулировать по-разному, решить одну и ту же задачу несколькими способами. Это позволяет психологически настроить ребят на то, что в КИМах ЕГЭ можно встретить формулировку задания отличную от учебника. Заблаговременная работа также дает возможность перераспределить дополнительную нагрузку, не связанную с подготовкой к ЕГЭ.

Одним из существенных аспектов психолого-педагогического сопровождения выпускника, на мой взгляд, является ознакомление родителей со способами правильного общения с ним, оказания ему психологической поддержки, создания в семье благоприятного психологического климата.

Работа с родителями нацелена на повышение осведомленности родителей и формирование реалистичной картины экзамена, снижение родительской тревоги.

В начале учебного года, я посещаю первое родительское собрание. На этих собраниях:

· знакомлю родителей с планом работы по математике на предстоящий учебный год;

· разъясняю позицию Министерства РФ по проблеме ЕГЭ,

· характеризую структуру контрольно измерительных материалов (КИМов) по математике;

· рассказываю о формах заданий и поясняю подходы к оценке результатов выполнения заданий разной формы;

· анализируя содержание проверяемых на экзамене разделов и тем школьного курса математики, обращаю внимание родителей какими знаниями, умениями и навыками должен обладать каждый ученик;

· знакомлю родителей с формами подготовки к ЕГЭ.

Психологическая подготовка к экзаменам способствует повышению уровня информированности, психологической готовности учащихся, родителей, педагогов в режиме подготовки и проведения ЕГЭ, если это – большая, длительная работа не только психолога с детьми, но и всего педагогического коллектива и родителей.

Глава2. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ

ПРИ ПОДГОТОВКЕ К ЕГЭ ПО МАТЕМАТИКЕ.

Математика является не только очень важным учебным предметом общеобразовательной школы, но и весьма сложным, так как математическими способностями обладают не многие школьники, а обучать математической грамоте необходимо всех и единый экзамен по математике сдают все. Кроме того, значительная часть обучающихся 10-11 классов после окончания школы хотят поступить в ВУЗы, в которых предъявляются достаточно высокие требования к математической подготовке абитуриентов и студентов.

В соответствии с вышесказанным можно выделить главную цель, к которой должен стремиться учитель: наряду с формированием новых знаний, умений и навыков включать ранее сформированные знания в деятельность ученика с целью повторения и систематизации знаний для подготовки к единому государственному экзамену.

Исходя из ведущей цели я определила следующие, важные, на мой взгляд, задачи:

ü систематизировать знания и умения за курс средней школы;

ü вооружить учащихся определенным кругом знаний, необходимых для поступления и обучения в ВУЗах;

ü систематизировать приемы решения различных уравнений и неравенств, систем уравнений;

ü научить выделять главное при решении задач, учить мыслить.

ü развивать творческие возможности ученика, привить умение самостоятельно пополнять знания;

ü развивать следующие качества: целеустремленность, самостоятельность, аккуратность, честность, трудолюбие, умение доводить начатое дело до конца, развивать и поддерживать устойчивый интерес к математике.

2.1 Особенности процесса подготовки ЕГЭ.

Подготовка к ЕГЭ - ответственное мероприятие, к которому нужно отнестись со всей серьезностью, ведь на карту поставлено многое. В случае неудовлетворительных результатов ЕГЭ сразу по двум обязательным предметам (русский язык, математика) учащийся не допускается к пересдаче в резервные дни и может получить лишь справку об обучении в школе.

Следует отметить, что в решении проблем с подготовкой к экзаменам не стоит уповать на школьного учителя, поскольку он вынужден одновременно заниматься с целым классом. Учебный материал имеет свои особенности, ученики усваивают его с разными скоростями и, не поняв чего-то сразу, часто не выясняют этого позже. В результате образуются «пробелы» в знаниях, не формируются необходимые умения и навыки по применению знаний и сдача будущих экзаменов может оказаться под угрозой.

На мой взгляд, залогом успеха на экзамене является именно комплексный подход к подготовке, в котором в качестве составляющих можно выделить три важных момента:

1) Организационный.

Как правило, подготовка к ЕГЭ занимает у учащихся достаточно много времени и требует, кроме умственных усилий еще и решение организационных вопросов (подача заявлений на сдачу экзаменов по выбору, подбор литературы для подготовки к ЕГЭ, поиск репетиторов и т.д.) Для этого целесообразно составить план подготовки, в котором нужно отразить ее основные этапы и сроки их реализации.

2) Образовательный.

Безусловно, самое главное в процессе подготовки к экзаменам - получить необходимые знания, умения и навыки по предмету. Школьная учебная литература достаточно полно раскрывает тематику предмета, но также нужно использовать и дополнительную литературу, отражающую специфику предстоящего экзамена. К ней относятся контрольно-измерительные материалы (КИМ-ы), методические разработки, учебные пособия, электронные учебные курсы, множество сайтов для подготовки к ЕГЭ, курсы довузовской подготовки и многое другое.

3) Психологический.

ЕГЭ отличается непривычным для учащихся форматом проведения. Продолжительность экзамена - четыре часа, все бланки экзаменационных документов должны заполняться специальным образом, существуют определенные правила поведения на экзамене, при невыполнении которых организаторы могут удалить участника с экзамена. Всё это, в совокупности с большим значением результатов экзамена для выпускника, может обусловливать излишнее волнение на экзамене и, как следствие, потерю сосредоточенности, ослабление уверенности в своих силах из-за страха совершить ошибку. Поэтому при подготовке к ЕГЭ очень важно уделять внимание изучению процедуры проведения экзамена, правил заполнения бланков и периодически практиковаться на экзаменационных материалах прошлых лет в условиях, приближенных к реальному экзамену.

2.2. Формы подготовки к ЕГЭ и их характеристика.

Своим ученикам я предлагаю следующие формы подготовки к экзаменам:

1) Самоподготовка.

Учащийся самостоятельно принимает все решения относительно количества занятий, их частоты и объема изучаемого материала. Данный способ имеет самый высокий риск недостижения экзаменационной цели. Действительно, большинство учащихся 11-х классов сами не смогут правильно выстроить систему подготовки к экзаменам. Кроме этого, процесс самостоятельного устранения «пробелов» в знаниях или усвоения нового материала стоит больших моральных и умственных усилий. Электронные обучающие системы и видеокурсы подготовки к ЕГЭ, методические пособия, онлайн-тесты, тематические группы в социальных сетях частично облегчают труд учащегося при самоподготовке.

2) Занятия на подготовительных курсах.

Такие курсы могут организовываться ВУЗами, школами и негосударственными образовательными учреждениями.

В учебном плане 10-11 классов нашей школы имеется 1 дополнительный час в неделю учебных элективных занятий в рамках подготовки к ЕГЭ по математике. Кроме того, создан график дополнительных консультативных занятий по математике. Причем, дети подразделяются на группы по уровню знаний (базовый и профильный). Посещаемость учащимися этих занятий контролирует классный руководитель и преподаватель. Выясняются причины отсутствия ученика на занятии, сведения доводятся до родителей. Таким образом происходит сотрудничество классного руководителя – учителя-предметника – родителя.

Некоторые наши ученики посещают курсы организованные ВУЗами, в который они планируют поступить. В нашем городе один раз в месяц работает «Школа абитуриента». Занятия в этой школе проводят учителя-математики из разных школ города. Мои ученики, по мере возможности, посещают данные занятия.

Серьезным недостатком занятий на подготовительных курсах является невозможность для ученика получить от преподавателя индивидуальный подход, чтобы ликвидировать собственные «пробелы» в знаниях. Кроме этого, если говорить о вузовских курсах, то преподаватели высшей школы зачастую переносят специфику преподавания в ВУЗах на учащихся школ. Это усложняет процесс усвоения учащимися необходимой информации, что в совокупности с недостаточным контролем в процессе обучения может приводить к невысоким результатам ЕГЭ.

3) Занятия с репетитором.

Подготовка к единому государственному экзамену требует индивидуального, личностно-ориентированного подхода. Для реализации такого подхода идеально подходят занятия с репетитором, которые могут проводиться в двух режимах: индивидуальные занятия и в мини-группах. К сожалению, очень мало моих учеников могут позволить данные занятия, так как материальный уровень большинства семей наших выпускников ниже среднего и низкий.

2.3 Этапы разработки программы подготовки к ЕГЭ по математике.

В начале учебного года мы с ребятами разрабатываем программу подготовки к ЕГЭ по математике. Каждый ученик определяет свои возможности и способности для себя, так как они у всех ребят разные. Охарактеризую основные этапы разработки программы подготовки к ЕГЭ с учетом особенностей аспектов: организационного, образовательного и психологического.

1этап. Определить цели подготовки.

При составлении программы я объясняю ребятам, чтобы они не ставили перед собой цель, например, «научиться решать такие-то задачи» или «выучить такие-то темы», а сформулировали их в виде желаемого результата экзамена. Например, сдать ЕГЭ «не меньше чем на 70 баллов», «хотя бы на 60 баллов» и пр. Данный подход позволяет сразу сориентироваться на круг рассматриваемых вопросов по математике и представить себе за счет каких типов заданий будут набираться желаемые баллы.

2этап. Собрать максимум информации о предстоящем экзамене.

В кабинете математики оформляется тематический стенд «Готовимся к ЕГЭ», на котором имеется вся необходимая информация о структуре, порядке и сроках проведения, важные особенности и методика оценивания ЕГЭ по математике. Ежегодно в каждом выпускном классе проходят классные собрания, на которых рассматриваются вопросы сдачи ЕГЭ. На дополнительных занятиях мы с ребятами разбираем кодификатор ЕГЭ с целью выявления пробелов в знаниях. По результатам изучения собранной информации учащийся должен ясно представлять себе как проходит экзамен, какие виды заданий используются, каковы критерии оценивания результатов экзамена. Сюда же относится и подбор методической литературы - это могут быть разнообразные учебные пособия, подборки контрольно-измерительных материалов экзаменов прошлых лет и пр. Много подобной литературы для ознакомительных целей представлена в Интернете и доступна для свободного скачивания. Большой подбор методической литературы имеется в кабинете математики школы.

3этап. Приступить к выбору формы подготовки.

После того как ученики определились с целью и подробно узнали о предстоящем экзамене, я, как учитель, предлагаю своим ученикам формы подготовки к ЕГЭ по математике: самоподготовка, занятия на подготовительных курсах и занятия с репетитором.

Наиболее распространенной формой у наших ребят являются занятия на подготовительных курсах, организованных в нашей школе. Так как занятия с репетитором и на курсах довузовской подготовки требуют финансовых затрат, наши выпускники пользуются этой услугой крайне редко.

4 этап. Определить сколько времени имеет учащийся на подготовку к экзаменам.

Вся первая половина дня у учеников проходит в школе, а после нее многие посещают еще и различные спортивные секции, музыкальные школы и прочие подобные заведения. Кроме того, нужно еще выполнять домашнее задание и уделять время полноценному отдыху. Таким образом, при ближайшем рассмотрении получается, что времени на подготовку не так уж и много, как может показаться на первый взгляд. Тем не менее, слишком частые занятия тоже не приведут к цели, так как очень быстро может наступить эмоциональная и умственная «перегрузка» ученика. Для того, чтобы этого не произошло я своим ученикам задаю дифференцированные домашние задания, организую дополнительные задания для более сильных учеников.

5 этап. Контролировать ход процесса подготовки к экзаменам.

Здесь на первый план выходит не контроль за прохождением занятий, а контроль продвижения вперед, освоения предмета. В течение учебного года выпускного класса ребята очень много пишут различных диагностических работ МИОО «СтатГргад» и пробных ЕГЭ по математике, проводимых Департаментом образования ТМР. Я, как учитель математики, провожу мониторинг: веду карту выполнения работ на каждого ученика и класса в целом. Это позволяет увидеть системные ошибки, пробелы в знаниях конкретных учеников и скорректировать мою работу, как учителя-предметника.

Глава3. МЕТОДИКА РАБОТЫ С ЗАДАЧНЫМ МАТЕРИАЛОМ ПРИ ПОДГОТОВКЕ ШКОЛЬНИКОВ К ЕГЭ ПО МАТЕМАТИКЕ.

В структуре ЕГЭ содержится указание на то, как можно выстроить подготовку: существующий кодификатор позволяет разбить материал на несколько крупных тематических блоков. Повторение можно выстроить по содержательным: вычисления, буквенные выражения, уравнения, неравенства; и функциональным линиям: все функции и элементы математического анализа. Такой подход будет способствовать формированию более прочных знаний и, как следствие, более уверенному поведению выпускника на экзамене.

Неотъемлемым элементом подготовки к ЕГЭ является обучение заполнению бланков. Эту работу я, как учитель-предметник, веду с 10 класса.

3.1.Организация повторения курса математики.

Единый государственный экзамен по математике, привнесенный в российское образовательное пространство, имеет свои сильные и слабые стороны. Чтобы минусы обратить в плюсы, учителю, который готовит школьников к экзамену, в первую очередь необходимо знание о формате и структуре ЕГЭ, особенностях процедуры его проведения. Эта информация важна в первую очередь для учителя, который учит школьников и готовит их к экзамену. ЕГЭ помогает решать такую важную задачу, стоящую перед учителем, как освоение технологий обучения и организации итогового повторения, позволяющих выпускникам демонстрировать уровень своих знаний не ниже своей годовой отметки.

Возможностей для организации эффективного обобщающего повторения и продуктивной подготовки к экзаменам в настоящее время довольно много. Главное — не подменять итоговое повторение бессистемным решением (и уж тем более — бездумным заучиванием решений) того или иного числа задач. При грамотной организации итогового обобщающего повторения удастся диагностировать проблемные зоны в знаниях учащихся, закрыть их, овладеть общими навыками решения задач различных типов, эффективно и продуктивно подготовить учеников к экзамену и, в конечном счете, обеспечить их необходимым багажом для продолжения образования.

Подготовка к ЕГЭ по математике не сводится к «натаскиванию» выпускника на выполнение определенного типа задач, содержащихся в демонстрационной версии экзамена. Подготовка к экзамену означает изучение программного материала с включением заданий в формах, используемых при итоговой аттестации. Кроме того, необходимо выявить и ликвидировать отдельные пробелы в знаниях учащихся. Одновременно надо постоянно выявлять проблемы и повышать уровень каждого учащегося в следующих областях (хорошо известных каждому учителю): арифметические действия и культура вычислений, алгебраические преобразования и действия с основными функциями, работа с неравенствами и уравнениями, понимание условия задачи, решение практических задач, самопроверка.

Задания типа №1 проверяют умение выполнять арифметические действия, делать прикидку и оценку. Эти задания являются, действительно, очень простыми, что вводит учеников в заблуждение, и они начинают искать подвох. Единственной сложностью этих заданий является то, что, получив в результате решения дробный ответ, в бланк записывается целое число.

При решении этого задания следует вспомнить, что такое процент. Для устной работы на уроке можно использовать простые задания на нахождение процента и прикидку. (Приложение №1)

При изучении стереометрии необходимо, прежде всего, уделять внимание формированию базовых знаний курса стереометрии (угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями, многогранники и т.д.). Для этого необходимо использовать задачи по готовым чертежам. Их можно включить в устный счет, повторение пройденного материала или закрепление нового материала. (Приложение №2)

Одновременно необходимо находить возможность восстанавливать базовые знания курса планиметрии (прямоугольный треугольник, решение треугольников, четырехугольники и т.д.). При изучении геометрии необходимо повышать наглядность преподавания, больше уделять внимания вопросам изображения геометрических фигур, формированию конструктивных умений и навыков, применению геометрических знаний к решению практических задач.

При изучении начал анализа следует уделять большее внимание пониманию основных идей и базовых понятий анализа:

· определять значение функции по значению аргумента при различных
способах задания функции; описывать по графику поведение и
свойства функций, находить по графику функции наибольшие и
наименьшие значения; строить графики изученных функций

· вычислять производные и первообразные элементарных функций,
исследовать в простейших случаях функции на монотонность,
находить наибольшие и наименьшие значения функций.

Так как выпускники допускают много ошибок при выполнении заданий по данной теме. Для отработки этих задач нужно применить задания с разными формулировками. (Приложение №3)

За два года старшей школы к изученным ранее функциям добавляются тригонометрические функции, показательная функция и логарифмическая функция. Именно с этими функциями, как правило, связано большинство задач ЕГЭ. Успешная сдача экзамена невозможна без знания свойств этих функций и уверенного владения ими применительно к задачам различных типов. Поэтому организовать обобщающее повторение в 11-м классе можно и по функциональным линиям: «Многочлены», «Рациональные функции», «Иррациональные функции», «Тригонометрические функции», «Показательная функция», «Логарифмическая функция». В этом случае внутри каждого функционального блока следует выделить однотипные содержательные блоки: числовые и буквенные выражения, уравнения и системы уравнений, неравенства и системы неравенств, производная и первообразная, исследование функций.

При подготовке к ЕГЭ необходимо повторить метод интервалов, так как он используется при решении многих видов неравенств: тригонометрических, логарифмических, иррациональных, квадратных, показательных и т.д.

Метод интервалов, используемый в решении неравенств, позволяет сделать решение более осмысленным в их изучении. (Приложение №4)

Несмотря на то, что тема «Модуль числа» проходит «красной нитью» через весь курс школьной и высшей математики, для ее изучения по программе отводится очень мало времени (в 6 классе -2 часа, в 8 классе - 4 часа).

Исходя из всего вышесказанного, учителю необходимо находить разнообразные методические приемы, использовать различные подходы и методы в обучении решению задач с модулем. Как показывает практика, выпускники часто забывают, что такое модуль. Для этого необходимо на факультативных или дополнительных занятиях повторять и отрабатывать тему «Модуль». (Приложение №5)

Для организации подготовки школьников к экзамену учителю рекомендуется прежде всего выявлять целевые группы, например:

Для каждой целевой группы можно сформулировать несколько принципов организации подготовки к ЕГЭ.

Первая целевая группа – учащиеся, которые поставили перед собой цель – преодоление нижнего рубежа (базовый уровень) для получения аттестата.

Работа должна быть построена так, чтобы за месяц до итоговой аттестации закончить рассмотрение всех выбранных позиций заданий совмещая работу с регулярным тематическим повторением и отработкой базовых математических навыков.

Раз в месяц можно проводить зачетную работу (аудиторную или домашнюю, индивидуальную или групповую) по выбранным задачам. Общая цель такой работы – отработать решение выбранных заданий и вселить уверенность в учащихся, что нижний рубеж им по силам.

Вторая целевая группа – учащиеся, которые поставили перед собой цель – получить не очень высокие баллы (на уровне 50-60 баллов по 100-балльной шкале), но достаточные для поступления в вуз, не предъявляющий высоких требований к уровню математической подготовки;

Для этой группы необходимо уверенно выполнять 10-11 заданий профильного уровня.

Работа должна быть построена так, чтобы за два месяца до итоговой аттестации закончить рассмотрение всех позиций части 1 ЕГЭ профильного уровня, и к моменту итоговой аттестации закончить систематическое повторение тем, соответствующих выбранным позициям второй части .

Для учащихся этой целевой группы желательно регулярное проведение тренировочных работ, состоящих из заданий части 1 и выбранных позиций части 2, в частности, формируемых на базе работ, публикуемых на сайте Открытого банка математических задач.

Третья целевая группа – учащиеся, которые поставили перед собой цель – получить высокие баллы в профильном уровне (больше 60 баллов по 100 балльной шкале), необходимые для поступления в вуз, предъявляющий высокие требования к уровню математической подготовки абитуриентов.

Для этой группы необходимо отработать умение уверенно выполнять задания 1-15, уметь выполнять (может, с некоторыми недочетами) задания 16-17, стараться выполнить задания высокого уровня 18 и 19.

Чтобы научить решать выпускников задания №13, №14, №15, необходимо сначала привести типичные примеры вместе с их решением и комментариями и только после обсуждения дать варианты самостоятельных работ.

3.2. Группы задач для подготовки к ЕГЭ.

Мои наблюдения показывают, что у выпускников, сдававших профильный уровень, вызывают затруднение задания типа В8, В11, В12 и задания повышенного уровня №13. Конечно, у детей «группы риска», т.е. слабо подготовленных ребят затруднения вызывают и другие задания. В данной работе невозможно проработать все виды задач, поэтому я остановилась на вышеуказанных заданиях.

· Задачи типа №7

Задачи группы №7 связаны с вычислением производной. С исследованием графиков производной функции либо самой функции, определением экстремумов по заданному графику.

Типичные ошибки при выполнении заданий №7:

1. Обучающие часто путают графики функции и ее производной;

2. Допускается много ошибок в нахождении точек максимума и минимума. Многие считают, что если функция убывает, значит при пересечении о осью абсцисс - это точка минимума, на самом деле - это точка максимум, т.к. график идет с положительной области в отрицательную область.

3. Выпускники не внимательно следят за промежутками, на которых требуют что-то найти. Иногда этот промежуток никто не замечает, а значит решает задачу относительно всего зарисованного графика, а не заданной его части. (Приложение №7)

· Задачи типа №11

Текстовые задачи вызывают трудности у многих школьников. Чтобы решить задачу необходимо не только внимательно прочитать условие задачи, но и разобраться каким способ ее решать: по действиям, уравнением, системой уравнений, а может неравенством или системой неравенств. Необходимо разобраться, что требуется определить в задаче и записать правильный ответ.

Процесс решения текстовых задач включает три основных этапа:

· Составление математической модели.

· Работа с математической моделью.

· Ответ на вопрос задачи.

Самым сложным для учащихся является составление математической модели, то есть анализ текста задачи и поиск способа ее решения.

Все текстовые задачи можно разделить на:

· задачи на пропорции и проценты;

· задачи на работу;

· задачи на движение;

· задачи на концентрацию, смеси и сплава. (Приложение №7)

· Задачи типа №12

Задача очень похожа на №7, отличие заключается в том, что в №7 работали с графиками, а в №12 с функцией.

Типичные ошибки при выполнении заданий №12:

1. Обучающиеся забывают проверить на принадлежность заданному отрезку корней уравнения (точек экстремума);

2. Выпускники могут перепутать максимум и минимум.

3. Очень часто ребята не внимательно читают условие задачи. В результате вместо наибольшего (наименьшего) значения функции на заданном отрезке находят точку максимума (минимума). (Приложение №8)

· Задачи типа №13

Задание №13 повышенного уровня сложности на умение решать тригонометрические уравнения и отбирать корни, соответствующие определенному промежутку. Еще одной спецификой тригонометрических уравнений является неединственность формы записи ответа. Необходимо отработать упражнений с подобными заданиями. Для этого надо разобрать все возможные варианты отбора корней. (Приложение №9)

Учащиеся должны уметь выделять и решать следующие виды тригонометрических уравнений:

· квадратные, относительно одной из тригонометрических функций (или приводимые к ним);

· однородные уравнения первой и второй степени;

· комбинированные уравнения. (Приложение №10)

ЗАКЛЮЧЕНИЕ.

Экзамены воспитывают в сдающем чувство ответственности, что очень важно в педагогическом отношении. Если они и требуют большой затраты энергии и сил, причиняют воспитанникам много волнений и беспокойства, то и в этом можно видеть прекрасную подготовку к жизни, вовсе не усеянной розами. Однако такого взгляда на экзамены держатся далеко не все в педагогическом мире. Особенно не согласны с ним врачи и родители. Первые настаивают на том, что экзамены безусловно вредны для здоровья учащихся; установлено, например, что во время экзаменов ученики теряют в весе, чаще происходят нервные срывы у выпускников. Родители и некоторые педагоги полагают, что контролировать учителей и учеников надо в продолжение всего учебного года и так рационально поставить этот контроль, чтобы экзамены стали не нужны. Во время экзамена ученик находится в совершенно особенном, ненормальном состоянии, что вместе с краткостью времени не позволяет считать его ответ надежным показателем его знаний. Сам характер обучения, по мнению противников экзаменов, принимает весьма нежелательные формы, превращаясь у иных преподавателей в сплошное натаскивание к экзаменам.

Многие обучающиеся в году небрежно относятся к своим обязанностям, надеясь к экзаменам всё подогнать и восполнить все пробелы; уровень познаний, таким образом, понижается, а отнюдь не повышается, как утверждают защитники экзаменов. Решающее значение экзаменов заставляет учеников прибегать к разным уловкам и обманам (шпаргалки и прочее), лишь бы получить удовлетворительную отметку, и в этом смысле экзамены имеют деморализующее влияние на учеников.

Таким образом, еще раз подчеркну необходимость комплексного подхода при организации подготовки обучающихся ЕГЭ. При этом желательно не оставаться «один на один» с предметом, а воспользоваться помощью квалифицированного репетитора, который сможет выстроить процесс подготовки с учетом вышеназванных особенностей.

Итоги ЕГЭ предыдущих лет позволяют высказать некоторые общие рекомендации, направленные на совершенствование процесса преподавания и подготовки учащихся средней школы.

· Необходимо совершенствовать методику формирования базовых умений, составляющих основу математической подготовки выпускников средней школы.

· Анализ результатов выполнения базовых заданий по курсу алгебры и начал анализа показал наличие положительной динамики в овладении материалом раздела «Тригонометрия». В настоящее время вызывают тревогу низкие результаты выполнения заданий на решение иррациональных уравнений и логарифмических неравенств. Учителям в процессе обучения следует обратить внимание на обеспечение более прочного усвоения учащимися стандартных алгоритмов решения этих уравнений и неравенств.

· Геометрическая подготовка выпускников школы продолжает оставаться невысокой, поэтому по-прежнему необходимо усиленное внимание учителей к преподаванию курса геометрии в основной и старшей школе, чтобы в процессе обучения учащиеся не только овладевали теоретическими фактами курса, но и приобретали умения проводить обоснованные рассуждения при решении геометрических задач и математически грамотно записывать полученное решение.

Опыт моей работы показывает, что подготовку к ЕГЭ необходимо начинать с 5 класса. Для успешной сдачи ЕГЭ недостаточно 5 уроков в неделю. Необходимо работать над заданиями повышенной и высокой уровней сложности на дополнительных занятиях и факультативах.

Целенаправленной подготовке к ЕГЭ способствуют факультативные курсы. В приложении №11 представлен факультатив «Решение уравнений с модулем».

Поставленные в начале работы цели и задачи решены. Материалы, представленные в моей работе, могут быть использованы в дальнейшем при подготовке выпускников к ЕГЭ.

Библиографический список.

1. 1.http://schoolmathematics.ru/zadanie-s1-2

2. http://scool1-tulsky.edusite.ru/p50aa1.html

3. http://www.fipi.ru/binaries/1084/mat11.pdf

4. http://scepsis.ru/library/id_2480.html

5. http://ege-ok.ru/2012/03/28/ugol-mezhdu-pryamoy-i-ploskostyu-metod-koordinat-zadanie-s2/

6. http://festival.1september.ru/articles/591233/

7. http://knowledge.allbest.ru/mathematics/d-2c0a65635b2bc68b5d53b88421316c27.html

8. http://nsportal.ru/shkola/algebra/library/sistema-podgotovki-k-ege

9. Математика: «Решение тестовых задач»: экспресс-репетитор для подготовки к ЕГЭ / И.С.Слонимская, Л.И.Слонимский. – М.: АСТ: Астрель; Владимир: ВКТ, 2014.

10. Математика. Тесты к ЕГЭ / А.Г.Клово. – Ростов н/Д: Феникс, 2015.

11. http://nsportal.ru/shkola/materialy-metodicheskikh-obedinenii/library/sistema-raboty-uchitelya-matematiki-po-podgotovke

12. Алгебра и начала анализа: учеб. Для 10-11 кл. общеобразоват. Учреждений / [А.Н.Колмогоров, Ю.П.Дудницын и др.]; под ред. А.Н.Колмогорова. – 16-е изд. – М.: Просаещение, 2014. – 384с.

13. Математика №5, 2012; Т.Ермишигна «Обучение поиску решения».

14. http://www.cleverstudents.ru/maximum_minimum.html

15. Корикова Т.М., Суслова И.В. Элементарная математика. Стереометрия: учебное пособие. – Ярославль: Изд-во ЯГПУ, 2010.-114с.

16. Математика №5, 2011; А.Корянов, А.Прокофьев «Различные подходы к решению задач С5 ЕГЭ»

17. Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов/ сост. Г.И.Ковалева, Т.И.Бузулина, О.Л.Безрукова, Ю.А.Розка. – Волгоград: Учитель, 2008. -494 с.

18. ЕГЭ-2017. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов / под ред. И.В. Ященко. – М.:Издательство «Национальное образование», 2017. – 256 с. – (ЕГЭ, ФИПИ - школе)

19. http://edj77.narod2.ru/ege/matem/

20. http://festival.1september.ru/articles/507334/

ПРИЛОЖЕНИЯ.

Приложение №1

Задачи для устного счета к заданию №1

· Найдите 30% от 27. (8,1)

· Какое число получиться, если 140 увеличить на 60%? (224)

· Кафельная плитка продается коробками по 6 м². Сколько коробок плитки нужно купить, чтобы хватило на облицовку стен площадью 35 м^2.? (6)

· Билеты в ботанический сад стоит 50 рублей. Сколько рублей сдачи нужно получить с 2000 рублей, заплаченных за проход 36 человек? (200)

· Горные лыжи стоят 16 000 рублей. Сколько рублей будут стоить горные лыжи во время сезонной распродажи, когда на них объявлена скидка 20%? (12800)

· Йогурт стоит 7 рублей 60 копеек. Какое максимальное количество йогуртов можно купить на 50 рублей? (6)

· Шариковая ручка стоит 7 рублей. При покупке более 50 ручек на всю покупку начинает действовать скидка 20 %. Сколько рублей нужно заплатить при покупке 120 ручек? (672)

Приложение №2

Задачи для повторения или закрепления при изучении стереометрии.

Задание №1.

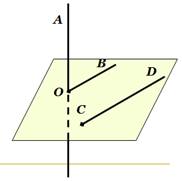
Дано: ОВ || СD, ОА и СD – скрещивающиеся. Найти угол между ОА и СD, если:

1) ˂АОВ=40º (40º)

2) ˂АОВ=135º (45º)

3) ˂АОВ=90º (90º)

Задание №2 .

Треугольники АВС и АСD лежат в разных плоскостях. РК – средняя линия ∆АDC с основанием АС. Определить взаимное расположение прямых РК и АВ, найти угол между ними, если ˂АСВ=80º, ˂В=40º

Ответ: 1) АВ и РК – скрещивающиеся прямые

2)60º

Задание №3.

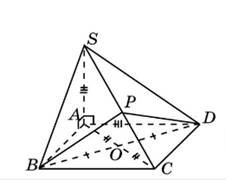Для пирамиды, изображенной на рисунке назовите номера верных утверждений:

1)Угол между плоскостями SAB и DBC прямой;

2)Плоскости SAB и SBС перпендикулярны;

3)Плоскости SАС и DBC перпендикулярны;

4)Угол между плоскостями SDC и DBC прямой;

5)Плоскости DBC и АSР перпендикулярны;

6)Угол между плоскостями SВC и АSР прямой Ответ: 1), 3), 5)

Систематизация знаний учащихся о нахождении расстояния между скрещивающимися прямыми может быть осуществлена с помощью следующей таблицы:

*Чертежи*	*Основные приемы вычисления расстояния между скрещивающимися прямыми*
	1. Построить общий перпендикуляр к а и в (его изображение на плоскости) и вычислить его длину. Используя векторный метод, достаточно предположить, что МN – общий перпендикуляр к а и в, выбрать векторный базис, разложить вектор М¯N по базисным векторам. Из условий М¯N ·А¯В=0 и М¯N·S¯С=0 найти коэффициенты разложения МN по базисным векторам, а затем и длину вектора М¯N.
	2. Через одну из скрещивающихся прямых провести плоскость, параллельную другой прямой. Найти расстояние от прямой до построенной плоскости (найти расстояние от любой точки второй прямой до ее ортогональной проекции на построенную плоскость)
	3. Через одну из скрещивающихся прямых провести параллельные между собой плоскости и найти расстояние между ними (найти длину перпендикуляра, проведенного из произвольной точки одной плоскости к другой плоскости)
	4. Провести плоскость, перпендикулярную одной из двух данных скрещивающихся прямых, а затем найти расстояние от точки пересечения этой прямой с плоскостью до проекции другой прямой на ту же плоскость.

	4₁. Если скрещивающиеся прямые взаимно перпендикулярны, то через одну из этих прямых провести плоскость, перпендикулярную второй прямой, а затем найти расстояние от точки пересечения ее с плоскостью до первой прямой.

	5. Если скрещивающиеся прямые принадлежат соответственно двум взаимно перпендикулярным плоскостям и одна из них перпендикулярна линии пересечения этих плоскостей, то провести через точку пересечения первой прямой с линией пересечения плоскостей перпендикуляр к другой прямой и найти длину соответствующего отрезка.

	6. Если на двух скрещивающихся прямых взяты точки А и В, С и D соответственно так, что объем пирамиды АВСD равен V, АВ=а, СD=в, ɣ=˂(АВ, СD), то p(AB, CD) =

Приложение №3

Задачи по теме «Геометрический смысл производной»

Задание №1.

(геометрический смысл производной)

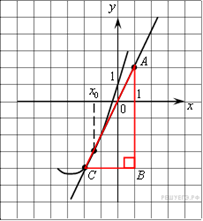
На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .

Ответ: 2

Задание №2 .

(определение промежутков знакопостоянства производной по графику функции)

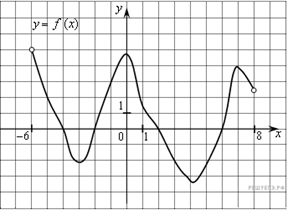
На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.

Ответ: 4

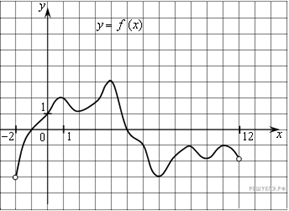
Задание №3 .

(нахождение точек экстремума функции по ее графику)

На рисунке изображен график функции , определенной на интервале (-2; 12). Найдите сумму координат точек экстремума функции .

Ответ:44

Задание №4 .

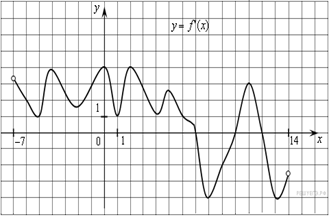(нахождение точек экстремума функции по графику производной функции)

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек максимума функции на отрезке .

Ответ: 1

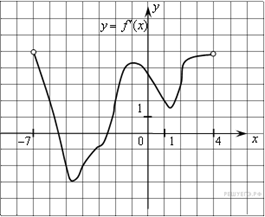Задание №5 .

(определение промежутков монотонности функции по графику производной функции)

На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму координат целых точек, входящих в эти промежутки.

Ответ: -3

Приложение №4

Задачи по теме «Решение неравенств методом интервалов»

Задание №1 . Решить неравенство

Решение:

6-2х-6-3х-х=0

-6х=0

4. На координатной прямой изобразим нули функции. Получили два промежутка

5. Определяем знак функции на каждом из полученных интервалов подстановкой в выражении функции какого-либо значения из соответствующего интервала: если х=-4, то

6. выберем для ответа нужные интервалы в соответствии со знаком неравенства.

Задание №2. Решить неравенство

Решение:

Решим неравенство методом интервалов.

Рассмотрим функцию f(x)=

и найдем множество значений х, при которых

1) Найдем

2) Найдем нули функции и точки, в которых функция не определена:

х-4х²=0

х-1≠ 0

х=0

х=1/4

х≠1

3)На координатной прямой изобразим нули функции и точки, в которых функция не определена. Получили четыре промежутка.

4)Определяем знак функции на каждом из полученных интервалов подстановкой в выражении функции какого-либо значения из соответствующего интервала.

5)выберем для ответа нужные интервалы в соответствии со знаком неравенства.

Ответ: (-∞;0] [1/4;1)

Задание №3. Решить неравенство .

Решение:

Рассмотрим функцию f(x)=x²(2x+1)(x-3) и найдем множество значений х , при которых

1)D(f)=R

2) Найдем нули функции:x²(2x+1)(x-3)=0

х²=0 2х+1=0 х-3=0

х₁=0 х₂=- х₃=3

3) На координатной прямой изобразим нули функции Получилось четыре интервала.

4) Определяем знак функции на каждом из полученных интервалов подстановкой в выражении функции какого-либо значения из соответствующего интервала.

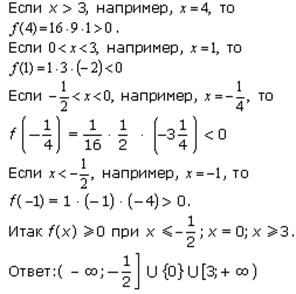
Задание №4. Решить неравенство

Решение:

Воспользуемся методом интервалов. Рассмотрим функцию f(x)=(3-x)log₃(x+5)

и найдем множество значений х , при которых

1) Найдем D(f). Т.к. D(log_a)=R₊, то x+5 >0; x >-5.

2) Найдем нули функции:(3-x)log₃(x+5)=0

Произведение равно нулю, если хотя бы один из множителей равен нулю, а другие при этом не теряют смысла.

а) 3-x=0, x=3 , при этом определен второй множитель log₃8.

б) log₃(x+5)=0, x+5=1, x=-4.

3) Отметим нули функции на координатной прямой

Ответ: (-5;4] [3;+ ∞]

Приложение №5

Задания по теме «Модуль числа»

Задание №1. Решить уравнение |х-5|=4.

Решение:

Исходя из определения модуля | f(x) |= а, f(x)=а, если f(x)˃0

f(x)=-а , если f(x)˂0 произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х₁=9, х₂=1.
Ответ: 9; 1.

Обобщение: | f(x) |= а ˂=˃ а≥0

f(x)=а

f(x)=-а

Задание №2 Решить уравнение |2-х|=2х+1.
Решение:

Прежде всего, следует установить область допустимых значений. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом необходимо найти область допустимых значений – это промежуток [-½; +∞).

Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит, является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения.

Ответ: ⅓.

Обобщение: | f(x) |=g(х) ˂=˃ g(х)≥0

f(x) =g(х)

f(x) = -g(х)

Задание №3 Решите уравнение: |х+3|=|2х-1|. В ответе указать целый корень.

Решение:

1 способ:

1) Чтобы решить такого вида уравнение необходимо знать:

| f(x) |=|g(х)| ˂=˃ f(x) =g(х)

f(x) = -g(х)

2) Исходя из этого имеем:

|х+3|=|2х-1|˂=˃ х+3=2х-1

х+3=-2х+1

3) Решим полученные уравнения:

х+3=2х-1 х+3=-2х+1

х=4 х=

Ответ: 4.

2 способ:

Решение:

Для решения уравнения воспользуемся методом возведения обеих частей уравнения в квадрат.

1) (|х+3|)²=(|2х-1|)²

2) Воспользуемся формулой сокращенного умножения а²- в²=(а-в)(а+в) и получим: (х+3-2х+1)(х+3+2х-1)=0

3) Решим данное уравнение и получим его корни: х=4; х=

4) В ответе укажем только целый корень.

Ответ: 4

Задачи типа №7. Приложение №6

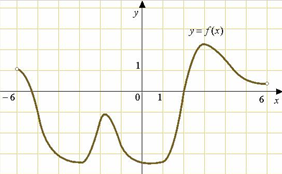
Задача1. На рисунке изображен график функции у=f(х),определенной на интервале (-6;6). Найдите количество точек, в которых касательная к графику функции параллельна прямой у=-5.

Теоретическая основа:

· уравнение прямой;

· уравнение касательной;

· условие параллельности двух

прямых.

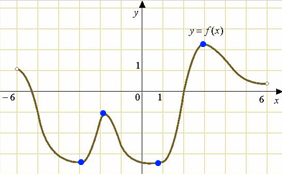Решение: Так как прямая у=-5 (у=kx+b, k=0) имеет коэффициент k равный нулю, то и угловой коэффициент касательной (y=f¹(x₀)(x-x₀)-f(x₀), k=f¹(x₀)) тоже должен быть равен нулю ( условие параллельности двух прямых). Считаем количество экстремумов (точек максимума и минимума) функции.

В данном случае их количество равно 4 (синие точки).

Ответ:4.

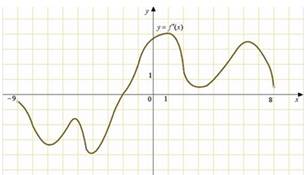Задача 2. На рисунке изображен график у=f ¹(х) - производной функции f(х), определенной на интервале (-9;8).В какой точке отрезка[-8,-4] f(х) принимает наименьшее значение.

Теоретическая основа:

· достаточный признак возрастания и убывания функции с помощью производной;

· правило отыскания наибольшего и наименьшего значения непрерывной на отрезке функции.

Решение: На отрезке [-8;-4] график производной функции лежит ниже оси ОХ, значит график функции убывает, и наименьшее значение график принимает в точке -4 (в правом конце указанного промежутка).

Ответ: -4.

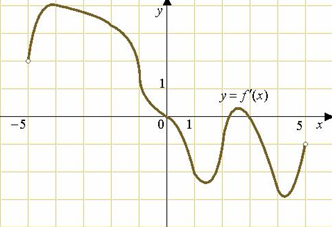Задача 3. На рисунке изображен график производной функции f(х), определенной на интервале (-5;5). Найдите количество точек экстремума функции f(х) на отрезке [-4;4]

Теоретическая основа:

· достаточный признак возрастания и убывания функции с помощью производной:

ü Функция убывает на промежутке, если на этом промежутке f¹(x)˂0, т.е. график производной функции расположен ниже оси ОХ.

ü Функция возрастает на промежутке, если на этом промежутке f¹(x)˃0, т.е. график производной функции расположен выше оси ОХ.

· признаки максимума и минимума функции:

ü Если в точке х₀производная меняет знак с плюса на минус, то х₀ есть точка максимума.

ü Если в точке х₀производная меняет знак с минуса на плюс, то х₀ есть точка минимума. [21]

Решение:

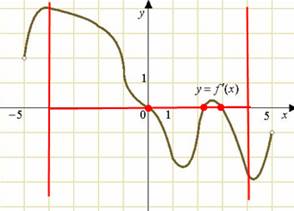Рассмотрим отрезок от -4 до 4:

Количество точек экстремума - есть количество точек пересечения графика производной функции с осью ОХ. Таких точек три.

Ответ: 3

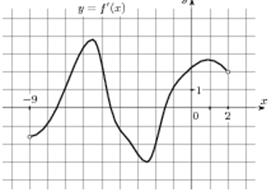Задача 4. На рисунке изображен график у=f ¹(х) - производной функции f(х), определенной на интервале (-9;2). Найдите промежутки убывания функции f(х). В ответе укажите сумму целых точек, входящих в эти промежутки.

Теоретическая основа:

Функция убывает на промежутке, если на этом промежутке f¹(x)˂0, т.е. график производной функции расположен ниже оси ОХ.

Решение:

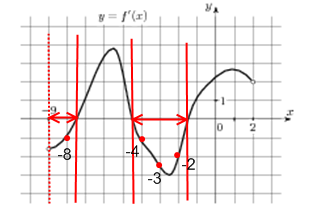В нашем случае таких промежутка два: первый содержит целую точку -8, а второй содержит целые точки -4, -3, -2.

Найдем их сумму: -8-4-3-2=-17

Ответ: -17

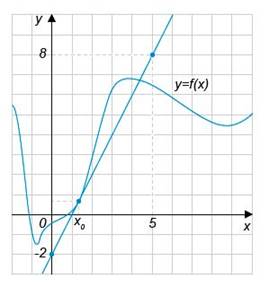Задача 5. На рисунке изображен график функции у=f(х) и касательная к нему в точке с абсциссой х. Найдите значение производной функции f(х) в точке х_0.

Решение: Данную задачу можно решить двумя способами:

1. Геометрический смысл производной

2. По определению производной.

1 способ: Значение производной в точке x₀ совпадает с тангенсом угла наклона (он же – угловой коэффициент) касательной в точке x₀. Эта касательная изображена на рисунке. Вычисление углового коэффициента облегчается тем, что касательная проходит через два узла целочисленной решетки. Эти точки выделены на рисунке жирным и имеют координаты (0, -2) и (5,8) соответственно. Стороны прямоугольника, у которого эти точки являются противоположными вершинами, имеют длины 5 – 0 = 5 (горизонтальная) и 8 – (-2) = 10 (вертикальная). Тангенс угла наклона касательной t = 10/5 = 2

2 способ:

1) По определению производной f^!(х)=

2) По графику находим координаты точки А(0;-2) и точки В(5;8); значит х₁=0, х₂=5, у₁=-2, у₂=8

3) Подставим в формулу значения переменных и получим

f^!(х)= =2

Ответ: 2

Приложение №7

Группа задач типа №11.

Задача 1. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за 3 дня?

После зачтения задачи проводится анализ.

o Какие величины содержатся в задаче?

o Как связаны между собой производительность труда, время и объем выполненных работ?

o Сколько можно выделить в задаче различных ситуаций (событий, случаев, фактов)?

o Какие величины известны в каждой ситуации?

o Какая неизвестная величина в задаче является искомой?

Выполненный анализ позволяет осуществить запись условий и требования задачи в виде таблицы.

Решение: Составим таблицу:

	V (раб./день)	T (дней)	A(раб.)
1 рабочий		х	1
2 рабочий		у	1
вместе		12	1

По условию вместе рабочие делают часть работы, составим первое уравнение системы + =.

Для второго уравнения нужна еще одна таблица:

	V(раб./день)	T(дней)	A(раб.)
1 рабочий		2
2 рабочий		3

Составим систему уравнений с учетом данных второй таблицы:

+ = + = + = = х = =20

= = = = у = =30

Ответ: 20

Задача2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.

Решение: Составим таблицу:

	V (км/ч)	t (ч.)	S (км)
Из А в В	х		70
Из В в А	х+3		70

По условию задачи велосипедист сделал остановку на 3 часа. Составим уравнение: + 3 = . умножим обе части уравнения на х(х+3)

70х+3х²+9х=70х+210 перенесем все слагаемые в одну часть, приведем подобные слагаемые и запишем полученное квадратное уравнение: х²+3х-70=0, корнями которого являются числа х₁=7, х₂=-10.

Корень -10 не удовлетворяет условию задачи, следовательно, 7 км/ч – скорость велосипедиста.

Ответ: 7.

Задача3. Из пункта А в пункт В вышел товарный поезд. Спустя 3 часа вслед за ним вышел пассажирский поезд, скорость которого на 30 км/ч больше скорости товарного поезда. Через 15 часов после своего выхода пассажирский поезд оказался впереди товарного на 300 км. Определите скорость товарного поезда.

Решение: Составим таблицу:

	Скорость (км/ч)	Время (ч.)	Расстояние(км.)
Товарный поезд	Х	(15+3)	18х
Пассажирский поезд	(х+30)	15	15(х+30)

Так как пассажирский поезд прошел на 300 км больше товарного, получаем уравнение: 15(х+30)-18х=300

15х+450-18х=300

3х=150; х=50 км/ч

Ответ: 50

Задача4. Сплавили 300 г сплава олова и меди, содержащего60% олова, и 900 г сплава олова и меди, содержащего 80% олова. Сколько процентов олова в получившемся сплаве?

Решение:

Масса олова в первом сплаве равна 0,6*300=180 г

Масса олова во втором сплаве равна 0,8*900=720 г

Масса олова в новом сплаве равна 180+720=900 г

Масса нового сплава равна 300+901200 г

Процентное содержание олова в новом сплаве равно =75%

Ответ: 75.

Приложение №8

Группа задач типа №12.

Задача 1. Найдите наибольшее значение функции y=9cosx+16x−8 на отрезке [−3π/ 2 ;0]

Решение:

1. Найдем производную функции y=9cosx+16x−8

f ′ (x)=9⋅(−sinx)+16=−9sinx+16

2. Найдем критически точки функции: f ′ (x)=0

−9sinx+16=0
sinx=16/ 9
Это уравнение не имеет решений, так как функция синус принимает значение от -1 до 1.
У функции f(x)=9cosx+16x−8 нет критических точек.

3. Найдем значение f(x) на концах отрезка [−3π/ 2 ;0] и выберем наибольшее.
f(−3π/ 2 )=9cos(−3π/ 2 )−16⋅3π 2 −8=−8(3π+1)⇒f(−3π /2 )<0.
f(0)=9cos0+16⋅0−8=9−8=1⇒f(0)>0
f(0)>f(−3π/ 2 ).
Наибольшее значение функции f(x)=9cosx+16x−8 на отрезке [−3π/ 2 ;0] равно 1.

Ответ: 1.

Задача 2. Найдите наибольшее значение функции на отрезке

Решение.

Найдём производную заданной функции:

Из уравнения найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции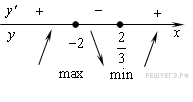

На отрезке [−2; 0] функция убывает, поэтому она достигает своего наибольшего значения в точке x = −2. Найдём это наибольшее значение:

Ответ: 1.

В итоге работы с заданиями типа №12 учащиеся должны усвоить алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке [а;в]:

1) Найти область определения функции и проверить содержится ли в ней отрезок [а;в].

2) Найти производную данной функции.

3) Решить уравнение f¹(x)=0 и отобрать только те корни уравнения, которые принадлежат отрезку [а;в]

4) Вычисляем значения функции в отобранных стационарных точках (если таковые имеются), а также при x = a и x = b.

5) Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми.

Данный алгоритм будет служить основой для решения других задач на нахождение наибольшего или наименьшего значения функции на отрезке.

Приложение №9

Задачи на отработку способов отбора корней.

При отборе корней в процессе решения тригонометрических уравнении обычно используют один из следующих способов:

● Арифметический способ:

а) решение двойного неравенства, относительно целочисленного п;

б) перебор значений целочисленного параметра и вычисление корней.

● Геометрический способ

а) изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений;

б) изображение корней на числовой прямой с последующим отбором с учетом

имеющихся ограничений.

Чтобы учитывать область допустимых значений учащиеся должны уметь решать простейшие тригонометрические неравенства с помощью тригонометрического круга и графиков тригонометрической функции.

Для повторения можно использовать следующие задания:

Задание №1. Решите неравенство .

Решение: Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит .

Для решением данного неравенства будут . Ясно также, что если некоторое число будет отличаться от какого-нибудь числа из указанного интервала на , то также будет не меньше . Следовательно, к концам найденного отрезка решения нужно добавить . Окончательно, получаем, что решениями исходного неравенства будут все .

Отве:. .

Другой подход решения тригонометрических неравенств: с помощью числовой прямой.

Задание №2 .Решить неравенство .

1 способ.

Решение: Рассмотрим график функции

Выберем из промежутка на оси значения аргумента , которым соответствуют точки графика, лежащие выше оси . Таким промежутком является интервал . Учитывая периодичность функции все решения неравенства можно записать так: .

Ответ. .

2 способ.

Решение: Используем тригонометрический круг.

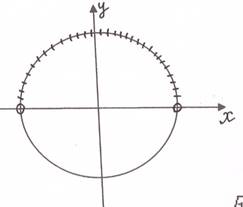
Задание №3. Решить уравнение

Решение. Данное уравнение равносильно следующей системе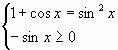

Далее имеем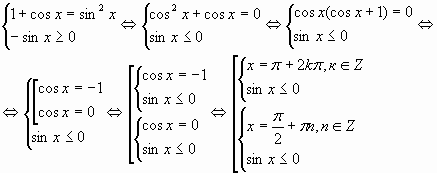

Рассмотрим окружность. Отметим на ней корни каждой системы и отметим дугой ту часть окружности, где выполняется неравенство

Получаем, что не может быть решением исходного уравнения.

Ответ:

Задание №4 . Решить уравнение 2sin ²x -3cosx – 3=0

Найти все корни уравнения, принадлежащие отрезку [π;3π].

Решение:

1) Воспользуемся основным тригонометрическим тождеством. Получим уравнение: 2(1- cos ²x)-3 cosx-3=0

2)Раскроем скобки: 2-2 cos ²x-3 cosx-3=0

3)Приведем подобные слагаемые: -2 cos ²x-3 cosx-1=0

4) Разделим все слагаемые уравнения на (-1): 2 cos ²x+3 cosx+1=0

5)Выполним замену cosx=а и получим квадратное уравнение: 2а²+3а+1=0

6)Решая данное уравнение получим корни: а₁=-1; а₂=-1/2

7)Вернемся к замене: cosx₁=-1 cosx₂=-

х₁=π+2πп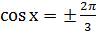

8) Проверим какие корни принадлежат отрезку [π;3π].

1) π≤ +2πп ≤ 3π

1≤ + 2п ≤3 ; ;

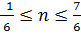п=1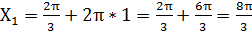

2) π≤ - +2πп ≤ 3π

1≤ - +2п≤ 3

≤ 2п≤ ; ≤ п ≤

п=1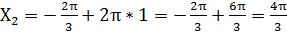

3) π ≤ π+2πп ≤ 3π

1 ≤ 1+2п ≤ 3

0 ≤ 2п ≤ 2 ; п=1; п=0

п=1

п=0

Ответ: х₁= ; х₂= ; х₃=; х₄=

Приложение №10

Задачи типа №13.

Задача 1. Решите уравнение . Укажите его корни, принадлежащие отрезку [-π;]
Решение.

1) Данное уравнение является однородным второй степени. Разделим каждое слагаемое уравнения на ()

2) Получим: tg²х-2 tg х-3=0

3) Сделаем замену: tg х=а

4) Получим квадратное уравнение а²-2а-3=0, корнями которого являются числа 3 и -1

5) Вернемся к замене и получим tg х=3 и tg х=-1

х=arctg 3+πп и х=- +πп

6) С помощью числовой прямой определим какие корни принадлежат промежутку [-π;]

Ответ: х₁=- ; х₂=arctg 3-π; х₃=arctg 3

Задача 2. Решите уравнение -2х)=0 и укажите корни, принадлежащие промежутку [-π;]

Решение:

1) С помощью формул приведения получим:

2) С помощью основных тригонометрических формул получим: -2=0

3) вынесем за скобки: ( - 2 )=0

4) Решим полученное уравнение: =0 или ( - 2 )=0

х=πk, kΖ; cos²х=

х=+, kΖ

5) Отметим решения на единичной окружности.

6) Выберем корни, которые принадлежат промежутку [-π;] : -π; -; -; 0; .

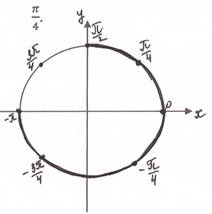
Ответ: -π; -; -; 0; .

Задача 3. Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку

Решение.
Решим уравнение:

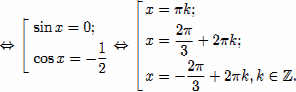
с помощью числовой окружности отберём корни, принадлежащие отрезку .

Это числа : .

Ответ:
а) .
б) .

Приложение №11

Факультативный курс по математике «Решение уравнений с модулем»

Пояснительная записка

Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.

Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы и на ЕГЭ.

Владение решением уравнений и неравенств с модулем будет служить пропедевтикой изучения математического анализа в ВУЗе. В частности таких понятий как непрерывность функции, предел функции, производная и др.

Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Это и позволит сделать элективный курс «Решение уравнений с модулем».

Курс рассчитан на учащихся 9-11 классов общеобразовательных школ, проявляющих интерес к изучению математики.

Курс позволит школьникам систематизировать, расширить и укрепить знания, связанные с абсолютной величиной, подготовиться для дальнейшего изучения тем, использующих это понятие, научиться решать разнообразные задачи различной сложности, способствует выработке и закреплению навыков работы на компьютере.

Учителю курс поможет наиболее качественно подготовить учащихся к математическим олимпиадам, сдаче ЕГЭ и экзаменов при поступлении в вузы.

Программа факультативного курса предполагает знакомство с теорией и практикой рассматриваемых вопросов и рассчитана на 34 часа: 7,5 часов лекций и 26,5 часов практических занятий.

Содержание курса состоит из восьми разделов, включая введение и итоговое занятие. Учитель, в зависимости от уровня подготовки учащихся, уровня сложности изучаемого материала и восприятия его школьниками, может взять для изучения не все темы, увеличив при этом количество часов на изучение других. Учитель также может изменить уровень сложности представленного материала.

Программа содержит темы творческих работ и список литературы по предложенным темам.

В процессе изучения данного курса предполагается использование различных методов активизации познавательной деятельности школьников, а также различных форм организации их самостоятельной работы.

Результатом освоения программы курса является представление школьниками творческих индивидуальных и групповых работ на итоговом занятии.

Цели курса:

обобщение и систематизация, расширение и углубление знаний по теме «Абсолютная величина»; обретение практических навыков выполнения заданий с модулем; повышение уровня математической подготовки школьников.

Задачи курса:

· вооружить учащихся системой знаний по теме «Абсолютная величина»;

· сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;

· подготовить учащихся к ЕГЭ;

· сформировать навыки самостоятельной работы, работы в малых группах;

· сформировать навыки работы со справочной литературой, с компьютером;

· сформировать умения и навыки исследовательской работы;

· способствовать развитию алгоритмического мышления учащихся;

· способствовать формированию познавательного интереса к математике.

Требования к уровню усвоения учебного материала

В результате изучения программы факультативного курса «Решение уравнений с модулем» учащиеся получают возможность знать и понимать:

· определение абсолютной величины действительного числа;

· основные операции и свойства абсолютной величины;

· правила построения графиков уравнений (в т.ч. функций), содержащих знак абсолютной величины;

· алгоритмы решения уравнений, неравенств, систем уравнений и неравенств, содержащих переменную под знаком модуля.

Уметь:

· применять определение, свойства абсолютной величины действительного числа к решению конкретных задач;

· читать и строить графики функций, аналитическое выражение которых содержит знак абсолютной величины;

· решать уравнения, неравенства, системы уравнений и неравенств, содержащих переменную под знаком модуля.

Содержание курса

(1 ч в 2 недели, всего 17 ч)

1. Введение (1 ч).

Цели и задачи факультативного курса. Вопросы, рассматриваемые в курсе и его структура. Знакомство с литературой, темами творческих работ. Требования, предъявляемые к участникам курса. Аукцион «Что я знаю об абсолютной величине?».

2. Абсолютная величина действительного числа а (2 ч).

Абсолютная величина действительного числа а. Модули противоположных чисел. Геометрическая интерпретация понятия модуля а. Свойства модуля. Операции над абсолютными величинами. Упрощение выражений, содержащих переменную под знаком модуля. Применение свойств модуля при решении задач.

3. Графики уравнений (в т.ч. функций), аналитическое выражение которых содержит знак абсолютной величины (3 ч).

Правила и алгоритмы построения графиков уравнений, аналитическое выражение которых содержит знак модуля. Графики уравнений

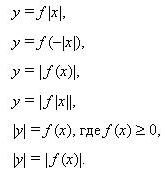
Графики некоторых простейших функций, заданных явно и неявно, аналитическое выражение которых содержит знак модуля. Графики уравнений (в т.ч. функций), аналитическое выражение которых содержит знак абсолютной величины в олимпиадных заданиях.

4. Уравнения, содержащие абсолютные величины (8 ч).

Основные методы решения уравнений с модулем. Раскрытие модуля по определению, переход от исходного уравнения к равносильной системе, возведение в квадрат обеих частей уравнения, метод интервалов, графический метод, использование свойств абсолютной величины. Уравнения вида

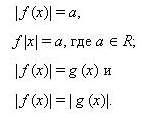
Метод замены переменных при решении уравнений, содержащих абсолютные величины. Метод интервалов при решении уравнений, содержащих абсолютные величины. Уравнения вида

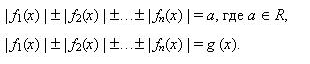
Способ последовательного раскрытия модуля при решении уравнений, содержащих «модуль в модуле». Графическое решение уравнений, содержащих абсолютные величины. Использование свойств абсолютной величины при решении уравнений. Уравнения с параметрами, содержащие абсолютные величины. Защита решенных олимпиадных заданий.

5. Модуль в заданиях ЕГЭ ( 3 часа)

Учебно-тематический план.

*№ занятия*	*Тема занятия*	*Основная цель занятия*	*Вид занятия*
1.	*Введение*	Познакомить ребят с курсом, дать историческую справку о введении термина “модуль” и “знак модуля; познакомить ребят с темами творческих работ.	Лекция
	*Абсолютная величина действительного числа. (2часа)*
2	Абсолютная величина действительного числа. Модули противоположных чисел. Геометрическая интерпретация понятия модуля а.	Систематизировать и обобщить знания обучающихся по теме “Абсолютная величина”, полученные ими в 6 и 8 классах; рассмотреть геометрический смысл абсолютной величины.	Изучение нового материала. Практикум.
3.	Свойства модуля. Операции над абсолютными величинами.	Рассмотреть основные свойства модуля.	Изучение нового материала. Практикум
	Графики уравнений, аналитическое выражение которых содержит знак абсолютной величины (3 часа).
4.	Правила и алгоритмы построения графиков функций, содержащих знак модуля.	Рассмотреть основные правила построения графиков функций, содержащих модуль.	Изучение нового материала
5.	Построение графиков вида	Научить обучающихся строить графики вида	Практикум
6.	Построение графиков вида	Научить обучающихся строить графики вида	Практикум
	*Уравнения, содержащие абсолютные величины (8 часов).*
7.	Решение уравнений вида \|f(x)\|=а; Решение уравнений вида \|f(x)\|= g (x);		Практикум
8.	Решение уравнений вида \|f(x)\|= \|g(x)\|		Практикум
9.	Метод замены переменных при решении уравнений с модулем.		Изучение нового материала. Практикум
10.	Метод интервалов при решении уравнений с модулем.		Практикум
11.	Графический метод решения уравнений с модулем.		Практикум
12.	Решение уравнений вида		Изучение нового материала. Практикум
13.	Решение уравнений, содержащих абсолютную величину различными способами.		Практикум
14	Решение дрорбно-рациональных уравнений, содержащих модуль.		Изучение нового материала. Практикум
	*Модуль в заданиях ЕГЭ (3 часа)*
15.	Модуль в заданиях ЕГЭ типа С1		Практикум
16.	Модуль в заданиях ЕГЭ типа С5		Практикум
17.	Итоговое занятие. Защита ученических проектов и творческих работ.

Разработка занятия факультативного курса

«Решение уравнений с модулем»

по теме: «Решение уравнений вида $|f(x)| = g(x)\Leftrightarrow \begin{cases} g(x)\geqslant 0 \\ \left[\begin{array}{l}f(x) = g(x) \\ f(x)=-g(x)\end{array}\right. \end{cases}$ различными способами.»

Тема: «Решение уравнений, содержащих абсолютную величину различными способами».

Обучающая цель: 1. Сформировать умения решать уравнения с модулем различными способами.

2. Формировать представление о методах математики, как науки (общекультурная компетенция).

Развивающая цель: Развивать:

1. умения сравнивать, анализировать, строить аналогии (учебно-познавательная компетенция);

2.умение находить различные способы решения одного уравнения, содержащего абсолютную величину;

3. умение ставить цель и планировать деятельность, реализовывать план (учебно-познавательная компетенция);

4. умение слушать (коммуникативная компетенция).

Воспитательная цель: 1. Развивать навыки контроля и самоконтроля (компетенция личностного самосовершенствования).

2. Воспитывать ответственность (социально-трудовая компетенция).

Тип занятия: практическая работа.

Ход занятия

Считается, что чем больше способов решения существует у задачи, тем она интереснее с математической точки зрения. Поэтому уравнения с модулями можно смело назвать интересными. Рассмотрим пример.

1. Решить уравнение: (разобрать пример)

$|2x+1|=2x^2+1.$

Решение. Постараемся найти как можно большее количество решений данного уравнения.

Способ №1. «Возведение обеих частей уравнения в квадрат»

Решение :

1)Возведем обе части уравнения в квадрат.

$|2x+1|^2=(2x^2+1)^2\Leftrightarrow$

$4x^2+4x+1=4x^4+4x^2+1\Leftrightarrow$

$4x^4-4x=0\Leftrightarrow x(x^3-1) = 0\Leftrightarrow \left[\begin{array}{l}x=0,\\ x=1.\end{array}\right.$

1) Путем прямой подстановки в исходное уравнение проверим нет ли посторонних корней.

а) если х=0, то |2*0+1|=1; |1|=1

б) если х=1, то |2*1+1|=3; |3|=3

3) Убедились, что посторонних корней нет.

Ответ: 0; 1.

Способ №2. «Снятие модуля с помощью числовой прямой».

1) Для решения данным методом потребуется найти значение переменной при котором подмодульное выражение обращается в ноль: $\Leftrightarrow x = -\frac{1}{2}.$

2) Наносим данную точку на числовую прямую и определяем знаки подмодульного выражения на полученных промежутках.

2) Раскроем знак модуля на каждом промежутке в соответствии с полученными данными:

при $x\in\left(-\mathcal{1};-\frac{1}{2}\right]$ подмодульное выражение отрицательно, и модуль раскрывается со знаком минус: или Дискриминант этого квадратного уравнения отрицателен, корней нет.
при $x\in\left(-\frac{1}{2};+\mathcal{1}\right)$ подмодульное выражение положительно, и модуль раскрывается со знаком плюс:

2х(х-1)=0

х=0 х=1

3) Проверим все ли полученные корни принадлежат данному промежутку. Убедились, что корни уравнения и принадлежат промежутку $x\in\left(-\frac{1}{2};+\mathcal{1}\right)$

Ответ: 0; 1.

Способ №3. «Замена уравнения смешанной системой».

1) Известно, что:

$|f(x)| = g(x)\Leftrightarrow \begin{cases} g(x)\geqslant 0 \\ \left[\begin{array}{l}f(x) = g(x) \\ f(x)=-g(x)\end{array}\right. \end{cases}$

2) Раскроем модуль: 2х² +1≥0

2х+1=2х² +1

2х+1= - (2х² +1)

1) Неравенство выполняется при любом значении Следовательно, в составе системы на него вообще можно не обращать внимания.

2) Решим совокупность двух упавнений:

$\left[\begin{array}{l}2x+1 = 2x^2+1, \\ 2x+1 =-2x^2-1 \end{array}\right.\Leftrightarrow \left[\begin{array}{l} x=0, \\ x=1.\end{array}\right.$

Ответ: 0;

2. Упражнения для фронтальной и самостоятельной работы:

а) |2х-1|=х-3 д) х+|х+1|=11

б) |х-3|=х-2 е) х-4-|2-х|= -2

в) 3х+1=|х-4 ж) |х+1| - 2=3

г) |3х+1|+х=9

Разработка занятия факультативного курса

«Решение уравнений с модулем»

тема: «Решение дрорбно-рациональных уравнений, содержащих модуль»

Обучающая цель: 1. Сформировать умение решать дробно-рациональные уравнения, содержащие модуль.

2. Формировать представление о методах математики, как науки (общекультурная компетенция).

Развивающая цель: Развивать 1. умения сравнивать, анализировать, строить аналогии (учебно-познавательная компетенция);

2. умение ставить цель и планировать деятельность, реализовывать план (учебно-познавательная компетенция);

3. умение слушать, работать в паре (коммуникативная компетенция).

2. Воспитывать ответственность (социально-трудовая компетенция).

Ход занятия:

При решении уравнений, содержащих переменную под знаком модуля, чаще всего применяются следующие методы:

1)раскрытие модуля по определению;

1) метод интервалов;

2) возведение обеих частей уравнения в квадрат.

Задание №1. Решить уравнение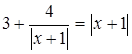

Решение:

если f (x) >0

если f (x) =0

если f (x) <0

Решим данное уравнение методом раскрытия модуля по определению:

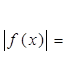
1) Раскроем модуль по определению:

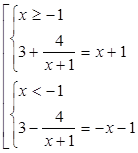
2) Решим каждую систему в совокупности отдельно:

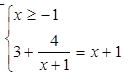или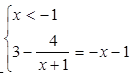

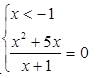
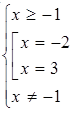
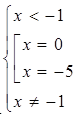
3) Выберем решение каждой из систем совокупности:

х=3; х=-5

Ответ: -5; 3.

Задание №2. Решить уравнение: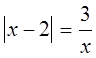

Решение:

Если˂0, то данное уравнение решений не имеет, так как |х-2|˃0 при любых значениях х.

Если ˃ 0 (х˃0), то обе части уравнения неотрицательны.

Воспользуемся методом возведения обеих частей уравнения в квадрат.

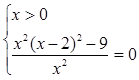
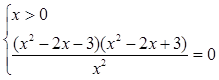
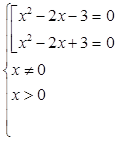
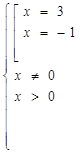х=3

Ответ: 3.

2. Упражнения для самостоятельной работы:

а)

б) |х+3|=

в) |х+4|=

Дидактические материалы для проведения занятия по теме «Модуль в заданиях ЕГЭ типа №18».

Задание №1. Найдите все значения a, при каждом из которых уравнение x² + (a + 4)² = | x + a + 4 | + | x – a – 4 | имеет единственный корень.

Решение:

При каждом конкретном значении параметра a функции f(x) = x² + (a + 4)² и g(x) = | x + a + 4 | + | x – a – 4 |, входящие в левую и правую части уравнения, являются четными, поскольку выполняются следующие условия:

1) они определены на всей числовой прямой (области определения симметричны относительно начала координат);

2) f(–x) = (–x)2 + (a + 4)2 = x2 + (a + 4)2 = f(x),

g(–x) = | –x + a + 4 | + | –x – a – 4 | = | x – a – 4 | + | x + a + 4 | = g(x).

Следовательно, если число x₀ — корень уравнения f(x) = g(x), то число –x₀также будет являться корнем этого уравнения. Условие единственности будет выполняться, если x = 0 — корень уравнения f(x) = g(x) и других корней нет.

Подставив в исходное уравнение значение x = 0,получим уравнение относительно параметра a:

(a + 4)² = | a + 4 | + | –a – 4 | ⇔ (a + 4)² – 2| a + 4 | = 0 ⇔

|а+ 4 | =0,

|а+ 4 |- 2= 0

Отсюда получаем три значения параметра:

a = –6, a = –4 и a = –2.

Пусть a = –6. Подставив a = –6 в исходное уравнение, получим:

х² + 4 = | x – 2 | + | x + 2 |.

Правая часть этого уравнения после раскрытия на промежутках модулей имеет вид:

-2х, если х˂ 2,

|х-2|+|х+2| = 4, если -2≤ х ≤ 2,

2х, если х≥ 2

Уравнения x² + 4 = –2x и x² + 4 = 2x не имеют корней, а уравнение x² + 4 = 4 имеет единственный корень x = 0, удовлетворяющий условию –2 ≤ x < 2.

Пусть a = –2. Подставив это значение параметра в исходное уравнение, получим:

х² + 4 = | x + 2 | + | x – 2 |.

Как только что было получено, это уравнение имеет единственный корень x = 0.

Пусть a = –4. Подставив это значение параметра в исходное уравнение, получим:

х² = 2| x | ⇔ |х|=0

|х| =2 ⇔ x = 0, x = –2, x = 2.

Значение a = –4 не соответствует условию задачи.

Ответ: –6; –2.

Задание №2. Найдите все значения a, при каждом из которых уравнение

4x – | 3x – | x + a | | = 9| x – 1 | имеет хотя бы один корень.

Решение:

Способ I.

Запишем уравнение в виде 9| x – 1 | – 4x + | 3x – | x + a | | = 0.

Функция f(x) = 9| x – 1 | – 4x + | 3x – | x + a | | непрерывна и

1) неограниченно возрастает при x ≥ 1, так как при любом раскрытии модулей имеем

f(x) = 9x – 9 – 4x 3x x a = kx + m, где k ≥ 9 – 4 – 4 = 1 > 0;

2) убывает при x ≤ 1, так как при любом раскрытии модулей имеем

f(x) = –9x + 9 – 4x 3x x a = kx + m, где k ≤ –9 – 4 + 4 = –9 < 0.

Следовательно, наименьшее значение функция f принимает при x = 1, и уравнение f(x) = 0 будет иметь корень тогда и только тогда, когда f(1) ≤ 0.

Решим это неравенство:

| 3 – | 1 + a | | ≤ 4, –4 ≤ 3 – | 1 + a | ≤ 4,

| 1 + a | ≤ 7, –7 ≤ 1 + a ≤ 7, –8 ≤ a ≤ 6.

Способ II.

Запишем уравнение следующим образом: | 3x – | x + a | | = 4x – 9| x – 1 |.

Раскрывая модули в выражении, стоящем в правой части уравнения, получим:

g (x)= 4х-9|х-1| = -5х+9, если х≥ 1

13х – 9, если х˂1

Для существования решения уравнения должно выполняться условие

g(x) ≥ 0˂=˃ .

На отрезке исходное уравнение равносильно совокупности двух уравнений:

3х- |х+а |= 4х- 9| х-1|

3х- |х+а |=- 4х+ 9|х- 1|,

| х+а|=-х+ 9|х- 1|

|х+а |= 7х- 9|х- 1|.

Раскрывая модули в правых частях уравнений совокупности, получим замкнутую ломаную, звенья которой — отрезки прямых, имеющих уравнения y = –2x + 9 (AD), y = 8x – 9 (CD), y = 16x – 9 (BA) и y = –10x + 9 (CB)

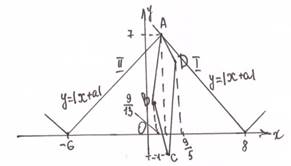
При каждом фиксированном значении параметра a график функции y_а(x) = | x + a | получается параллельным переносом графика функции

y = | x | вдоль оси Ox на –a единиц.

Имеется два критических положения графика функции y_а(x) = | x + a |. В обоих случаях он проходит через точку A(1; 7). Из условия y_а(1) = 7 получаем уравнение | 1 + a | = 7. Отсюда a₁ = –8 и a₂ = 6.

Соответственно, исходное уравнение будет иметь решение при –6 ≤ –a ≤ 8 или –8 ≤ a ≤ 6. При других значениях параметра a график функции

у_а(x) = | x + a | не будет иметь общих точек с ломаной AВСD.

Ответ: –8 ≤ a ≤ 6.

Задание №3. Найдите все значения а, при каждом из которых функция f(x)=х²-3|х-а²|-5х имеет более двух точек экстремума.

Решение:

При х ≥ а² f(x)=х²-8х+3а², поэтому график функции есть част параболы с ветвями, направленными вверх, и осью симметрии х=4.

При х ≤ а² f(x)=х²-2х-3а²,поэтому график функции есть част параболы с ветвями, направленными вверх, и осью симметрии х=1.

Все возможные виды графика функции f(x) показаны на рисунках.

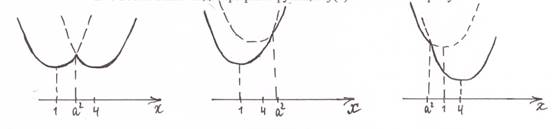
Обе параболы проходят через точку (а²; f(а²)).

Функция у= f(x) имеет более двух точек экстремума, а именно три, в единственном слечае: 1˂а²˂4, откуда 1˂|а|˂2.

Ответ: -2˂а˂-1; 1˂а˂2.

Дидактические материалы для проведения занятия по теме «Модуль в заданиях ЕГЭ типа №13».

Задание №1. Решите уравнение: | cos x | = sin x .

Решение. Из данного уравнения получаем равносильную систему

cos x = sin x tg х=

cos x = sin x ˂=˃ tg х=

sin х ≥0 sin х ≥0

х = +2п, п Z

˂=˃ х =- +2п, п Z

sin х ≥0

Так как функции tgx и sin x имеют общий наименьший положительный период

2 , то отбор корней проведем на тригонометрическом круге.

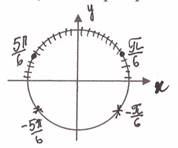
Ответ: х = +2k, +2п; k, п Z.

Задание №2. Решите уравнение: | cos x | = cos x + 2sin x .

Решение:

Рассмотрим две области на числовой прямой, на которых cos x ≥ 0 и cos x ˂ 0.

1) Пусть cos x ≥ 0 , тогда данное уравнение принимает вид:

cos x = cos x + 2sin x ˂=˃ sin x = 0 ˂=˃ x =π n, nZ.

Условию cos x ≥ 0 удовлетворяют только значения x = 2πn, nZ.

2) Для условия cos x ˂ 0 исходное уравнение перепишем в таком виде и решим его:

- cos x = cos x + 2sin x

- 2 cos x = 2sin x

sin x + cos x = 0

tgx +1 =0 ˂=˃ tgx =- 1 ˂=˃ х=+k; k Z.

Условию cos x ˂ 0 удовлетворяют только значения х=+k; k Z.

Ответ: 2π n, nZ; +k; k Z.

Задание №3. Найти все решения уравнения 2 cos 2 x -|1+2 1 на отрезке [0;4].

Решение:

1) Перепишем уравнение в виде |1+2=2 cos 2 x-1

2) Раскрывая знак модуля, получаем совокупность:

1+2≥0

1+2=2 cos 2 x-1

1+2˂0

-1-2=2 cos 2 x-1

3) Решим каждую систему совокупности отдельно:

1+2≥0 1+2˂0

1+2=2 cos 2 x-1 или -1-2=2 cos 2 x-1

а) Решим первую полученную систему в совокупности. С помощью формулы cos 2 x=1- 2 получим:

1+2≥0 ≥

2+=0 ˂=˃ ˂=˃ х=π n, nZ

= х=(-1)^k+k; k Z.

Точка +=≈3,55

б) Решим вторую полученную систему:

1+2˂0 ˂

-1-2=2 cos 2 x-1 ˂=˃ 2--1=0

Данная система решения не имеет.

Промежутку [0;4] принадлежат корни: 0; ; .

Ответ: 0; ; .

Задания для самостоятельной работы:

а) 2sin²x= ||

б) |х+3| cos х=х+3

Скачано с www.znanio.ru

Основные аспекты методики подготовки школьников к

Организация повторения курса математики………………

Результаты ЕГЭ по математике профильного уровня 2016 год 2015 год

Единый Государственный Экзамен по математике направлен на контроль сформированности у выпускников математических компетенций, предусмотренных требованиями

Но степень тревожности, напряжения у выпускников не снижается

ЕГЭ, я уделяю особое внимание.

ВУЗы, в которых предъявляются достаточно высокие требования к математической подготовке абитуриентов и студентов

Как правило, подготовка к ЕГЭ занимает у учащихся достаточно много времени и требует, кроме умственных усилий еще и решение организационных вопросов (подача заявлений на сдачу…

ЕГЭ, методические пособия, онлайн-тесты, тематические группы в социальных сетях частично облегчают труд учащегося при самоподготовке

В начале учебного года мы с ребятами разрабатываем программу подготовки к

Определить сколько времени имеет учащийся на подготовку к экзаменам

Единый государственный экзамен по мате матике, привнесенный в российское образо вательное пространство, имеет свои сильные и слабые стороны

Одновременно необходимо находить возможность восстанавливать базовые знания курса планиметрии (прямоугольный треугольник, решение треугольников, четырехугольники и т

Исходя из всего вышесказанного, учителю необходимо находить разнообразные методические приемы, использовать различные подходы и методы в обучении решению задач с модулем

Группы задач для подготовки к ЕГЭ

Приложение №7) · Задачи типа №12

Родители и некоторые педагоги полагают, что контролировать учителей и учеников надо в продолжение всего учебного года и так рационально поставить этот контроль, чтобы экзамены стали…

Необходимо работать над заданиями повышенной и высокой уровней сложности на дополнительных занятиях и факультативах

Алгебра и начала анализа: учеб

ПРИЛОЖЕНИЯ.

Приложение №2 Задачи для повторения или закрепления при изучении стереометрии

Треугольники АВС и АС

Через одну из скрещивающихся прямых провести плоскость, параллельную другой прямой

Если скрещивающиеся прямые принадлежат соответственно двум взаимно перпендикулярным плоскостям и одна из них перпендикулярна линии пересечения этих плоскостей, то провести через точку пересечения первой прямой…

На рисунке изображен график функции , определенной на интервале (−6; 8)

В ответе укажите сумму координат целых точек, входящих в эти промежутки

Задание №2. Решить неравенство

Ответ: (-∞;0] [1/4;1) Задание №3

Воспользуемся методом интервалов

Прежде всего, следует установить область допустимых значений

Ответ: 4. 2 способ: Решение:

Ответ :4. Задача 2. На рисунке изображен график у= f 1 (х) - производной функции f (х), определенной на интервале (-9;8)

Рассмотрим отрезок от -4 до 4:

Задача 5. На рисунке изображен график функции у= f (х) и касательная к нему в точке с абсциссой х

Приложение №7 Группа задач типа №11

По условию вместе рабочие делают часть работы, составим первое уравнение системы + =

Из А в В х 70

Задача4. Сплавили 300 г сплава олова и меди, содержащего60% олова, и 900 г сплава олова и меди, содержащего 80% олова

Найдем значение f ( x ) на концах отрезка [− 3 π/ 2 ; 0 ] и выберем наибольшее

Вычисляем значения функции в отобранных стационарных точках (если таковые имеются), а также при x = a и x = b

Решение: Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит

Решение: Используем тригонометрический круг

Ответ: Задание №4 . Решить уравнение 2sin 2 x -3cosx – 3 =0

Ответ: х 1 = ; х 2 = ; х 3 = ; х 4 =

Задача 2 . Решите уравнение -2х)=0 и укажите корни, принадлежащие промежутку [-π; ]

Решение. Решим уравнение: с помощью числовой окружности отберём корни, принадлежащие отрезку

ЕГЭ. Владение решением уравнений и неравенств с модулем будет служить пропедевтикой изучения математического анализа в

Цели курса: обобщение и систематизация, расширение и углубление знаний по теме «Абсолютная величина»; обретение практических навыков выполнения заданий с модулем; повышение уровня математической подготовки школьников

Введение (1 ч). Цели и задачи факультативного курса

Метод замены переменных при решении уравнений, содержащих абсолютные величины

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

10.08.2021

Основные аспекты методики подготовки школьников к ЕГЭ по математике в средней школе

Тема: «Решение уравнений, содержащих абсолютную величину различными способами».

Основные аспекты методики подготовки школьников к

Организация повторения курса математики………………

Результаты ЕГЭ по математике профильного уровня 2016 год 2015 год

Единый Государственный Экзамен по математике направлен на контроль сформированности у выпускников математических компетенций, предусмотренных требованиями

Но степень тревожности, напряжения у выпускников не снижается

ЕГЭ, я уделяю особое внимание.

ВУЗы, в которых предъявляются достаточно высокие требования к математической подготовке абитуриентов и студентов

ЕГЭ, методические пособия, онлайн-тесты, тематические группы в социальных сетях частично облегчают труд учащегося при самоподготовке

В начале учебного года мы с ребятами разрабатываем программу подготовки к

Определить сколько времени имеет учащийся на подготовку к экзаменам

Единый государственный экзамен по мате­ матике, привнесенный в российское образо­ вательное пространство, имеет свои сильные и слабые стороны

Группы задач для подготовки к ЕГЭ

Приложение №7) · Задачи типа №12

Необходимо работать над заданиями повышенной и высокой уровней сложности на дополнительных занятиях и факультативах

Алгебра и начала анализа: учеб

ПРИЛОЖЕНИЯ.

Приложение №2 Задачи для повторения или закрепления при изучении стереометрии

Треугольники АВС и АС

Через одну из скрещивающихся прямых провести плоскость, параллельную другой прямой

На рисунке изображен график функции , определенной на интервале (−6; 8)

В ответе укажите сумму координат целых точек, входящих в эти промежутки

Задание №2. Решить неравенство

Ответ: (-∞;0] [1/4;1) Задание №3

Воспользуемся методом интервалов

Прежде всего, следует установить область допустимых значений

Ответ: 4. 2 способ: Решение:

Ответ :4. Задача 2. На рисунке изображен график у= f 1 (х) - производной функции f (х), определенной на интервале (-9;8)

Рассмотрим отрезок от -4 до 4:

Задача 5. На рисунке изображен график функции у= f (х) и касательная к нему в точке с абсциссой х

Приложение №7 Группа задач типа №11

По условию вместе рабочие делают часть работы, составим первое уравнение системы + =

Из А в В х 70

Задача4. Сплавили 300 г сплава олова и меди, содержащего60% олова, и 900 г сплава олова и меди, содержащего 80% олова

Найдем значение f ( x ) на концах отрезка [− 3 π/ 2 ; 0 ] и выберем наибольшее

Вычисляем значения функции в отобранных стационарных точках (если таковые имеются), а также при x = a и x = b

Решение: Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит

Решение: Используем тригонометрический круг

Ответ: Задание №4 . Решить уравнение 2sin 2 x -3cosx – 3 =0

Ответ: х 1 = ; х 2 = ; х 3 = ; х 4 =

Задача 2 . Решите уравнение -2х)=0 и укажите корни, принадлежащие промежутку [-π; ]

Решение. Решим уравнение: с помощью числовой окружности отберём корни, принадлежащие отрезку

ЕГЭ. Владение решением уравнений и неравенств с модулем будет служить пропедевтикой изучения математического анализа в

Введение (1 ч). Цели и задачи факультативного курса

Метод замены переменных при решении уравнений, содержащих абсолютные величины

Единый государственный экзамен по мате матике, привнесенный в российское образо вательное пространство, имеет свои сильные и слабые стороны