ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ НЕРАВЕНСТВ. (11 кл.)

Конспект занятия  по теме:

ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ НЕРАВЕНСТВ.

11 кл  (Профильное обучение)

Аспенбетова Р.А.

«Основные методы решения сложных неравенств».

Цель занятия: обобщить, систематизировать и повторить умения и навыки решения алгебраических неравенств методом интервалов, изучить метод замены множителей.

Задачи :

— повторить и обобщить метод интервалов и метод сведения неравенств к совокупности неравенств;

-познакомить обучающихся с методом замены множителей, как эффективным способом решения целого класса неравенств.

— подготовка обучающихся к решению задач  повышенной степени сложности.

Оборудование: карточки, компьютер,экран  

Ход  занятия.

1.Организационный этап (1 мин).( проверка посещаемости, настрой на занятие)

2. Повторение теоретического материала

Вопросы: Какие методы решения неравенств знаете? Как найти ОДЗ,МЗФ?

Свойства неравенств с модулем)

3. Подготовка к  решению примеров( учитель обобщает)

Основными методами решения неравенств являются:

метод интервалов, метод сведения к совокупности систем, метод замены множителей. Сегодня мы повторим первые 2 метода и познакомимся с методом замены множителей, который можно использовать при решении сложных неравенств.

1) Метод интервалов в том числе и обобщённый, применяемый для решения любых неравенств, содержащих элементарные функции.

Вспомним алгоритм решения неравенств «методом интервалов» дляf(x)/g(x)˃0

а). Найти область определения левой части неравенства, корни числителя и знаменателя.

б). Нанести найденные корни числителя и знаменателя на числовую ось в пределах ОДЗ.

в). Определить знаки левой части неравенства на полученных промежутках.

г). Выяснить принадлежность концов полученных промежутков (критических точек) множеству решений неравенства.

д). Выбрать промежутки, соответствующие знаку неравенства, записать ответ.

Этап 4. Проверка усвоения и коррекция знаний.

Задание №1. Выполнить решение следующих неравенств с помощью «метода интервалов». После решения осуществляется проверка.

1). Решить неравенство: 

Корни числителя:      Корни знаменателя:    От  −1

Ответ: 

Задание №2. Решить неравенство: 

Корни числителя:    Корни знаменателя:     От  2

Ответ:         Задание №3. Решить систему неравенств:

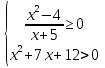          Ответ: 

Этап 5. Выполнить решение показательных и логарифмических неравенств из сборника заданий для подготовки к ЕГЭ. Для решения этих неравенств воспользуемся «методом интервалов» и методом сведения к совокупности систем. Решается неравенства №2.2 и №3.3 из сборника «Задача С3» под редакцией И.Н.Сергеева, В.А.Панферова. После выполнения заданий учащиеся анализируют методы решения, обобщают и систематизируют умения и навыки, которые можно применять при решении различных неравенств.

Этап 6. Углубление и расширение новых знаний.

Метод замены множителей.

Самым легким способом решения неравенств является способ решения рациональных неравенств методом интервалов, но не все неравенства имеют структуру, которая позволяет решать их этим методом. Поэтому цель сегодняшнего урока – изучить методы решения сложных неравенств (неравенства, содержащие логарифмические, показательные, иррациональные выражения и выражения с модулями) путем замены множителей. Идея этого метода заключается в том, что неравенства повышенной сложности сводятся к решению рациональных неравенств. Оказывается, достаточно широкий класс неравенств подобную попытку допускает. Как было сказано выше, решение неравенства – это объединение конечного числа непересекающихся промежутков. Их легко задать одним рациональным неравенством, что во многих ситуациях позволяет быстрее двигаться к ответу, а иногда получать более эффективные схемы решения типовых неравенств.

Вспоминаем определения возрастающей и убывающей функций.

Функция называется возрастающей (убывающей) на множестве M, если для любых  из множества М выполняется условие:  (.

Определения возрастающей и убывающей функций можно сформулировать по-другому. Функция называется возрастающей (убывающей) на множестве M, если для любых  из множества М выражения  и  имеют одинаковый (противоположный) знак.

Этот факт можно использовать при решении неравенств, в правой части которых стоит ноль. Можно в левой части (числителе и/или знаменателе левой части) заменить разность значений монотонной функции разностью значений аргумента. При этом, если функция возрастающая, то знак неравенства сохранится, а если функция убывающая, то знак неравенства поменяется на противоположный. Такой прием решения неравенств и называется методом замены множителей.

Замена множителей с показательными и логарифмическими выражениями.

Можно установить, что разность степеней по одному и тому же основанию всегда по знаку совпадает с произведением разности показателей этих степеней на отклонение основания степени от единицы. Другими словами, выражение вида  имеет тот же знак, что и выражение (f –g)(а – 1) при а> 0 (если а= 1, то выражения равны нулю). Сказанное равносильно тому, что разность логарифмов по одному и тому же основанию всегда по знаку совпадает с произведением разности чисел этих логарифмов на отклонение от единицы. Другими словами выражение вида (log_af – log_ag) имеет тот же знак (в области существования логарифмов) что и выражение (f-g)(α-1).

В частности, легко получить следующие полезные схемы неравенств:

Рассмотрим несколько неравенств.

№1. Решить неравенство 

В числителе левой части стоит разность значений возрастающей наR функции  .

В знаменателе тоже можно увидеть разность значений функции, если представить единицу как . Эта функция убывает на R. Значит, исходное неравенство равносильно неравенству

Решим полученное неравенство методом интервалов.   От

Корни числителя: 5;     Корень знаменателя: 0   Ответ: 

№ 2. Решить неравенство                

7. Этап закрепления новых знаний.

В качестве закрепления метода замены множителей решим неравенства из сборника заданий для ЕГЭ « Задача С3». Решение выполняется самостоятельно в парах. После чего следует воспроизведение правильного решения и комментариями.

8. Этап подведения итогов  занятия. Синквейн.

9. Информирования обучающихся о домашнем задании.  Задание на доске