Основные методы решения уравнений в целых числах

Министерство образования и науки Луганской Народной Республики

Отдел образования Администрации Славяносербского района ЛНР

ГУ ЛНР «Славяносербский райметодкабинет»

ГОУ ЛНР «Лотиковская СШ им. В.Лелеки»

Тематика задач

Основные методы решения уравнений

 в целых числах

Материал подготовили

Учителя математики

высшей квалификационной категории

Никифорова Инна Андреевна

Минько Лидия Анатольевна

2021 г.

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами занимались самые выдающиеся математики древности, например: греческий математик Пифагор (VI век до н.э.), александрийский математик Диофант (III век н.э.), П.Ферма(XVII в.), Л.Эйлер(XVIII век), Ж.Л.Лагранж(XVIII век), П.Дирихле(XIX век), К.Гаусс(XIX век), П.Чебышев(XIX в.) и многие другие.

Решение уравнений в целых числах является важной задачей и для современной математики.

Готовясь к олимпиадам, участвуя в олимпиадах, учащиеся встречаются с заданиями, в которых предлагаются  нелинейные уравнения. У ребят возникает желание узнать решаемы ли такие уравнения, и какие способы используются для их решения, все ли они имеют алгоритм решения, так как данная тема не достаточно глубоко представлена в школьном курсе математики.

Большинство методов решения таких уравнений основаны на теории делимости целых чисел, интерес к которой в настоящее время определяется бурным развитием информационных технологий. В связи с этим, учащимся старших классов будет небезынтересно познакомиться с методами решения некоторых уравнений в целых числах.

Отсюда определены цель и задачи работы:

– рассмотреть основные приемы и методы решения уравнений в целых числах;

– повысить уровень математической культуры учащихся;

– выработать навыки самостоятельной исследовательской работы в математике.

Мы представляем анализ уравнений в целых числах, классификацию данных уравнений по способам их решения, описание алгоритмов их решения, а также практические примеры применения каждого способа для решения уравнений в целых числах

Метод перебора вариантов.

Задача. В клетке сидят кролики и фазаны, всего у них 18 ног. Узнать, сколько в клетке тех и других?

Решение:

Составляется уравнение с двумя неизвестными переменными, в котором

 х – число кроликов, у – число фазанов:

4х + 2у = 18, или 2х + у = 9.

Выразим у через х: у = 9 – 2х

 Если х = 1, то у = 9 – 2 · 1 = 7

Если х = 2, то у = 9 – 2 · 2 = 5

Если х = 3, то у = 9 – 2 · 3 = 3

Если х = 4, то у = 9 – 2 ·4 = 1

Если х = 5, то у = 9 – 2 · 5 = -1– не удовлетворяет условию задачи.

Ответ: 1 кролик и 7 фазанов или 2 кролика и 5 фазанов или 3 кролика и 3 фазана или 4 кролика и 1 фазан.

Решить уравнение в целых числах у³ - х³ = 91.

Решение:

Запишем данное уравнение в виде

(y - x)(у² + xy +х²) = 91.

Так как у и х –целые, то целыми являются и выражения y – x и у² + xy +х²

 причем их произведение положительно. Учитывая, что у² + xy +х²

положительно при любых значениях переменных х, у, имеем у-х положительно.

Разложим число 91 на натуральные множители: 91 =1 91=7 13.

Тогда уравнение  равносильно совокупности систем уравнений:

 ;  ;  ;

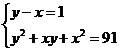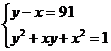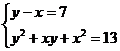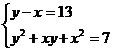
Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.

Ответ: (5; 6), (-6; -5),(-3; 4),(-4;3)

Решить уравнение в целых числах .

Решение:

Запишем в виде , ; .

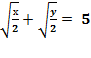x = 2m², y = 2n², m + n =5

Если m=0, n=5, то x=0, y=50 (0 ; 50)

Если m=5, n=0, то x=50, y=0 (50 ; 0)

Если m=1, n=4, то x=2, y=32 (2 ; 32)

Если m=4, n=1, то x=32, y=2 (32 ; 2)

Если m=3, n=2, то x=18, y=8 (18 ; 8)

Если m=2, n=3, то x=8, y=18 (8 ; 18)

Ответ: (0 ; 50), (50 ; 0), (2 ; 32), (32 ; 2), (18 ; 8), (8 ; 18)

Представление уравнения в виде суммы квадратов нескольких слагаемых, равной некоторому целому числу.

Решить в целых числах уравнение x² + y² – 2x + 6y + 5 = 0.

Решение:

Исходное уравнение можно переписать следующим образом:

(x – 1)² + (y + 3)² = 5.

Из условия следует, что (x – 1), (y + 3) – целые числа. Следовательно, данное уравнение эквивалентно следующей совокупности:

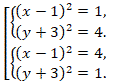
Теперь можно выписать всевозможные целые решения уравнения.

Ответ:  (5; 6); (-6; -5); (-3; 4); (-4;3).

Решить уравнение: 9x² + 4y² + 13 = 12(x + y).

Решение:

Группируем:

(9x² – 12x + 4) + (4y² – 12y + 9) = 0.

Теперь каждую скобку можно свернуть по формуле квадрата разности.

(3x – 2)² + (2y – 3)² = 0.

Сумма двух неотрицательных выражений равна нулю, только если 3x – 2 = 0 и 2y – 3 = 0.

А значит, x = 2/3 и y = 3/2.

Ответ: (2/3; 3/2).

Использование неравенств.

Решить в натуральных числах уравнение 5х+ 8у= 39.

Решение:

Для уменьшения перебора вариантов рассмотрим неравенства

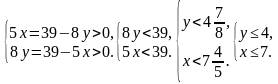
Проведем перебор по неизвестной у с учётом условия y ≤ 4. Предварительно выразим х:

Если у = 1, тоне является натуральным числом.

Если у = 2, тоне является натуральным числом.

Если у = 3, то

Если у = 4, тоне является натуральным числом.

Ответ: (3; 3).

Использование отношения делимости

Задача. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Указать все решения.

Решение:

Пусть х – количество контейнеров первого вида, у – количество контейнеров второго вида, тогда имеем уравнение:

Значит, разностьделится на 13.

Если не является натуральным числом.

Если не является натуральным числом.

Если

Если не является натуральным числом.

Если не является натуральным числом.

Если, но

Ответ: 12 контейнеров по 130 кг и 9 контейнеров по 160 кг.

Метод разложения на множители

Первоначальное уравнение путем группировки слагаемых и вынесения общих множителей приводится к виду, когда в левой части уравнения стоит произведение сомножителей, содержащих неизвестные, а справа стоит некоторое число. Рассматриваются все делители числа, стоящего в правой части уравнения. Проводится исследование, в котором каждый сомножитель, стоящий в правой части уравнения приравнивается к соответствующему делителю числа, стоящего в правой части уравнения.

Решить уравнение xy – 2 = 2x – y.

Решение:

Группируем слагаемые с целью разложения на множители:

(xy + y) – (2x + 2) = 0. Из каждой скобки вынесем общий множитель:

y(x + 1) – 2(x + 1) = 0;

(x + 1)(y – 2) = 0.

Имеем:

y = 2, x – любое действительное число или x = -1, y – любое действительное число.

Таким образом, ответом являются все пары вида (x; 2), x € R и (-1; y), y € R.

Ответ:(x; 2), x € R и (-1; y), y € R

Решить в целых числах уравнение x + y = xy.

Решение:

Перенесем все члены уравнения влево и к обеим частям полученного уравнения прибавим (–1): x + y – xy – 1 = – 1

Сгруппируем первое – четвертое и второе – третье слагаемые и вынесем общие множители, в результате получим уравнение: (x - 1)(y - 1) = 1

Произведение двух целых чисел может равняться 1 в том и только в том случае, когда оба этих числа равны или 1, или (–1).

Записав соответствующие системы уравнений и решив их, получим решение исходного уравнения.

Ответ: (0,0) и (2,2).

Доказать, что уравнение (x - y)³ + (y - z)³ + (z - x)³ = 30 не имеет решений в целых числах.

Решение:

1) Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:

(x - y)(y - z)(z - x) = 10

Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения  равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.

Ответ: уравнение не имеет решений в целых числах.

Решить в целых числах уравнение zt + t – 2z = 7.

Решение:

Исходное уравнение можно преобразовать к виду (z + 1) (t – 2) = 5.

Числа (z + 1), (t – 2) являются целыми, поэтому имеют место следующие варианты:

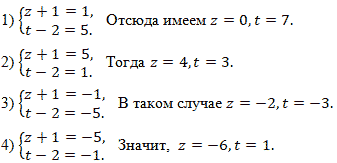
Итак, уравнение имеет ровно четыре целых решения

Ответ: z=0,t=7; z=4,t=3; z= -2,t= -3; z= -6,t=1.

Решить уравнение в целых числах х² + 23 = у²

Решение:

Перепишем уравнение в виде: у²- х²= 23, (у - х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

 ;  ;  ;  ;

Решая полученные системы, находим:

 ;  ;  ;  ;

Ответ: (-11;12);(11;12);(11;-12);(-11;-12).

Оценочный метод.

Решить уравнение  (x ² + 2x + 2)(y ² – 4y + 6) = 2.

Решение:

В каждой скобке выделим полный квадрат:

((x + 1) ² + 1)((y – 2) ² + 2) = 2. Оценим значение выражений, стоящих в скобках.

(x + 1) ² + 1 ≥ 1 и (y – 2) ² + 2 ≥ 2, тогда левая часть уравнения всегда не меньше 2. Равенство возможно, если:

(x + 1) ² + 1 = 1 и (y – 2) ² + 2 = 2, а значит x = -1, y = 2.

Ответ: (-1; 2).

Решить в целых числах уравнение (х² + 4)(у² + 1) = 8ху

Решение:

Заметим, что если  – решение уравнения, то  – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

,

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

,

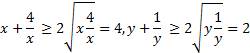тогда их произведение , значит,

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

Ответ: (2; 1); (-2; -1)

Выражение одной неизвестной переменной через другую

 и выделение целой части дроби.

Решить в целых числах уравнение xy + x + 2y = 1.

Решение:

Путём преобразований уравнение можно свести к следующему:

Данное преобразование не изменило ОДЗ неизвестных, входящих в уравнение, так как подстановка y = –1 в первоначальное уравнение приводит к абсурдному равенству –2 = 1. Согласно условию, x – целое число. Иначе говоря,  тоже целое число. Но тогда число  обязано быть целым. Дробь является целым числом тогда и только тогда, когда числитель делится на знаменатель. Делители числа 3: 1,3 –1, –3. Следовательно, для неизвестной возможны четыре случая: y = 0, y = 2, y = –2, y = –4. Теперь можно вычислить соответствующие значения неизвестной x.

Итак, уравнение имеет ровно четыре целых решения: (–5;0), (–5;2), (1;–2), (1;–4).

Ответ: (–5;0), (–5;2), (1;–2), (1;–4).

Решить уравнение в целых числах  х² + ху – у – 2 = 0.

Решение:

Выразим из данного уравнения у через х:

у(х - 1) =2 - х²,

Так как х, у – целые числа, то дробь  должна быть целым числом.

Это возможно, если х – 1 =

;  ;

 ; ;

Ответ: (0; -2); (2; -2).

Использование чётности/нечётности частей уравнения.

Решить в целых числах уравнение n(n + 1) = (2k + 1)!

Решение:

Число (2k + 1)! нечётно при всех неотрицательных значениях k согласно определению (при отрицательных k оно вообще не определено). С другой стороны, оно равно числу n(n + 1), которое чётно при всех целых значениях k. Противоречие

Ответ: уравнение не имеет решений в целых числах.

Метод испытания остатков.

Этот метод основан на исследовании возможных остатков левой и правой частей уравнения от деления на некоторое фиксированное натуральное число.Рассмотрим примеры, которые раскрывают сущность данного метода.

Решить в целых числах уравнение x² + 1 = 3y.

Решение:

Заметим, что правая часть уравнения делится на 3 при любом целом y. Исследуем какие остатки может иметь при делении на три левая часть этого уравнения.

x² при делении на 3 дает в остатке 0 или 1.Следовательно, левая часть на 3 не делится, притом, что правая часть уравнения делится на три при любых значениях переменной y. Следовательно, уравнение в целых числах решений не имеет.

Ответ: уравнение не имеет решений в целых числах.

Решить в целых числах уравнение 5^m = n² + 2.

Решение:

Если m = 0, то уравнение примет вид n² = –1. Оно не имеет целых решений. Если m < 0, то левая часть уравнения, а значит, и n, не будет являться целым числом. Значит, m > 0. Тогда правая часть уравнения (как и левая) будет кратна 5. Но в таком случае n² при делении на 5 должно давать остаток 3, что невозможно. Следовательно, данное уравнение не имеет решений в целых числах.

Ответ: уравнение не имеет решений в целых числах.

Решите в целых числах 3^х= 1 + y².

Решение:

Не сложно заметить, что (0; 0) — решение данного уравнения. Остаётся доказать, что других целых корней уравнение не имеет.

Рассмотрим случаи:

1) Если x∈N, y∈N, то З делится на три без остатка, а 1 + y²при делении на 3 дает остаток либо 1, либо 2. Следовательно, равенство при натуральных значениях х, у невозможно.

2) Если х— целое отрицательное число, y∈Z , тогда 0< 3^х< 1, а 1 + y² ≥ 0 и

равенство также невозможно. Следовательно, (0; 0) — единственное решение.

Ответ: (0; 0).

Доказать, что уравнение x² = 3y + 2 не имеет решений в целых числах.

Доказательство:

Рассмотрим случай, когда x, y ∈ N. Рассмотрим остатки от деления обоих частей на 3. Правая часть уравнения дает остаток 2 при делении на 3 при любом значении y. Левая же часть, которая является квадратом натурального числа, при делении на 3 всегда дает остаток 0 или 1. Исходя из этого получаем, что решения данного уравнения в натуральных числах нет.

Рассмотрим случай, когда одно из чисел равно 0. Тогда очевидно, решений в целых числах нет.

Случай, когда y - целое отрицательное не имеет решений, т.к. правая часть будет отрицательна, а левая - положительна.

Случай, когда x - целое отрицательное, также не имеет решений, т.к. попадает под один из рассмотренных ранее случаев ввиду того, что (-x)²= (x)².

Получается, что указанное уравнение не имеет решений в целых числах, что и требовалось доказать.

Решить уравнение в целых числа x² + y² = 4z - 1.

Решение:

Правая часть при делении на 4 дает остаток 3.

Левая часть при делении на 4 дает остаток: 0, если оба числа четные; остаток 1, если одно из чисел четное, а второе – нечетное; остаток 2, если оба числа нечетные. Поскольку левая и правая части имеют разные остатки, то ни при каких х, у,z уравнение решений не имеет.

Ответ: решений данное уравнение не имеет.

Решить в целых числах уравнение n² - 4y! = 3.

Решение:

Сначала перепишем исходное уравнение в виде n² = 4y! + 3. Если посмотреть на это соотношение с точки зрения теоремы о делении с остатком, то можно заметить, что точный квадрат, стоящий в левой части уравнения, даёт при делении на 4 остаток 3, что невозможно, так как точный квадрат при делении на 4 даёт в остатке либо 0, либо 1. Следовательно, исходное уравнение не имеет решений.

Ответ: решений данное уравнение не имеет

Решить уравнение в целых числах x ² + 5y ² = 20x + 2.

Решение:

Перепишем уравнение в виде x ² = -5y ² + 20x + 2. Правая часть полученного уравнения при делении на 5 дает в остатке 2. Следовательно, x ² не делится на 5. Но квадрат числа, не делящегося на 5, дает в остатке 1 или 4. Таким образом, равенство невозможно и решений нет.

Ответ: нет корней.

Решить в целых числах уравнение 1! + 2! + . . . + х! = у².

Решение:

Очевидно, что

если х = 1, то у² = 1,

если х = 3, то у² = 9.

Этим случаям соответствуют следующие пары чисел:

х₁ = 1, у₁ = 1;

х₂ = 1, у₂ = –1;

х₃ = 3, у₃ = 3;

х₄ = 3, у₄ = –3.

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

Решение уравнения как квадратного относительно

 одной из неизвестных.

Решить в целых числах уравнение 5x² – 3xy + y² = 4.

Решение:

Перепишем данное уравнение в виде 5x² – (3x)y + (y² – 4) = 0. Его можно рассмотреть как квадратное относительно неизвестной x. Вычислим дискриминант этого уравнения:

Для того чтобы уравнение имело решения, необходимо и достаточно, чтобы , то есть  Отсюда имеем следующие возможности для y:

Y = 0, y = 1, y = –1, y = 2, y = –2.

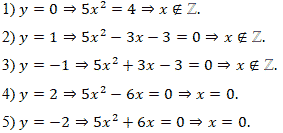
Итак, уравнение имеет ровно 2 целых решения: (0;2), (0;–2).

Ответ: (0;2), (0;–2).

Решите в целых числах 5х²+5у²+8ху+2у-2х+2=0.

Решение:

Если попытаться решить данное уравнение методом разложения на множители, то это достаточно трудоёмкая работа, поэтому это уравнение можно решить более изящным методом. Рассмотрим уравнение, как квадратное относительно х

5х²+ (8у - 2)х + 5у²+ 2у + 2 = 0

D = (8у - 2)² - 4·5(5у² + 2у + 2) = 64у² - 32у + 4 = -100у²- 40у – 40= = -36(у²+ 2у + 1) =

-36(у + 1)²

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1)²= 0. Это возможно при у = -1, тогда х = 1.

Ответ: (1;-1)

Решите уравнение 5х² - 2ху + 2у² - 2х – 2у + 1= 0.

Решение:

Рассмотрим данное уравнение как квадратное относительно х с коэффициентами, зависящими от у, 5х² - 2(у + 1)х + 2у² – 2у + 1= 0.

Найдём четверть дискриминанта D/4=(y+1)²-5(2y²-2y+1)=-(3y-2)².

Отсюда следует, что уравнение имеет решение только тогда, когда -(3у – 2)² = 0 , отсюда следует у = ⅔, затем находим х = ⅓.

Ответ: (⅓; ⅔).

Решить уравнение х ² – 6x + y – 4√y + 13 = 0.

Решение:

Решим уравнение как квадратное относительно x. Найдем дискриминант:

D = 36 – 4(y – 4√y + 13) = -4y + 16√y – 16 = -4(√y – 2) ². Уравнение будет иметь решение только при D = 0, т. е. в том случае, если y = 4.

Подставляем значение y в исходное уравнение и находим, что x = 3.

Ответ: (3; 4).