«Основные понятия комбинаторики. Решение задач на подсчёт числа размещений, перестановок, сочетаний»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА 

УЧЕБНОГО   ЗАНЯТИЯ

Тема: «Основные понятия комбинаторики. Решение задач на подсчёт числа размещений, перестановок, сочетаний»

Выполнила:

преподаватель

математики

Тимохина Л.Н.

СОДЕРЖАНИЕ

Пояснительная записка

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов, называется комбинаторикой.

Основа хорошего понимания комбинаторики умение считать, думать, рассуждать, находить удачные решения задач. Все эти навыки и способности можно выработать, если быть настойчивым, трудолюбивым и внимательным на уроках, самостоятельно и с интересом заниматься.

Учебное занятие по теме «Основные понятия комбинаторики. Решение задач на подсчёт числа размещений, перестановок, сочетаний» Задачи на подсчет числа размещений, перестановок, сочетаний, решение задач на перебор вариантов знакомит обучающихся с новым разделом математики: «Комбинаторика, статистика и теория вероятностей», основными понятиями и задачами, использованием в практических целях и в жизни человека.

Задачи с использованием элементов комбинаторики входят в состав экзамена по математике. Поэтому у обучающихся должны формироваться первоначальные представления о комбинаторных задачах.

На занятии будут использованы такие виды деятельности, как практические, самостоятельные работы, решение задач. Данный урок поможет обучающимся по-другому посмотреть на окружающий мир. После данного занятия они смогут объективно оценивать некоторые вещи, опираясь на математические подсчеты.

Они учатся решать комбинаторные задачи на «перестановки», «сочетания», «размещения» по формулам, что развивает логическое мышление.

Данная тема является первым занятием в разделе «Комбинаторика, статистика и теория вероятностей» рабочей программы.

Предварительно была подготовлена презентация по теме. Решение задач на повторение метода перебора вариантов, дерева возможных вариантов, правила произведения, которые наглядно демонстрирует основные шаги объяснения предыдущего материала. Так же были подготовлены листы с таблицами «Верите ли вы, что…», где студенты должны ответить на вопросы в начале занятия и вернуться к ним в конце занятия. Карточки с самостоятельной работой.

 Современное общество живёт в ситуации постоянных изменений ценностей и идеалов, при высокой степени неопределённости условий принятия решений и неоднозначности многих жизненных выборов. В связи с этим большое значение приобретает целенаправленная работа техникума по формированию у подрастающего поколения целостного взгляда на мир и место человека в этом мире.

Проведённый мною учебное занятие осуществляет в первую очередь задачу системности использованию полученных знаний в жизни человека. На уроке применила мультимедийный проектор, компьютер, материалы презентации, дидактический материал для индивидуальной и групповой работы на занятии.

Данная методическая разработка может быть использована учителями общеобразовательных школ, преподавателями СПО. При воплощении можно опираться на основную идею или фрагменты данной методической разработки, вносить изменения и дополнения, учитывая свой опыт.

План учебного занятия

           Учебное занятие разработано по учебной дисциплине ОУП.10   МАТЕМАТИКА для студентов 1 курса, специальности 34.02.01  Сестринское дело, медицинская сестра/медицинский брат.

Тема учебного занятия: «Основные понятия комбинаторики. Решение задач на подсчёт числа размещений, перестановок, сочетаний»

Цель: повторить основные понятия комбинаторики с помощью решения задач, используя формулы перестановки, размещения и сочетания.

Задачи:

Обучающие:

- создать условия для осознанного понимания решения простейших задач на применение элементов комбинаторики;

- повторить  формулы размещения, перестановки и сочетания;

- сформировать у студентов умения и навыки решения задач;

- продолжить формирование у студентов представления о комбинаторике и ее применении в жизни человека.

Развивающая:

- развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения;

- развивать умения сравнивать, систематизировать, обобщать.

Воспитательные:

- воспитывать чувство ответственности за качество и результат выполняемой работы;

- формировать культуру математической речи;

- воспитание дружелюбного отношения друг другу, умение работать коллективе.

Планируемые образовательные результаты:

личностные

-умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи,

-умение контролировать процесс и результат учебной математической деятельности;

-способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

метапредметные

-умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

-умение применять теоретические знания в реальных жизненных ситуациях

предметные

-        овладение навыками устных и письменных вычислений;

-        умение точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии;

-         вычислять значения выражений, выбирая удобный порядок действий.

Обучающиеся должны знать: Формулы основных соединений элементов в группы без их повторений. Основные правила расчета выражений с факториалами.

Обучающиеся должны уметь: Выполнять преобразования выражений, содержащих формулы сочетаний, размещений, перестановок без их повторений. Вычислять факториал числа, а также рассчитывать комбинации чисел с факториалами.

Развитие общих компетенций:

-              ОК 4. Осуществлять поиск и использовать информацию, необходимую для эффективного выполнения профессиональных задач, профессионального и личностного развития.

-              ОК 6.  Работать в коллективе и команде, взаимодействовать с руководством, коллегами, социальными партнерами.

            ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий

Тип учебного занятия: комбинированный.

Формы работы обучающихся: фронтальная; индивидуальная форма организации познавательной деятельности 

Необходимое техническое оборудование:

Учебно-методическое обеспечение урока:

-                  дидактические средства и методические средства: тексты самостоятельной работы; 

-                  технические средства: проектор, экран, ноутбук с презентацией, листы с опорным конспектом, задачами, учебная доска.

Учебно-материальное оснащение:

1.                  Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень). – 5-е изд. – М.: Издательский центр «Академия», 2014.

2.                 Башмаков М.И. Математика: 10 класс. Сборник задач: среднее (полное) общее образование. – 3-е изд. – М.: Издательский центр «Академия», 2017г.

Хронокарта занятия

Ход учебного занятия

I.                  Организационный момент.

II.               Мотивация учебной деятельности (постановка цели и задач занятия).

III.           Актуализация знаний

1.     Фронтальный опрос.

2.     Решение задач на повторение.

IV.            Изучение нового материала

1.                Введение понятия перестановка, формулы перестановки, решение задач.

2.                Введение понятия размещение, формулы размещения, решение задач.

3.     Введение понятия сочетание, формула сочетания, решение задач.

V.               Закрепление (решение задач).

VI.            Подведение итогов (домашнее задание, рефлексия).

VII.        Самостоятельная работа.

Ход занятия

I.                  Организационный момент. Здравствуйте, ребята! Отметка студентов отсутствующих на занятии.

II.              Мотивация учебной деятельности.

Вперед поедешь – голову сложишь,

направо поедешь – коня потеряешь, налево поедешь – меча лишишься.

- Какая проблема возникла перед богатырем? (Проблема выбора дальнейшего пути движения).

- Как богатырь выходит из данной ситуации? (А дальше говорится о том, как он выходит из данного положения, в которое попал в результате выбора).

- А вы когда-нибудь находились перед выбором? И как часто это происходит в вашей жизни?

Выбирать разные пути или варианты приходится каждому человеку. Эти пути и варианты складываются в самые разнообразные комбинации.

- Какой раздел математики занят поисками ответов на эти вопросы? (комбинаторика).

«Учимся не для техникума, а для жизни»

Сенека ЛюцийАнней

Эти слова, я хочу взять эпиграфом к нашему занятию. Так как постоянно вы задаете вопросы: «А зачем она нам нужна?», «Может ли она чем-то помочь в реальной жизни?»…

Перед вами листочек с таблицей «Верите ли вы, что…»

- Раз мы говорим о комбинаторике, сегодня мы повторим основные понятия, правила комбинаторики, и их применение при решении задач. Введем понятия перестановки, размещения и сочетания. Тема будет написана на доске.

III.           Актуализация знаний.

1. Фронтальный опрос:

- Дайте определение комбинаторики. (На каждой парте лежат листочки с опорными конспектами, ребята внимательно читают определения, один зачитывает громко всей группе, каждый повторяет еще раз и проговаривают между собой). (Комбинаторика – это раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных элементов).

- Дайте определение факториала числа. (Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число) или n –факториалом называется произведение первых подряд идущихn натуральных чисел).

- Как обозначается факториал? (Обозначается факториал восклицательным знаком-!).

- Чему равен факториал 0 и 1? (Факториал 0 и 1 равен единице).

- Сформулировать правило произведения и суммы.

Правило суммы.  Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно

n + m способами.

Правило произведения.  Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k  способами, то все k действий вместе могут быть выполнены:

2. Решение задач

1) Вычислите факториалы следующих чисел.

3! =6    5! = 120       6! = 720     7! = 50400!=1

2) Вычислите значения выражений.

а) 5!+6!  = 120+720=840

б) .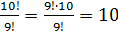

3) Упростить выражение: а) ; б) .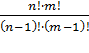

4) Решить задачу: а) Из пункта Aв B ведут три дороги, из Bв C пять дорог, из С в D четыре дороги. Сколько вариантов проезда у водителя из пункта А в В?

           ^{А             В               С              Д}

Решение: .

б) Значение цветов флага России:

белыйцвет - символизирует мир, чистоту, непорочность, совершенство;

синийцвет –символизирует веру, верность и постоянство;

красныйцвет - символизирует энергию, силу, кровь, пролитую за Отечество.

Задача: Сколько можно получить различных флагов, состоящих из 3-х горизонтальных цветных полос: красной, белой и синей? (первый ряд методом перебора, второй ряд – методом дерева возможных вариантов, третий ряд – по правилу произведения).

- Как называются задачи такого типа? (Задачи такого типа называются комбинаторными задачами).

- Вы сейчас предложили несколько способов решения выше указанной задачи. Но есть еще способ решения данной задачи – это решение с использованием основных понятий комбинаторики (перестановки, размещения, сочетания). Давайте более подробно остановимся на каждом понятии.

IV. Изучение нового материала. Перестановки, размещения, сочетания.

1. Перестановки. Перестановками из n элементов называются такие соединения из всех   n элементов, которые отличаются друг от друга порядком расположения элементов.

Число перестановок из n элементов обозначается символом Pn и вычисляется по формуле:Pn = n!

Вернемся к нашей задаче.

Задача 1.Сколько можно получить различных флагов, состоящих из 3-х горизонтальных цветных полос: красной, белой и синей?

Pn = n! = 3! = 1*2*3=6 (способов)

Ответ: 6 способов.

Задача 2.

Проказница-Мартышка,

Осёл,

Козёл

Да косолапый Мишка

Затеяли сыграть Квартет.

Достали нот, баса, альта, две скрипки

И сели на лужок под липки —

Пленять своим искусством свет.

Сколькими способами герои могли пересесть?

Решение: Pn = n! = 4! = 1*2*3*4=24 (способа).

3. Размещения. Размещениями изn элементов по k в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.  Количество размещений обозначается  и вычисляется по формуле

Задача 3. Сколько различных двузначных чисел можно составить из множества цифр , причем так, чтобы цифры числа были различны? 
Решение: Искомое число чисел.

3. Сочетания. Сочетаниями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.Количество сочетаний обозначается  и вычисляется по формуле.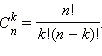

Задача 4. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Решение:

.

V. Закрепление знаний

1) Решение простейших комбинаторных задач

(Студенты работают у доски, решают простейшие комбинаторные задачи).

А) Сколькими способами можно рассадить 5 человек за столом?

Б) В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

 способами. 

В) Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

2) Найти ошибки в решениях задач:Сейчас каждый из вас выступит в роли учителя. Студент решил задачу. Проверьте, верно, ли решена задача:

А) Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

С =

Ответ: 56. (верно)

Б) Сколько четырехбуквенных слов можно образовать из букв слова сапфир?

P₄=4! = 1*2*3*4 =24 (неверно)

          (А).

VI.    Подведение итогов (домашнее задание, рефлексия).

1) Решить задачу (дифференцированные задачи)

Задача на «3»

1.                 Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.

Задачи на «4»

2.                 Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

3.                 Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?

Задача на «5»

4.                 Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

2) Рабочая тетрадь: Стр. 52-55, С/р 4.1 «Элементы комбинаторики».

Рефлексия: В качестве домашнего задания было найти ответы на вопросы: области применения комбинаторики.

учебные заведения (составление расписаний)

сфера общественного питания (составление меню)

лингвистика (рассмотрение вариантов комбинаций букв)

спортивные соревнования (расчёт количества игр между участниками)

агротехника (размещение посевов на нескольких полях)

география (раскраска карт)

биология (расшифровка кода ДНК)

криптография (разработка методов шифрования)

Я предлагаю вернуться к нашей таблице «Верите ли вы, что…» и еще раз ответить на данные вопросы.

Перед вами листочек с таблицей «Верите ли вы, что…»

- Так может ли комбинаторика помочь в реальной жизни? В чем?

VII.   Самостоятельная работа.

Вариант 1.

 1.    Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

 1) 30                          2)       100              3)       120              4) 5

 2. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

 1) 128                        2)       495                   3) 36                     4) 48

 3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

 1) 10                          2) 60                     3) 20                     4) 30

 № задания  1       2       3

 № ответа     3       2       4

Вариант 2.

 1.    Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

 1)           100              2)       30                3)       5                  4)     120

 2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

 1)           3                  2)       6                  3)       2                  4)     1

 3. Сколькими способами из 8 учебных предметов можно составить расписание учебного дня из 4 различных уроков.

 1)           10000                    2)       1680             3)       32              4)    1600

№ задания   1       2       3

№ ответа      4       1       2

Вариант 3.

 1.    Сколькими способами можно расставить 4 различные книги на книжной полке?

 1)           24                2)       4                  3)       16                4) 20

 2. Сколько диагоналей имеет выпуклый семиугольник?

 1)           30                2)       21                3)       14                4) 7

 3. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

 1)  22                         2)       11                3)       150              4)     110

№ задания   1       2       3

№ ответа      1       2       4

Вариант 4

 1.    Сколькими способами могут встать в очередь в билетную кассу 5 человек?

 1) 5        2)       120              3)       25                4)   100

 2. Сколькими способами из 15 учеников класса можно выбрать трёх  для участия в праздничном концерте?

 1) 455                           2)       45           3)       475                4)   18

 3.  В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?

 1)  600                       2)       100              3)       300              4)720

№ задания   1       2       3

№ ответа      2       1       4

Вариант 5

1.       Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?

1)             10          2) 20            3) 120                4) 50

2.                     Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?

1)             35           2) 30            3) 70                  4) 45

3.       На соревнованиях по лёгкой атлетике наш техникум представляла команда из   10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?

1)   120         2) 1560         3) 4800              4) 5040

№ задания   1       2       3

№ ответа      3          1          4

Спасибо за урок! До свидания.

Список литературы

1.     Башмаков М.И. Математика. Задачник: учебное пособие для студентов учреждений сред. проф. Образования/М.И. Башмаков. - 5-е изд., стер. -М.: Издательский центр «Академия», 2018.

2.      Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебное пособие для студентов учреждений сред. проф. Образования/М.И. Башмаков -М.: Издательский центр «Академия», 2016.

3.     Мордкович А.Г. Математика: алгебра и начала математического анализа, геометрия. 10-11 классы. В 2ч./А.Г. Мордкович, П.В. Семенов. - М.: Мнемозина, 2017г.

4.     Богомолов Н.В. Практические занятия по высшей математике. – М.: Высшая школа, 1999.

Приложения

Тесты с решением

Эталоны ответов