Основные свойства любой модели

Основные свойства любой модели

1º. Конечность. Модель отражает оригинал лишь в конечном числе его отношений.

2º. Упрощенность. Модель отражает только существенные стороны объекта, и кроме того модель должна быть проста для исследования или воспроизведения.

3º. Приблизительность. Действительность отображается моделью грубо или приблизительно.

4º. Адекватность. Модель должна успешно описывать моделируемую систему.

5º. Наглядность, обозримость основных свойств и отношений.

6º. Доступность и технологичность для исследования и воспроизведения.

7º. Информативность. Модель должна содержать достаточную информацию о системе и давать возможность получить новую информацию.

8º. Сохранение информации содержащейся в оригинале.

9º. Полнота. В модели должны быть учтены все основные связи и отношения необходимые для обеспечения цели моделирования.

10º. Устойчивость. Модель должна описывать и обеспечивать устойчивость поведения системы, даже если она в начале является не устойчивой.

11º. Замкнутость. Модель учитывает и отображает замкнутую систему необходимых основных гипотез, связей и отношений.

Компьютерное моделирование

Компьютерное моделирование – основа представления знаний в ЭВМ.

Компьютерное моделирование для рождения новой информации использует любую информацию, которую можно актуализировать с помощью ЭВМ.

Процесс моделирования связан с разработкой систем компьютерного моделирования.

Разновидностью компьютерного моделирования является вычислительный эксперимент, т. е. эксперимент осуществляемый с помощью компьютерной среды или технологии.

Вычислительный эксперимент становится новым инструментом, методом научного познания новой технологии из-за необходимости исследования сложных и нелинейных математических моделей системы.

Вычислительный эксперимент позволяет находить новые закономерности, проверять гипотезы, визуализировать ход событий.

Пример: Модель повторяющейся эпидемии.

Моделирование физической и биологической задачи

Задача 1. Задача о пушке из которой надо попасть в крепость (физическая задача).

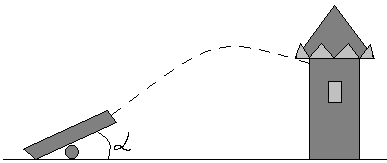
Горизонтальное x и вертикальное y – смешение снаряда за время t описывается формулами:

x = (Ư cosα) · t

y = (Ư sinα) · t – (g t² / 2)

где, g – ускорение свободного падения, t – время, α – угол наклона пушки.

Изменим математическую модель, выразим из первой формулы время t и подставим ее во вторую формулу: h = S tgα – (g S² / 2 Ư² cos²α)

Требуется найти такое значение угла α, чтобы снаряд пролетев заданное расстояние S попал на нужную высоту h.

Объяснение: Задача сводится к решению уравнения методом половинного деления, где α берется от 0 до π/4.

Метод половинного деления имеет аналог в артиллерийском приеме (пристрел) – одно положение выше цели другое ниже цели.

Задача 2. Задача о лисах и кроликах (биологическая задача).

 На некотором острове живут лисы и кролики. Кролики питаются травой, а лисы охотятся на кроликов. Экологи пересчитывая кроликов и лис установили:

1)    коэффициент прироста числа кроликов зависит от колебания погоды (холодная или теплая зима и т. д.) и колеблется в пределах от 3,2 до 4,7;

2)    коэффициент прироста числа лис при избытки крольчатины колеблется от 5,2 до 5,7. При недостатки он пропорционален приросту кроликов.

Коэффициент пропорциональности ≈ 1/C, где C – масса крольчатины в среднем съедаемая одной лисой за год (примем за 50).

Требуется установить как меняется численность кроликов и лис с течением времени

Построение модели:

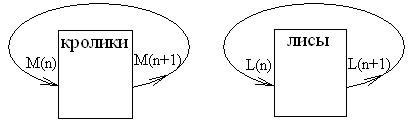
M(n) – масса кроликов через n лет.

L(n) – масса лис через n лет.

Взаимодействие лис и кроликов:

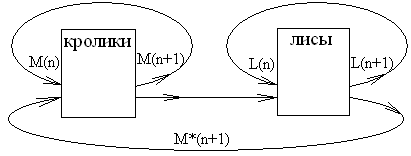
В этой динамической системе усматривается три контура обратной связи. Опишем их расчетными формулами.

Кролики: прирост иде6т в соответствии с моделью неограниченного роста. Их поедают лисы, поэтому изменение кроликов можно записать так:

M(n+1) – M(n) = k · M(n) – C · L(n)

M(n+1) = (1+k) · M(n) – C · L(n)

Лисы: если кроликов очень много, то численность кроликов растет по модели ограниченного роста, а численность лис тоже растет по модели неограниченного роста. Если крольчатины мало, то прирост определяется величиной,  показывающей сколько новых лис может прокормиться за счет прироста кроликов.

Для лис можно вывести формулу:

L(n+1) – L(n) = min (a, ) · L(n)

L(n+1) = (1 + min (a, )) · L(n)

где a- коэффициент неограниченного роста кроликов.

Заполнить электронную таблицу следующими данными:

a = 0.1

k = 4

C = 50

M(0) = 10000

L(0) = 100

Узнать, сколько кроликов и лис будет через 5 лет, 10 лет. Построить графики L(n) и M(n) как функция от n.

Основные этапы математического и инфологического моделирования

1. Постановка задачи.

    1.1. Формулировка.

    1.2. Определение цели моделирования и их приоритетов.

    1.3. Сбор информации о системе, объекте моделирования.

    1.4. Описание данных (их структуры, диапазон источника и т. д.).

2. Предмодельный анализ.

    2.1. Анализ существующих аналогов и подсистем.

    2.2. Анализ технических средств моделирования (ЭВМ и др.).

    2.3. Анализ программного обеспечения (языки программирования, инструментальные среды, пакеты программ)

   2.4.  Анализ математического обеспечения (модели, методы, алгоритмы).

3. Анализ задачи (модели).

   3.1.  Разработка структур данных.

   3.2. Разработка  входных и выходных спецификаций, форм и представлений данных.

   3.3. Проектирование структуры и состава модели (подмодели).

4. Исследование модели.

   4.1. Выбор методов исследования подмодели.

   4.2. Выбор, адаптация или разработка алгоритма.

   4.3. Сборка модели в целом из подмоделей.

   4.4. Идентификация модели если в этом есть необходимость.

   4.5. Формулировка используемых критериев адекватности моделируемой системы устойчивости и чувствительности.

5. Программирование (проектирование программы).

   5.1. Выбор метода тестирования и теста (контрольные примеры).

   5.2. Кодирование на языке программирования.

   5.3 Комментирование программы.

6. Тестирование и отладка.   

   6.1. Синтаксическая отладка.

   6.2. Семантическая отладка (отладка логической структуры).

   6.3 Тестовые расчёты, анализ результатов тестирования.

   6.4. Оптимизация программы.

7. Оценка моделирования.

   7.1. Оценка средств моделирования.

   7.2. Оценка адекватности моделируемой системы.

   7.3. Оценка чувствительности модели.

   7.4. оценка устойчивости модели.

8. Документирование.

   8.1. Описание задач и цели.

   8.2. Описание метода, алгоритма.

   8.3 Описание среды реализации.

   8.4. Описание возможностей и ограничений.

   8.5. Описаний входных и выходных форматов, спецификаций.

   8.6. Описание тестирования.  

   8.7.Описание инструкции пользователя.

9. Сопровождение.

   9.1. Анализ использования, периодичность использования возможность количества пользователей, анализ отказов.

   9.2. Обслуживание модели алгоритма программы и их эксплуатация.

   9.3.  Расширение возможностей: включение новых функций или изменение режимов моделирования.

   9.4. Нахождение , исправление скрытых ошибок в программе, если они найдутся.

10. Использование модели.