Закон всемирного тяготения

Закон всемирного тяготения

Все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Исаак Ньютон (1643–1727 )                                               

где т₁ и т₂ – массы тел; r – расстояние между телами; G – гравитационная постоянная

Открытию закона всемирного тяготения во многом способствовали законы движения планет, сформулированные Кеплером, и другие достижения астрономии XVII в.

Знание расстояния до Луны позволило Исааку Ньютону доказать тождественность силы, удерживающей Луну при ее движении вокруг Земли, и силы, вызывающей падение тел на Землю.

Так как сила тяжести меняется обратно пропорционально квадрату расстояния, как это следует из закона всемирного тяготения, то Луна,

находящаяся от Земли на расстоянии примерно 60 ее радиусов, должна испытывать ускорение в 3600 раз меньшее,

чем ускорение силы тяжести на поверхности Земли, равное 9,8 м/с .

Следовательно, ускорение Луны должно составлять 0,0027 м/с².

Исаак Ньютон (1643–1727 )

В то же время Луна, как любое тело, равномерно движущееся по окружности, имеет ускорение

где ω– ее угловая скорость, r– радиус ее орбиты.

Если считать, что радиус Земли равен 6400 км, то радиус лунной орбиты будет составлять

r= 60 • 6 400 000 м = 3,84 • 10 м. Звездный период обращения Луны Т= 27,32 суток, в секундах составляет 2,36 • 10 с.

Тогда ускорение орбитального движения Луны

Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с действующей на поверхности Земли.

При движении планет, в соответствии с третьим законом Кеплера, их ускорение и действующая на них сила притяжения Солнца обратно

пропорциональны квадрату расстояния, как это следует из закона всемирного тяготения.

Действительно, согласно третьему закону Кеплера отношение кубов больших полуосей орбит dи квадратов периодов обращения Т есть величина постоянная:

Исаак Ньютон (1643–1727 )

Ускорение планеты равно

Из третьего закона Кеплера следует

поэтому ускорение планеты равно

Итак, сила взаимодействия планет и Солнца удовлетворяет закону всемирного тяготения.

Возмущения в движениях тел Солнечной системы

Движение планет Солнечной системы не в точности подчиняется законам

Кеплера из-за их взаимодействия не только с Солнцем, но и между собой.

Отклонения тел от движения по эллипсам называют возмущениями.

Возмущения  невелики, так как масса Солнца гораздо больше массы не только отдельной планеты, но и всех планет в целом.

Особенно заметны отклонения астероидов и комет при их прохождении вблизи Юпитера, масса которого в 300 раз превышает массу Земли.

В XIX в. расчёт возмущений позволил открыть планету Нептун.

Вильям Гершель в 1781 г. открыл планету Уран.

Даже при учете возмущений со стороны всех известных планет наблюдаемое движение Урана не согласовывалось с расчетным.

На основе предположения о наличии еще одной «заурановой» планеты Джон Адамс в Англии и Урбен Леверье во Франции независимо друг от друга сделали вычисления ее орбиты и положения на небе.

На основе расчетов Леверье немецкий астроном Иоганн Галле 23 сентября 1846 г. обнаружил в созвездии Водолея неизвестную ранее планету – Нептун.

По возмущениям Урана и Нептуна была предсказана, а в 1930 году и обнаружена карликовая планета Плутон.

Открытие Нептуна стало триумфом гелиоцентрической системы,

важнейшим подтверждением справедливости закона всемирного тяготения.

Масса и плотность Земли

Закон всемирного тяготения позволил определить массу Земли.

В соответствии с законом всемирного тяготения ускорение свободного падения: , где

Зная массу и объем земного шара, можно вычислить его среднюю плотность:

.

С глубиной за счет увеличения давления и содержания тяжелых элементов плотность возрастает

Определение массы небесных тел

Более точная формула третьего закона Кеплера, которая была получена Ньютоном, дает возможность определить массу небесного тела.

Пусть два взаимно притягивающихся тела обращаются по круговой орбите с периодом вокруг общего центра масс. Расстояние между их центрами .

На основании закона всемирного тяготения ускорение каждого из этих тел равно:

 .

Угловая скорость обращения вокруг центра масс:

.

Центростремительные ускорения тел:

.

Приравняв полученные для ускорений выражения, выразив из них  и  и сложив их почленно, получаем:

откуда            .

В правой части выражения находятся только постоянные величины, поэтому оно справедливо для любой системы двух тел, взаимодействующих по закону тяготения и обращающихся вокруг общего центра масс, – Солнце и планета, планета и спутник.

Определим массу Солнца из выражения:

 ,

где М – масса Солнца; 𝑚₁ и 𝑚₂ – массы Земли и Луны; 𝑇₁ и 𝑎₁ – период обращения Земли вокруг Солнца (год) и

большая полуось ее орбиты; 𝑇 и 𝑎₂ – период

Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они оказывают на движение астероидов, комет или космических аппаратов, пролетающих в их окрестностях.

Приливы

Под действием взаимного притяжения частиц тело стремится принять форму шара. Если эти тела вращаются, то они деформируются, сжимаются вдоль оси вращения.

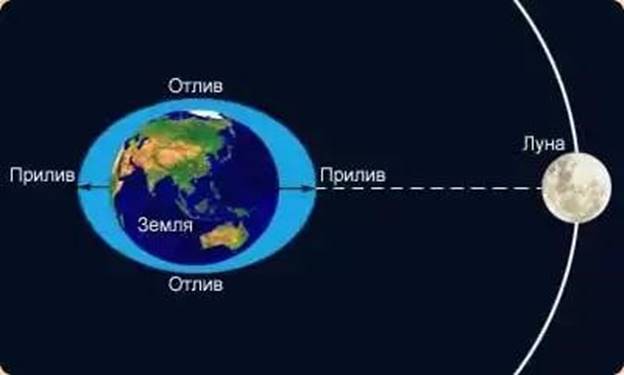
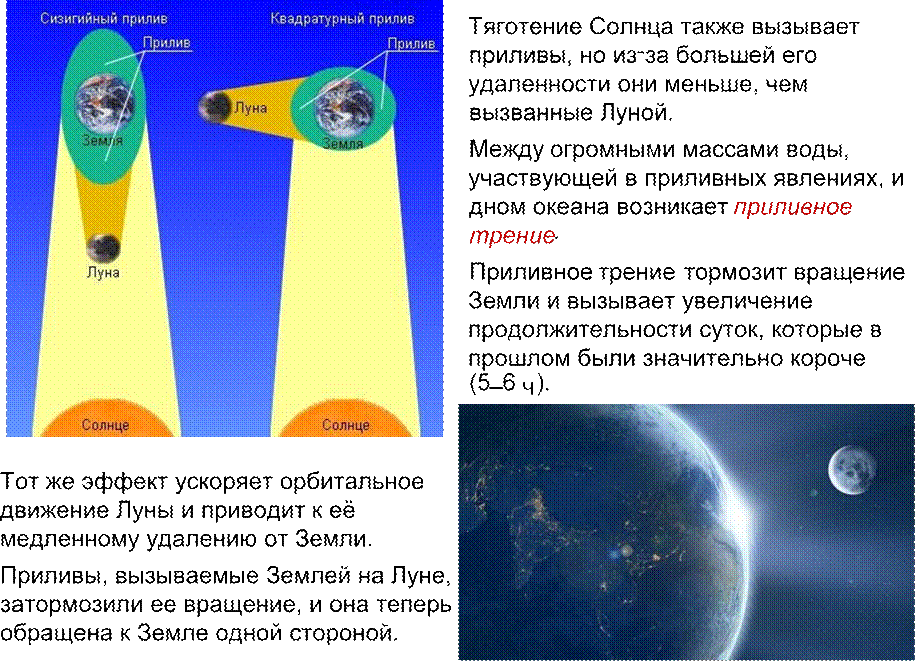
Кроме того, изменение их формы происходит и под действием взаимного притяжения, которое вызывают явления, называемые приливами.

Вопросы (с.80)

1.       Почему движение планет происходит не в точности по законам Кеплера?

2.       Как было установлено местоположение планеты Нептун?

3.       Какая из планет вызывает наибольшие возмущения в движении других тел Солнечной системы и почему?

4.       Какие тела Солнечной системы испытывают наибольшие возмущения и почему?

Домашнее задание

1)   § 14 (п.1-5).

2)   Упражнение 12 (с.80)

1. Определите массу Юпитера, зная, что его спутник, который отстоит от Юпитера на 422 000 км, имеет период обращения 1,77 суток.

Для сравнения используйте данные для системы Земля–Луна.