Открытый урок по математике в 9 классе по теме: « Всюду геометрия!»

 

Открытый урок по математике в 9 классе

по теме: « Всюду геометрия!»

Тема: «Все вокруг геометрия!».

Класс: 9

Цель: повторить и систематизировать знания по теме «Площадь многоугольников».

Задачи:

образовательные:

1.формировать навыки самостоятельного воспроизведения ранее полученных знаний;

2.формировать навыки использования полученных знаний по теме площадь многоугольников в жизненных ситуациях;

3.готовиться к сдаче ГИА.

развивающие:

1.развитие мышления обучающихся, развитие математической речи;

2.развитие коммуникативных умений  и интеллектуальных способностей посредством взаимодействия в процессе выполнения заданий;

воспитательные: 

1. воспитание способностей к нравственному общению среди обучающихся, к сотрудничеству, то есть формирование коммуникативных навыков.;

2. воспитание ответственности, организованности.

Тип урока: комплексного применения знаний (комбинированный), обобщения и систематизации знании.

Оборудование: учебник Л.С. Атанасяна Геометрия 7-9, проектор, компьютер, листы с изображением многоугольников, задания для индивидуальной работы.

Методы: проблемно-поисковой метод

Формы познавательной деятельности учащихся: групповая, индивидуальная, коллективная.

Структура урока:

1.                  Организационный момент;

2.                  Актуализация опорных знаний и их коррекция;

3.                  Мозговой штурм;

4.                  Информация о домашнем задании;

5.                  Рефлексия.

План урока:

1.                  Организационный момент.

-Подумайте и ответьте на вопрос: зачем нужно изучать геометрию?

«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» Галилео Галилей

Великий французский архитектор Корбюзье  в начале 20 века как-то воскликнул: «Все вокруг геометрия!».

-Как вы понимаете эту фразу? Согласны ли вы с ним? Сегодня уже в начале 21-го столетия мы можем повторить это восклицание с еще большим изумлением. В самом деле, посмотрите вокруг — всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики.  Из ваших слов я поняла, воистину, современная цивилизация — это Цивилизация Геометрии.

-Для каких современных специальностей нужны человеку геометрические знания, умения? Используем ли мы геометрические знания в быту?

Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых. Невозможно выполнить ремонт квартиры не владея элементарными знаниями по геометрии.

2. Мотивация выбора данной темы:

Цель: сформулировать тему и цели урока.

 И я вам сегодня предлагаю решить задачу практического содержания:

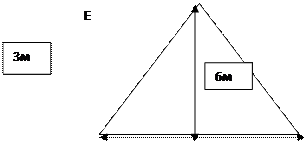
Чтобы построить дом садоводу надо докупить землю у соседа. За каждый квадратный метр сосед просит 5 тысяч рублей. Выберите самый дешевый вариант проданного земельного участка, если первоначальные формы домов представлены на рисунке:

 

 

10 м

А

 

 

 

 

 

 

 

 

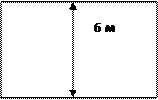
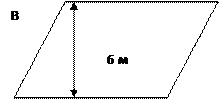
F

D

							6м
	6м
						6 м

 

 

 

 

 

 

-Что необходимо знать, чтобы сделать правильный выбор?( Площади данных фигур)

- Сформулируйте тему сегодняшнего урока. Каковы его цели? (тему и цели повесить на доску, чтобы они были видны учащимся на протяжении всего урока.

Итак , цели: 1)Повторить формулы для нахождения площадей  многоугольников.

                      2)Учиться применять формулы при решении задач с практическим содержанием.

3. Актуализация опорных знаний и их коррекция.

Цель: восстановить в памяти знания, необходимые для решения задач.

-Как можно классифицировать фигуры, на слайде?( Треугольники, четырёхугольники) (Правильные , неправильные многоугольники)

-Работа в парах. Заполните таблицу, впишите формулы, соответствующие данным фигурам)

1) S = ab  2) S = ah_a  3) S = ab  4) S = d₁d₂   5) S = a²   6) S = (a + b) h   7) S = ab sin α

8) S =  d²   9) S =    10) S =  d₁d₂ sin α    11) S=ПR²  12) S=

13) S=pr, г - радиус вписанной окружности 

14) S=,  R- радиус описанной окружности

15) S=     16) S = ab sin α   17) S=  ah_a   18) S=  ch_c   19) S = a² sin α

20) S =  d₁d₂  

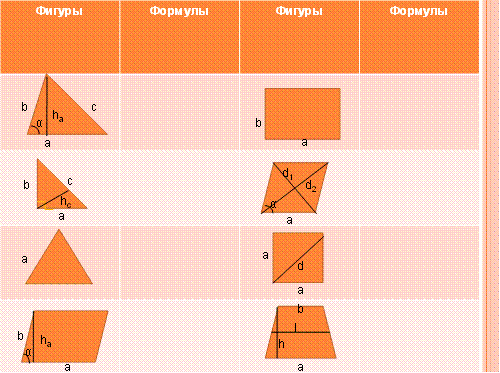
Проверьте, все ли формулы вы смогли выписать. Обсудим полученные результаты.

4.Отработка практических навыков. Работа в группах по 4 человека.

Цель: отработать применение формул на практике.

Решить задачу практического содержания, рассмотренную в начале урока.

Стоимость  дома А 10*6*5000=300000 рублей

Стои мость дома В 6*10*5000=300000 рублей

Стоимость дома С (12*6-1,5*2*4)*5000=240000 рублей

Стоимость дома Е ½*6*10*5000=150000 рублей

Стоимость дома D ½* 6*6*5000=90000рублей

Стоимость дома F ½*(6+10)*6*5000=240000 рублей

Самая дешевая земля под постройку дома в форме прямоугольного треугольника.(D=18 )

 5. Самостоятельная работа с самопроверкой (по вариантам).

 Решение задач из 1 части ГИА.

Цель: выявить пробелы в знаниях и провести корректировку.

1 вариант

1)Токарь выточил деталь в форме прямоугольного треугольника. Один из его катетов равен 10 см, а острый угол, прилежащий к нему 30⁰ . Найдите площадь полученной детали.

2)Сколько понадобится плиток в форме равнобедренного треугольника, периметр которого равен 16 см, а основание- 6 см, чтобы облицевать ими стену прямоугольной формы со сторонами 8 м и 3 м?

2вариант

1)Около дома разбили клумбу в форме ромба, периметр которого равен 8 м , а один из углов равен 30⁰ . Найдите площадь клумбы.

2)Сколько понадобится дощечек паркета в форме прямоугольного треугольника с гипотенузой 10 см и одним из острых углов 45⁰ , чтобы выложить ими квадратный пол со стороной 5 м?

При затруднении решения задачи можно воспользоваться подсказкой ( Перевёрнутые листы на доске с номером варианта и задания. На них дана формула, которой нужно воспользоваться или план решения задачи) . Подсказки (Приложение1)

Проверка результатов. Разбор задач с теми, у кого не получилось.

У кого нет вопросов дополнительная задача. (за верное выполнение ставится отметка)

 (дополнительная задача)

 

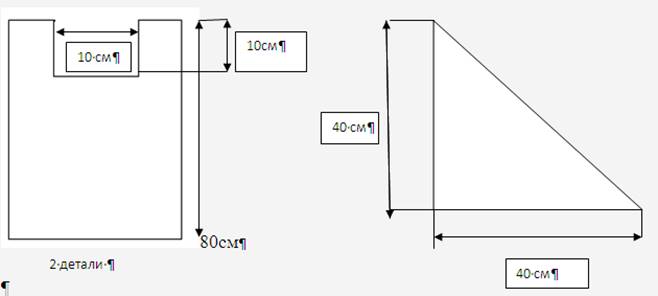
Для маленькой Анны в ателье по пошиву одежды на лето мама заказала сшить платье и косынку из ткани одного цвета. План раскройки ткани изображен на рисунке.

 

30 см

Какую сумму надо заплатить за пошив платья, если

 

Стоимость ткани за 1кв. м	300 рублей
Раскройка ткани Платье детское Косынка	45 рублей 15 рублей
Пошив платья Пошив косынки	150 рублей 50 рублей
Обметывание косынки цветными нитками с 2 сторон за 1 кв.м Обметывание платья за 1 кв. метр	35 рублей 15 рублей

 

S = 2*80*30=4800 кв.см = 0,48 кв.м

S горловины = 2*10*10= 200 кв.см= 0,02 кв.м

S платья = 0,48-0,02=0,46 кв.м

S косынки = ½*40*40= 800 кв.см=0,08 кв.м

S общая площадь ткани = 0,46+ 0,08=0,54 кв.м

Стоимость ткани 0,54*300=162 рубля

Стоимость раскроя и пошива 45+15+150+50=260 рублей

Стоимость обметки платья 2*(80*2+2*10+30*2)=480см = 4,8м

4,8*15=72 рублей

Стоимость косынки 40+40=80см=0,8м

35*0,8=28 рублей

Общая сумма платья и косынки 162+260+72+28= 522 рубля

Спасибо очень хорошо поработали.

 

Рефлексия. Ответьте на вопросы:

¢  Пригодятся ли на практике мне эти знания?

¢  Где я смогу применить эти знания?

Притча: Шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил тяжелые камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»

-          Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.

-          Кто возил камни? Кто выполнял свою работу?  Кто строил храм?

 

Дом. задание: 1)задача про пошив платья, 

                           2)составьте свои задачи с практическим содержание на использование формул площади многоугольников, запишите их условие и решение.

 Приложение 1

Подсказки:

№1(1 вариант)

1)Из прямоугольного  ΔАВС можно найти:

 1 способ:  АВ, если cos=  и cos=

2 способ: ВС, если tg=  и tg=

3 способ:  ВС=х, АВ=2х(т.к. гипотенуза в 2 раза больше катета, лежащего напротив угла в . Далее составить квадратное уравнение, используя теорему Пифагора =+и найти х=ВС.

2) Использовать формулу для нахождения площади треугольника.

№1(2 вариант)

1)Найти сторону ромба АВ, если АВ=ВС=СD=DА и Р=8м.

2)Найти площадь ромба, используя формулу площади параллелограмма( т.к. ромб- параллелограмм) sin=  

№2(1 вариант)

1)Найти боковые стороны ΔАВС, если АВ=АС и

 АВ+АС+ВС=16 см.

2) Вычислить площадь  ΔАВС:

1 способ: По формуле Герона.

2 способ: Из ΔАВН найти высоту АН по теореме Пифагора АН=.И использовать формулу для нахождения площади треугольника.

3)Вычислить площадь прямоугольника.

4)Кол-во плиток=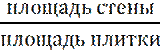

1=10000

№2(2вариант)

1)     Вычислить площадь ΔАВС

1 способ:Найти АС: cos=  и cos=  .Далее формулу

 S =  ab sin α,   sin=  .

2 способ: Найти ВС=АС=х, используя теорему Пифагора =+. Далее формулу  S =  ab

         Вычислить площадь квадрата.

 

2)       Кол-во дощечек=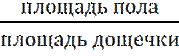   

1=10000

Методическая литература, интернет ресурсы:

1)     http://karmanform.ucoz.ru

2)     http://mathgia.ru

3)     Сергеев И.Н., Олехник С.Н., Гашков С.Б. “Примени математику”, М., Наука, 1989.

4)     Смирнова И.М., Смирнов В.А. «Геометрические задачи с практическим содержанием», 2010

5)     Балк М.Б., Балк Г.Д. “Математика после уроков”, М., Просвещение, 1971.

 

Скачано с www.znanio.ru