"Параллельные прямые". Контрольная работа. Геометрия 7 класс. УМК А.А. Берсенев, Н.В. Сафонова.

Контрольная работа №3 по теме «Параллельные прямые».

Вариант №1.

1.     Выбрать верные утверждения:

1) Две прямые на плоскости называются параллельными, если они не пересекаются на данном чертеже.

2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

3) Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

4) Если две параллельные прямые пересечены секущей, то вертикальные углы равны.

5) Если прямая, перпендикулярна одной из параллельных прямых, то другую прямую она не пересекает.

6) При пересечении двух прямых секущей образуются вертикальные и смежные углы.

7) Аксиома – это утверждение, требующее обоснований.

2.     Найти все углы, образовавшиеся при пересечении двух параллельных прямых а и в секущей с, если один из углов равен 67⁰.

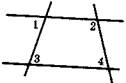
3.     На рисунке 1 = 82⁰, 2 = 119⁰, 3 = 82⁰. Найти 4.

4.  Отрезок АD – биссектриса треугольника АВС. Через точку D проведена    прямая, параллельная стороне АВ и пересекающая сторону АС в точке К. Вычислить градусные меры углов треугольника АDК, если                   ВАС = 64⁰.

Вариант №2.

1.     Выбрать верные утверждения:

1) Две прямые на плоскости называются параллельными, если они находятся на равном расстоянии друг от друга.

2) Если при пересечении двух прямых секущей сумма соответственных углов равна 180⁰, то прямые параллельны.

3) Через точку, не лежащую на плоскости проходит только одна прямая, параллельная данной.

4) Если две параллельные прямые пересечены секущей, то сумма накрест лежащих углов рана 180⁰.

5) Если прямая, перпендикулярна одной из параллельных прямых, то другой она параллельна.

6) При пересечении двух прямых секущей образуются острые, прямые и тупые углы.

7) Аксиома – это утверждение, не требующее обоснований.

2.     Найти все углы, образовавшиеся при пересечении двух параллельных прямых а и в секущей с, если один из углов равен 114⁰.

3. 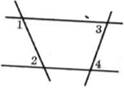    На рисунке 1 = 112⁰, 2 = 68⁰, 3 = 63⁰. Найти 4.

4. Отрезок МТ – биссектриса треугольника МРК. Через точку Т проведена    прямая, параллельная стороне МР и пересекающая сторону МК в точке Е. Вычислить градусные меры углов треугольника МТЕ, если                   ТЕМ = 130⁰.

Вариант №3.

1.     Выбрать верные утверждения:

1) Две прямые на плоскости называются параллельными, если они перпендикулярны одной прямой.

2) Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны.

3) Если прямые параллельны третьей прямой, то они параллельны.

4) Если две параллельные прямые пересечены секущей, то соответственные углы равны.

5) Если прямая, перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

6) При пересечении двух прямых секущей образуются параллельные и перпендикулярные углы.

7) Аксиома – это утверждение, имеющее следствие.

2.     Найти все углы, образовавшиеся при пересечении двух параллельных прямых а и в секущей с, если один из углов равен 77⁰.

3. 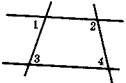    На рисунке 1 = 69⁰, 2 = 132⁰, 3 = 69⁰. Найти 4.

4.     Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена    прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Вычислить градусные меры углов треугольника DМN, если СDЕ = 56⁰.

Вариант №4

1.     Выбрать верные утверждения:

1) Две прямые на плоскости называются параллельными, если они не пересекаются.

2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

4) Если две параллельные прямые пересечены секущей, то односторонние углы равны.

5) Если прямая, перпендикулярна одной из параллельных прямых, с другой прямой она совпадает.

6) При пересечении двух прямых секущей образуются накрест лежащие, соответственные и односторонние углы.

7) Аксиома – это утверждение, обратное к которому верно.

2.     Найти все углы, образовавшиеся при пересечении двух параллельных прямых а и в секущей с, если один из углов равен 123⁰.

3.     На рисунке 1 = 109⁰, 2 = 71⁰, 3 = 74⁰. Найти 4.

4.     Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Вычислить градусные меры углов треугольника АDF, если ВАС = 72⁰.