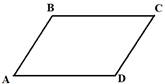
Параллелограмм(основные свойства)

Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны. К тому же стоит отметить, что параллелограмм-это выпуклый четырёхугольник, поскольку его диагонали пересекаются.

Перечислим свойства, которыми обладает данный четырёхугольник:

1.      Противоположные стороны равны

2.     Противоположные углы равны

3.      Диагонали пересекаются и точкой пересечения делятся пополам

4.     Сумма квадратов всех сторон равна сумме квадратов диагоналей.

А теперь обратимся к признакам данной фигуры. Четырёхугольник является параллелограммом, если выполняется любое из следующих условий:

1.     Противоположные стороны четырёхугольника попарно равны

2.     Противоположные углы четырёхугольника попарно равны

3.     Диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам

4.     Две стороны четырёхугольника равны и параллельны

Формулы для вычисления площади параллелограмма

I способ

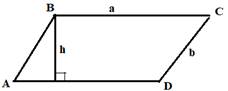
Площадь параллелограмма равна произведению его высоты на сторону, на которую она опущена.

II способ

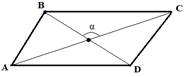
Площадь параллелограмма равная полупроизведению диагоналей на синус угла между ними.

Среди теории, связанной с параллелограммом, следует указать теорему Фалеса, которой не уделяется должного внимания в учебнике, но она может сильно помочь при решении многих задач.

Итак, теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую

Помимо теоремы Фалеса следует рассмотреть ещё одну теорему-теорему Вариньона: Середины сторон произвольного четырёхугольника являются вершинами параллелограмма.