Перевод чисел из одной системы счисления в другую. Представление информации, языки, кодирование. Измерение информации. Объемный подход. Содержательный подход.

Лекция №2

ТЕМА: Перевод чисел из одной системы счисления в другую. Представление информации, языки, кодирование. Измерение информации. Объемный подход. Содержательный подход.

 

ЦЕЛЬ:    Закрепить алгоритмы перевода чисел из одной системы счисления в другую. Рассказать о различных способах представления информации,  целях и способах кодирования и декодирования информации. Познакомиться с историей технических способов кодирования информации. Научиться, как измерять объем информации (объемный подход). Рассмотреть понятие «содержательного подхода» в информатике.  Развивать интерес к предмету, способствовать воспитанию и формированию информационной культуры.

 

План лекции:

1. Повторение пройденного материала.

2. Закрепление полученных навыков перевода чисел из одной СС в другую.

3. Тест по теме: «Информация. Информационные процессы. Перевод чисел из одной системы счисления в другую».

4. Представление информации, языки, кодирование. Измерение информации. Объемный подход. Содержательный подход.

5. Домашнее задание.

 

Ход занятия:

1. Повторение пройденного материала.

1) Наука информатика.

2) В чем состоит функция и задачи информатики?

3) Что такое информация? Свойства информации.

4) Какие способы и формы передачи информации вам известны?

5) Что такое информационные процессы, технологии?

6) Что такое шум?

7) В каких видах может быть представлена информация?

8) Единицы измерения информации

9) Что такое система счисления?

10) Какие виды СС вам известны?

 

2. Закрепление полученных навыков перевода чисел из одной СС в другую.

Перевести в двоичную СС: 216, 336, 530, 384.

Перевести в десятичную СС: 1100000110, 1100010, 10100011, 110001001.

3. ТЕСТ ПО ТЕМЕ:

«ИНФОРМАЦИЯ. ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ »

1. Информацию, изложенную на доступном для получателя языке называют:

a)       полной;

b)       полезной;

c)       актуальной;

d)       достоверной;

e)       понятной.

2. Информацию, не зависящую от личного мнения или суждения, называют:

a)       достоверной;

b)       актуальной;

c)       объективной;

d)       полной;

e)       понятной.

3. Информацию, отражающую истинное положение вещей, называют:

a)       полной;

b)       полезной;

c)       актуальной;

d)       достоверной;

e)       понятной.

4. Информацию, существенную и важную в настоящий момент, называют:

a)       полной;

b)       полезной;

c)       актуальной;

d)       достоверной;

e)       понятной.

5. Наибольший объем информации человек получает при помощи:

a)       органов слуха;

b)       органов зрения;

c)       органов осязания;

d)       органов обоняния;

e)       вкусовых рецепторов.

6. Тактильную информацию человек получает посредством:

a)       специальных приборов;

b)       термометра;

c)       барометра;

d)       органов осязания;

e)       органов слуха.

7. Сигнал называют аналоговым, если

a)       он может принимать конечное число конкретных значений;

b)       он непрерывно изменяется по амплитуде во времени;

c)       он несет текстовую информацию;

d)       он несет какую-либо информацию;

e)       это цифровой сигнал.

8. Сигнал называют дискретным, если

a)       он может принимать конечное число конкретных значений;

b)       он непрерывно изменяется по амплитуде во времени;

c)       он несет текстовую информацию;

d)       он несет какую-либо информацию;

e)       это цифровой сигнал.

9. Во внутренней памяти компьютера представление информации

a)       непрерывно;

b)       дискретно;

c)       частично дискретно, частично непрерывно;

d)       информация представлена в виде символов и графиков.

10. Аналоговым сигналом является:

a)       сигнал светофора;

b)       сигнал SOS;

c)       сигнал маяка;

d)       электрокардиограмма;

e)       дорожный знак.

11. Дискретный сигнал формирует:

a)       барометр;

b)       термометр;

c)       спидометр;

d)       светофор.

12. Измерение температуры представляет собой:

a)       процесс хранения информации;

b)       процесс передачи информации;

c)       процесс получения информации;

d)       процесс защиты информации;

e)       процесс использования информации.

13. Перевод текста с английского языка на русский можно назвать:

a)       процесс хранения информации;

b)       процесс передачи информации;

c)       процесс получения информации;

d)       процесс защиты информации;

e)       процесс обработки информации.

14. Обмен информацией - это:

a)       выполнение домашней работы;

b)       просмотр телепрограммы;

c)       наблюдение за поведением рыб в аквариуме;

d)       разговор по телефону.

 

15. Двоичное число 10001₂ соответствует десятичному числу

a)       11₁₀

b)       17₁₀

c)       256₁₀

d)       1001₁₀

e)       10001₁₀

16. За единицу количества информации принимается:

a)       байт

b)       бит

c)       бод

d)       байтов

17. В какой из последовательностей единицы измерения указаны в порядке возрастания

a)       гигабайт, килобайт, мегабайт, байт

b)       гигабайт, мегабайт, килобайт, байт

c)       мегабайт, килобайт, байт, гигабайт

d)       байт, килобайт, мегабайт, гигабайт

18. Какое количество цифр используется в десятичной системе  счисления?

a)       8

b)       11

c)       10

d)       2

19. Переведите число 101010101 из двоичной системы счисления в десятичную

a)       361

b)       564

c)       455

d)       341

20. Сколько байтов в 4 Кбайтах?

a)       4 * 10⁶

b)       4 * 2¹⁰

c)       4 * 10²¹

d)       4 * 2³²

21. Каков результат перевода числа 216 из десятичной системы счисления в двоичную?

a)       11001100

b)       11011000

c)       11100000

d)       11001000

22. Число 32 в десятичной системе эквивалентно числу в двоичной системе...

a)       100000

b)       35

c)       21

d)       1000

23. Сколько цифр в двоичной системе счисления

a)       1

b)       0

c)       2

d)       3

24. Не является свойством информации

a)       Понятность

b)       Полнота

c)       Прямолинейность

d)       Доступность

25. Килобайт - это...

a)       1000 символов

b)       8 бит

c)       1000 байт

d)       1024 байт

26. Одним из основных свойств информации является

a)       Доступность

b)       Результативность

c)       Хаотичность

d)       Измеримость

27. Какое из приведенных ниже равенств верно?

a)       5₁₀ = 00000111₂

b)       47₁₀ = 101111₂

c)       13₁₀ = 00011111₂

d)       2₁₀ = 00001000₂

28. Не является носителем информации...

a)       Книга

b)       Глобус

c)       Ручка

d)       Видеопленка

29. Считая, что каждый символ кодируется одним байтом, оцените информационный объем фразы: "Один пуд - около 16,4 килограмма"

a)       32 Кбайта

b)       512 бит

c)       64 бита

d)       32 байта

30. Сколько байт информации содержит сообщение объемом 216 бит

a)       16

b)       28

c)       27

d)       32

31. Сообщение, информационный объем которого равен 32  битам, соответствует объему информации в байтах...

a)       5

b)       2

c)       3

d)       4

 

32. Сообщение, имеющее информационный объем 800 бит, содержит количество символов...

a)       10

b)       80

c)       100

d)       8

33.  В какой системе счисления хранится информация в компьютере?

a)       Троичной

b)       Двоичной

c)       Десятичной

d)       Двенадцатиричной

34. Сколько двоичных цифр можно записать в двух байтах?

a)       2

b)       8

c)       16

d)       32

 

Ключи к тесту:

1. e
2. c
3. d
4. c
5. b, c
6. d
7. b
8. a, e
9. b
10. d
11. d
12. c
13. e
14. d
15. b
16. a
17. d
18. c
19. d
20. b
21. b
22. a
23. c
24. c
25. d
26. a
27. b
28. c
29. d
30. c
31. d
32. c
33. b
34. c

 

 

 

 

4. Представление информации, языки, кодирование. Измерение информации. Объемный подход. Содержательный подход

         Из базового курса информатики вам известно:

 - Историческое развитие человека, формирование человеческого общества связано с развитием речи, с появлением и распространением языков. Язык — это знаковая система для представления и передачи информации.

 - Люди сохраняют свои знания в записях на различных носителях. Благодаря этому знания передаются не только в пространстве, но и во времени — от поколения к поколению.
 - Языки бывают естественные, например русский, китайский, английский, и формальные, например математическая символика, нотная грамота, языки программирования.

Письменность и кодирование информации

Под словом «кодирование» понимают процесс представления информации, удобный для ее хранения и/или передачи. Следовательно, запись текста на естественном языке можно рассматривать как способ кодирования речи с помощью графических элементов (букв, иероглифов). Записанный текст является кодом, заключающим в себе содержание речи, т. е. информацию.
Процесс чтения текста — это обратный по отношению к письму процесс, при котором письменный текст преобразуется в устную речь. Чтение можно назвать декодированием письменного текста. Схематически эти два процесса изображены на рис. 1.1.

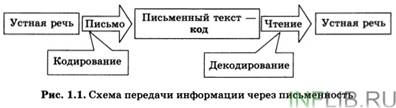
Схема на рис. 1.1 типична для всех процессов, связанных с передачей информации.

Цели и способы кодирования

А теперь обратим внимание на то, что может существовать много способов кодирования одного и того же текста на одном и том же языке. Например, русский текст мы привыкли записывать с помощью русского алфавита. Но то же самое можно сделать, используя латинский алфавит. Иногда так приходится поступать, отправляя SMS по мобильному телефону, на котором нет русских букв, или электронное письмо на русском языке за границу, если у адресата нет русифицированного программного обеспечения. Например, фразу «Здравствуй, дорогой Саша!» приходится писать так: «Zdravstvui, dorogoi Sasha!».

 

Существует множество способов кодирования. Например, стенография — быстрый способ записи устной речи. Ею владеют лишь немногие специально обученные люди — стенографисты. Они успевают записывать текст синхронно с речью выступающего человека. В стенограмме один значок обозначает целое слово или сочетание букв.

Расшифровать (декодировать) стенограмму может только сам стенографист.
Посмотрите на текст стенограммы на рис. 1.2.

Там написано следующее: «Говорить умеют все люди на свете. Даже у самых примитивных племен есть речь. Язык — это нечто всеобщее и самое человеческое, что есть на свете».

Можно придумать и другие способы кодирования.

Приведенные примеры иллюстрируют следующее важное правило: для кодирования одной и той же информации могут быть использованы разные способы; их выбор зависит от ряда обстоятельств: цели кодирования, условий, имеющихся средств.

Если надо записать текст в темпе речи, делаем это с помощью стенографии; если надо передать текст за границу, пользуемся латинским алфавитом; если надо представить текст в виде, понятном для грамотного русского человека, записываем его по правилам грамматики русского языка.

Еще одно важное обстоятельство: выбор способа кодирования информации может быть связан с предполагаемым способом ее обработки. Обсудим это на примере представления чисел — количественной информации. Используя русский алфавит, можно записать число «тридцать пять». Используя же алфавит арабской десятичной системы счисления, пишем: 35. Пусть вам надо произвести вычисления. Скажите, какая запись удобнее для выполнения расчетов: «тридцать пять умножить на сто двадцать семь» или «35 х 127»? Очевидно, что для перемножения многозначных чисел вы будете пользоваться второй записью.

Заметим, что две эти записи, эквивалентные по смыслу, используют разные языки: первая — естественный русский язык, вторая — формальный язык математики, не имеющий национальной принадлежности. Переход от представления на естественном языке к представлению на формальном языке можно также рассматривать как кодирование. Человеку удобно использовать для кодирования чисел десятичную систему счисления, а компьютеру — двоичную систему.

Широко используемыми в информатике формальными языками являются языки программирования.

В некоторых случаях возникает потребность засекречивания текста сообщения или документа, для того чтобы его не смогли прочитать те, кому не положено. Это называется защитой от несанкционированного доступа. В таком случае секретный текст шифруется. В давние времена шифрование называлось тайнописью. Шифрование представляет собой процесс превращения открытого текста в зашифрованный, а дешифрование — процесс обратного преобразования, при котором восстанавливается исходный текст.

 Шифрование — это тоже кодирование, но с засекреченным методом, известным только источнику и адресату. Методами шифрования занимается наука криптография.

История технических способов кодирования информации

С появлением технических средств хранения и передачи информации возникли новые идеи и приемы кодирования. Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в 1837 году американцем Сэмюэлем Морзе. Телеграфное сообщение — это последовательность электрических сигналов, передаваемая от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Эти технические обстоятельства привели Морзе к идее использования всего двух видов сигналов — короткого и длинного — для кодирования сообщения, передаваемого по линиям телеграфной связи.

Такой способ кодирования получил название азбуки Морзе. В ней каждая буква алфавита кодируется последовательностью коротких сигналов (точек) и длинных сигналов (тире). Буквы отделяются друг от друга паузами — отсутствием сигналов.

В таблице на рис. 1.3 показана азбука Морзе применительно к русскому алфавиту. Специальных знаков препинания в ней нет. Их обычно записывают словами: «тчк» — точка, «зпт» — запятая и т. п.

Самым знаменитым телеграфным сообщением является сигнал бедствия «SOS» (Save Our Souls — спасите наши души). Вот как он выглядит в коде азбуки Морзе: • • • - - - • • •
Три точки обозначают букву S, три тире — букву О. Две паузы отделяют буквы друг от друга.
Характерной особенностью азбуки Морзе является переменная длина кода разных букв, поэтому код Морзе называют неравномерным кодом. Буквы, которые встречаются в тексте чаще, имеют более короткий код, чем редкие буквы. Например, код буквы «Е» — одна точка, а код буквы «Ъ» состоит из шести знаков. Зачем так сделано? Чтобы сократить длину всего сообщения. Но из-за переменной длины кода букв возникает проблема отделения букв друг от друга в тексте. Поэтому приходится для разделения использовать паузу (пропуск). Следовательно, телеграфный алфавит Морзе является троичным, так как в нем используется три знака: точка, тире, пропуск.

Равномерный телеграфный код был изобретен французом Жаном Морисом Бодо в конце XIX века. В нем использовалось всего два вида сигналов. Неважно, как их назвать: точка и тире, плюс и минус, ноль и единица. Это два отличающихся друг от друга электрических сигнала.
В коде Бодо длина кодов всех символов алфавита одинакова и равна пяти. В таком случае не возникает проблемы отделения букв друг от друга: каждая пятерка сигналов — это знак текста.
Код Бодо — это первый в истории техники способ двоичного кодирования информации. Благодаря идее Бодо удалось автоматизировать процесс передачи и печати букв. Был создан клавишный телеграфный аппарат. Нажатие клавиши с определенной буквой вырабатывает соответствующий пятиимпульсный сигнал, который передается по линии связи. Принимающий аппарат под воздействием этого сигнала печатает ту же букву на бумажной ленте.
Из базового курса информатики вам известно, что в современных компьютерах для кодирования текстов также применяется равномерный двоичный код. Проблемы кодирования информации в компьютере и при передаче данных по сети мы рассмотрим несколько позже.

Вопрос об измерении количества информации является очень важным как для науки, так и для практики. В самом деле, информация является предметом нашей деятельности: мы ее храним, передаем, принимаем, обрабатываем. Поэтому важно договориться о способе ее измерения, позволяющем, например, ответить на вопросы: достаточно ли места на носителе, чтобы разместить нужную нам информацию, или сколько времени потребуется, чтобы передать ее по имеющемуся каналу связи. Величина, которая нас в этих ситуациях интересует, называется объемом информации. В таком случае говорят об объемном подходе к измерению информации.

Как измерить объем информации

Объем информации не связан с ее содержанием.

Когда говорят об объеме информации, то имеют в виду размер текста в том алфавите, с помощью которого эта информация представлена. Объем текста в печатном издании — книге, журнале, газете — обычно измеряют в страницах. В таком случае мы считаем, что, например, книга в 500 страниц содержит больше информации, чем книга в 250 страниц.

А как вы думаете, всегда ли книга в 500 страниц содержит в два раза больше информации, чем книга в 250 страниц? Конечно, нет! Ведь разные книги могут иметь разные форматы листов. Формат листа — это его стандартный размер. Существуют различные форматы печатного листа. Кроме того, разными бывают величина шрифта, длина строки, межстрочное расстояние. Очень часто детские книги печатаются крупным шрифтом с большими интервалами между строками, да еще и с большим количеством картинок. Зачастую содержание такой книги, состоящей из нескольких десятков страниц, можно перепечатать мелким шрифтом на 2-3 страницах. Но поскольку текст в обоих случаях один и тот же, то и количество информации должно быть одинаковым. Значит, измерение информации в страницах не является универсальным.

Количество страниц в печатном издании определяет расход бумаги, а не объем информации. Разумнее измерять объем информации, заключенный в тексте, количеством знаков этого текста. Знаки — это прежде всего буквы из алфавита того языка, на котором написана книга. Но в текст входят также и знаки препинания, скобки, цифры. В тексте могут использоваться буквы других алфавитов, например английского и греческого. Пробел между словами — тоже знак. Например, на странице формата А4 (21 см х 30 см) при размере шрифта (кегле), равном 12 пунктам (стандартным единицам), и одинарном интервале между строками помещается текст объемом примерно 4000 знаков. Определением объема информации в знаках часто пользуются в издательской практике. Например, журналисту может быть дано ограничение на объем статьи в 40 000 знаков.

Объемный способ измерения информации называют еще алфавитным подходом.

Объем информации в электронном сообщении

Выше мы говорили о телеграфном коде Бодо. В нем каждая буква алфавита кодируется пятизначным двоичным кодом. В русском алфавите 32 буквы (не считая буквы ё). Из базового курса информатики вы знаете, что если с помощью /-разрядного двоичного кода можно закодировать алфавит, состоящий из N символов, то эти величины связаны между собой по формуле:
2ⁱ = N.

Поскольку 2⁵ = 32, то все русские буквы можно закодировать всевозможными пятиразрядными двоичными кодами от 00000 до 11111. Русский телеграфный аппарат содержит 32 клавиши с буквами. Буква «ё» пропускается, вместо нее имеется более нужная клавиша «пробел». Знаки препинания передаются словами: «зпт», «тчк». Таким образом, телеграфный аппарат при вводе переводит русский текст в двоичный код, количество символов в котором в 5 раз больше, чем в исходном тексте.
Весь английский алфавит, состоящий из 26 букв, также можно закодировать пятиразрядным двоичным кодом. В отличие от русского алфавита, остается еще 6 свободных кодов, которые можно использовать для пробела и пяти знаков препинания.

Из базового курса информатики вам известно, что в компьютерах используется двоичное кодирование информации. Для двоичного представления текстов в компьютере чаще всего используется равномерный восьмиразрядный код. С его помощью можно закодировать алфавит из 256 символов, поскольку 256 = 2⁸. В стандартную кодовую таблицу (например, ASCII) помещаются все необходимые символы: английские и русские прописные и строчные буквы, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.
В двоичном коде один двоичный разряд несет одну единицу информации, которая называется 1 бит.
При двоичном кодировании объем информации, выраженный в битах, равен длине двоичного кода, в котором информация представлена.

Более крупной единицей измерения информации является байт: 1 байт = 8 битов.
Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству знаков в записи текста. Одна страница текста на листе формата А4 кегля 12 с одинарным интервалом между строками (см. пример выше) в компьютерном представлении будет иметь объем примерно 4000 байтов, так как на ней помещается примерно 4000 знаков.
Помимо бита и байта, для измерения информации используются и более крупные единицы:
1 Кб (килобайт) = 2¹⁰ байт = 1024 байта;

1 Мб (мегабайт) = 2¹⁰ Кб = 1024 Кб;

1 Гб (гигабайт) = 2¹⁰ Мб = 1024 Мб.

Объем той же страницы текста будет равным приблизительно 3,9 Кб. А книга из 500 таких страниц займет в памяти компьютера примерно 1,9 Мб.

Объемный подход к измерению информации используется для определения количества информации, заключенного в тексте, записанном с помощью некоторого алфавита. При этом содержательная сторона текста в учет не берется. Совершенно бессмысленное сочетание символов с данной позиции имеет ненулевой информационный объем.

 

Неопределенность знания и количество информации

Сейчас мы обсудим другой подход к измерению информации, который называют содержательным подходом. В этом случае количество информации связывается с содержанием (смыслом) полученного человеком сообщения. Вспомним, что с «человеческой» точки зрения информация — это знания, которые мы получаем из внешнего мира. Количество информации, заключенное в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.
Как же с этой точки зрения определяется единица измерения информации? Вы уже знаете, что эта единица называется битом. Проблема измерения информации исследована в теории информации, основатель которой — Клод Шеннон. В теории информации для бита дается следующее определение:

Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.
В этом определении есть понятия, которые требуют пояснения. Что такое неопределенность знания? Поясним на примерах. Допустим, вы бросаете монету, загадывая, что выпадет: орел или решка. Есть всего два возможных результата бросания монеты. Причем ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

В случае с монетой перед ее подбрасыванием неопределенность знания о результате равна двум. Игральный же кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знания о результате бросания кубика равна шести. Еще пример: спортсмены-лыжники перед забегом путем жеребьевки определяют свои порядковые номера на старте. Допустим, что имеется 100 участников соревнований, тогда неопределенность знания спортсмена о своем номере до жеребьевки равна 100.
Следовательно, можно сказать так:

Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, вытаскивание жребия и др.) — это количество возможных результатов.
Вернемся к примеру с монетой. После того как вы бросили монету и посмотрели на нее, вы получили зрительное сообщение, что выпал, например, орел. Определился один из двух возможных результатов. Неопределенность знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.
Сообщение об одном из двух равновероятных результатов некоторого события несет 1 бит информации.
Это утверждение — частный вывод из определения, данного выше.

А теперь такая задача: студент на экзамене может получить одну из четырех оценок: 5— «отлично», 4 — «хорошо», 3 — «удовлетворительно», 2 — «неудовлетворительно». Представьте себе, что ваш товарищ пошел сдавать экзамен. Причем учится он очень неровно и может с одинаковой вероятностью получить любую оценку от «2» до «5». Вы волнуетесь за него, ждете результата экзамена. Наконец, он пришел и на ваш вопрос: «Ну, что получил?» — ответил: «Четверку!».

Вопрос: сколько битов информации содержится в его ответе?

Если сразу сложно ответить на этот вопрос, то давайте подойдем к ответу постепенно. Будем отгадывать оценку, задавая вопросы, на которые можно ответить только «да» или «нет».
Вопросы будем ставить так, чтобы каждый ответ уменьшал количество возможных результатов в два раза и, следовательно, приносил 1 бит информации.

Первый вопрос:

 - Оценка выше «тройки»?

 - Да.

После этого ответа число вариантов уменьшилось в два раза. Остались только «4» и «5».

Получен 1 бит информации.

Второй вопрос:

 - Ты получил «пятерку»?

 - Нет.

Выбран один вариант из двух оставшихся: оценка — «четверка». Получен еще 1 бит информации. В сумме имеем 2 бита.

Сообщение об одном из четырех равновероятных результатов некоторого события несет 2 бита информации.

 

Главная формула информатики

А сейчас попробуем получить формулу, по которой вычисляется количество информации, содержащейся в сообщении о том, что имел место один из множества равновероятных результатов некоторого события.

Обозначим буквой N количество возможных результатов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов.

В примере с монетой: N = 2, i = 1 бит.

В примере с оценками: N = 4, i = 2 бита.

В примере со стеллажом: N = 8, i = 3 бита.

Нетрудно заметить, что связь между этими величинами выражается следующей формулой:
2ⁱ = N.

Действительно: 2¹ = 2 ; 2² = 4 ; 2³ = 8.

С полученной формулой вы уже знакомы из базового курса информатики, и еще не однажды мы с ней встретимся. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике оно называется показательным уравнением.
Пусть на стеллаже не 8, а 16 полок. Чтобы ответить на вопрос, сколько информации содержится в сообщении о месте нахождения книги, нужно решить уравнение:
2ⁱ= 16.

Поскольку 16 = 2⁴, то i = 4 бита.

Количество информации (i) содержащееся в сообщении об одном из N равновероятных результатов некоторого событий, определяется из решения показательного уравнения: 2ⁱ = N.
Если значение N равно целой степени двойки (4, 8,16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему, например, равно количество информации в сообщении о результате бросания игральной кости, у которой имеется шесть граней и, следовательно, N = 6? Можно догадаться, что решение уравнения
2ⁱ = 6 будет дробным числом, лежащим между 2 и 3, поскольку 2² = 4 < 6, а 2³ = 8 > 6. А как точнее узнать это число?

Пока ваших математических знаний недостаточно для того, чтобы решить это уравнение. Вы научитесь этому в 11-м классе в курсе математики. А сейчас сообщим, что результатом решения уравнения для N = 6 будет значение i = 2,58496 бита с точностью до пяти знаков после запятой.

 

 

Домашнее задание:

 

1. Составьте свою биографию, записав все числа (дата, месяц, год рождения; дата поступления в школу; дата поступлення в колледж) в двоичной системе счисления.

 

2. Переведите числа из двоичной системы счисления десятичную, в результате у вас  должен получиться  рисунок.

 

№ точки	Двоичная	Десятичная
1	(0110;1000)
2	(0111;1001)
3	(1010;1001)
4	(1011;1000)
5	(1011;0110)
6	(1010;0101)
7	(1101;0101)
8	(1110;0100)
9	(0101;0100)
10	(0011;0110)
11	(0010;0110)
12	(0010;0111)
13	(0011;0111)
14	(0011;1000)
15	(0100;1010)
16	(0111;1100)
17	(1010;1100)
18	(1100;1011)
19	(1101;1100)
20	(1100;1110)
21	(1100;10001)
22	(1110;1110)
23	(1110;1100)
24	(10000;1100)
25	(10001;1010)
26	(10001;1000)
27	(1111;0111)
28	(1110;0111)
29	(1010;0101)

 

 

 

 

 

 

 

 

 

 

Задача 1. В некоторой стране автомобильный номер длиной 6 символов составляют из заглавных букв (задействовано 19 различных букв) и десятичных цифр в любом порядке.

Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).

Определите объем памяти, отводимый этой программой для записи 40 номеров.

Варианты ответов:

1)      120 байт

2)      160 байт     

3)      200 байт          

4)      240 байт

Решение задачи:

1) в номере используется 19+10 = 29 символов.  

2) 2⁴ = 16 < 29 <= 2⁵ = 32. Поэтому для кодирования одного символа требуется

    5 бит.

3) в каждом номере – 6 символов. Поэтому для хранения одного номера нужно 30 бит.

4) так как 3*8 < 30 <= 4*8, то придется использовать 4 байт.

5) для записи 40 номеров нужно 4*40 = 160 байт.

 

Задача 2. В некоторой стране автомобильный номер длиной 7 символов составляют из заглавных букв (задействовано 25 различных букв) и десятичных цифр в любом порядке.

Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).

Определите объем памяти, отводимый этой программой для записи 40 номеров.

Варианты ответов:

1)      120 байт 

2)      160 байт

3)       200 байт      

4)       240 байт

 

Задача 3. В некоторой стране автомобильный номер длиной 10 символов составляют из заглавных букв (задействовано 19 различных букв) и десятичных цифр в любом порядке.

Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).

Определите объем памяти, отводимый этой программой для записи 40 номеров.

 Варианты ответов:

1)      160 байт        

2)      200 байт    

3)      240 байт    

4)      280 байт

Задача 4.  При регистрации в компьютерной системе, используемой при проведении командной олимпиады, каждому ученику выдается уникальный идентификатор  - целое число от 1 до  1000.  Для хранения каждого идентификатора используется одинаковое и минимально возможное количество бит.

В каждой команде участвует 4 ученика. Идентификатор команды состоит из последовательно записанных идентификаторов учеников и 12 дополнительных бит.

 Для записи каждого идентификатора команды система использует одинаковое и минимально возможное количество байт. 

 Сколько байт должна отвести система для записи идентификаторов 20 команд?

Варианты ответов:

1)      80 байт

2)      100 байт     

3)      120 байт          

4)      140 байт

Решение задачи:

1) Всего нужно 1000 вариантов идентификаторов учеников. Наименьшая степень двойки, которая больше или равна 1000, - это 2^10 = 1024. Поэтому минимальное количество бит, которое можно использовать для хранения одного идентификатора ученика – 10.

2) Для хранения идентификатора команды нужно 4×10 + 12 = 52 бит.

3) Далее, 52 бит = 6 байт + 4 бит. Поэтому наименьшее  целое  количество байт, достаточное для хранения одного идентификатора команды – 7.

4) Для хранения 20 идентификаторов нужно 20×7 = 140 байт.

 

Задача 5. При регистрации в компьютерной системе, используемой при проведении командной олимпиады, каждому ученику выдается уникальный идентификатор  - целое число от 1 до  1000.   Для хранения каждого идентификатора используется одинаковое и минимально возможное количество бит.

В каждой команде участвует 3 ученика. Идентификатор команды состоит из последовательно записанных идентификаторов учеников. Для записи каждого идентификатора команды система использует одинаковое и минимально возможное количество байт. 

 Сколько байт должна отвести система для записи идентификаторов 20 команд?

 Варианты ответов:

1)      80 байт        

2)      100 байт    

3)      120 байт    

4)      140 байт

 

Задача 6. При регистрации в компьютерной системе каждому пользователю выдается пароль,  состоящий из 9 символов и содержащий только символы A, B, C, D. E, F.

Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит).

Определите объем памяти, отводимый этой программой для записи 50 паролей.

Варианты ответов:

1)      200 байт        

2)      250 байт    

3)      300 байт    

4)      350 байт

 

Скачано с www.znanio.ru