Перевод систем счисления

Тема: Перевод небольших чисел из двоичной, восьмеричной и шестнадцатеричной системы счисления в десятичную.

Цель: на практики закрепить перевод из различных систем счислений и манипуляций над ними.

Задачи урока:

а) образовательные задачи - объяснить и закрепить новый материал, познакомить с историей открытия явления радиоактивности;

б) развивающие задачи - активизировать мыслительную деятельность учащихся на уроке, реализовать успешное овладение новым материалом, развивать речь, умение делать выводы;

в) воспитательные задачи - заинтересовать и увлечь темой урока, создать личную ситуацию успеха, вести коллективный поиск по сбору материала о радиации, создать условия для развития у школьников умения структурировать информацию.

Новый материал

шпаргалки заводить не обязательно, все и так делается на безусловном рефлексе. Но когда в сетях ковыряешься очень редко, то не всегда вспомнишь какая там маска в десятичной форме для префикса 21 или же какой адрес сети при этом же префиксе. В связи с этим я и решил написать несколько маленьких статей-шпаргалок по переводом чисел в различные системы счислений, сетевым адресам, маскам и т.п. В это части пойдет речь о переводи чисел в различные системы счислений.

1. Системы счислений

Когда вы занимаетесь чем-то связанным с компьютерными сетями и ИТ, вы по любому столкнетесь с этим понятием. И как толковый ИТ-шник вам нужно разбираться в этом хотя бы чу-чуть даже если на практике вы это будете применять очень редко.
Рассмотрим перевод каждой цифры из IP-адреса 98.251.16.138 в следующие системы счислений:

• Двоичная
• Восьмеричная
• Десятичная
• Шестнадцатеричная

1.1 Десятичная

Так как цифры записаны в десятичной, перевод с десятичной в десятичную пропустим 🙂

1.1.1 Десятичная → Двоичная

Как мы знаем двоичная система счисления используется практически во всех современных компьютерах и многих других вычислительных устройствах. Система очень проста – у нас есть только 0 и 1.
Для преобразования числа с десятиной в двоичную форму нужно использовать деление по модулю 2 (т.е. целочисленное деление на 2) в результате чего мы всегда будем иметь в остатке либо 1, либо 0. При этом результат записываем справа налево. Пример все поставит на свои места:

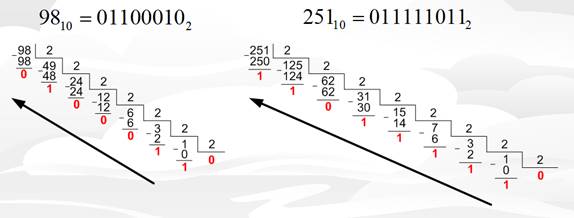
Рисунок 1.1 – Перевод чисел из десятичной в двоичную систему

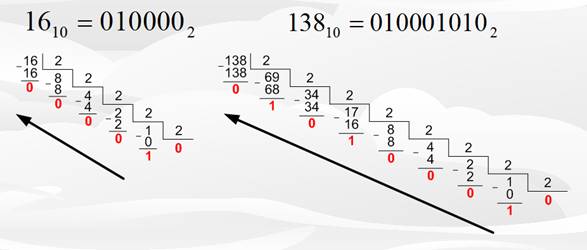
Рисунок 1.2 – Перевод чисел из десятичной в двоичную систему

Опишу деление числа 98. Мы делим 98 на 2, в результате имеем 49 и остаток 0. Далее продолжаем деление и делим 49 на 2, в результате имеем 24 с остатком 1. И таким же образом добираемся до 1-ки или 0-ка в делимом. Затем результат записываем справа налево.

1.1.2 Десятичная → Восьмеричная

Восьмеричная система – это целочисленная система счисления с основанием 8. Т.е. все числа в ней представлены диапазоном 0 – 7 и для перевода с десятичной системы нужно использовать деление по модулю 8.

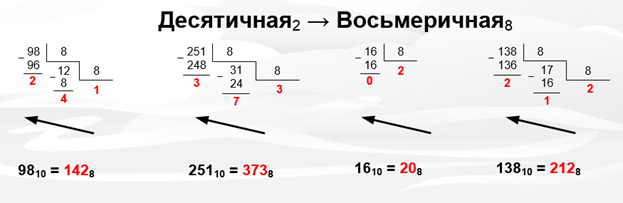
Рисунок 1.3 – Перевод чисел из десятичной в восьмеричную систему

Деление аналогично 2-чной системе.

1.1.3 Десятичная → Шестнадцатеричная

Шестнадцатеричная система почти полностью вытеснила восьмеричную систему. У нее основание 16, но используются десятичные цифры от 0 до 9 + латинские буквы от A(число 10) до F(число 15). С ней вы сталкиваетесь каждый раз, когда проверяете настройки сетевого адаптера — это МАС-адрес. Так же, когда используется IPv6.

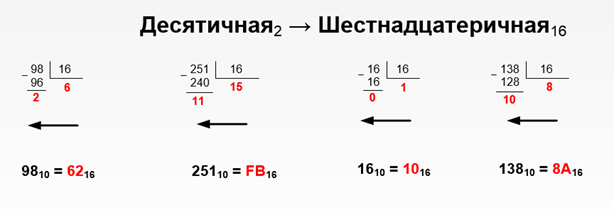
Рисунок 1.4 – Перевод чисел из десятичной в шестнадцатеричную систему

1.2 Двоичная

В предыдущем примере мы перевели все десятичные числа в другие системы счислений, одна из которых двоичная. Теперь переведем каждое число с двоичной формы.

1.2.1 Двоичная → Десятичная

Для перевода чисел с двоичной формы в десятичную нужно знать два нюанса. Первый – у каждого нолика и единички есть множитель 2 в n-й степени, при котором n увеличивается справа налево ровно на единичку. Второй – после перемножения все числа нужно сложить и мы получим число в десятичной форме. В итого у нас будет формула такого вида:

D = (a_n × p^n-1) + (a_n-1 × p^n-2) + (a_n-2 × p^n-3) +…, (1.2.1)

Где,
D – это число в десятичной форме, которое мы ищем;
n – количество символов в двоичном числе;
a – число в двоичной форме на n-й позиции (т.е. первый символ, второй, и т.п.);
p – коэффициент, равный 2,8 или 16 в степени n (в зависимости от системы счисления)

К примеру возьмем число 110102. Смотрим на формулу и записываем:

• Число состоит из 5 символов (n=5)
• a₅ = 1, a₄ = 1, a₃ = 0, a₂ = 1, a₁ = 0
• p = 2 (так как переводим из двоичной в десятичную)

В итоге имеем:

D = (1 × 2^5-1) + (1 × 2^5-2) + (0 × 2^5-3) + (1 × 2^5-4) + (0 × 2^5-5) = 16 + 8 + 0 + 2 + 0 = 26₁₀

Кто привык записывать справа на лево, форму будет выглядеть так:

D = (0 × 2^5-5) + (1 × 2^5-4) + (0 × 2^5-3) + (1 × 2^5-2) + (1 × 2^5-1) = 0 + 2 + 0 + 8 + 16 = 26₁₀

Но, как мы знаем, от перестановки слагаемых сумма не меняется. Давайте теперь переведем наши числа в десятичную форму.

Рисунок 1.5 – Перевод чисел из двоичной в десятичную систему

1.2.2 Двоичная → Восьмеричная

При переводе нам нужно двоичное число разбить на группы по три символа справа налево. Если последняя группа не состоит из трех символов, то мы просто возмещаем недостающие биты ноликами. К примеру:

10101001 = 010 101 001

1011100 = 001 011 100

Каждая группа битов – это одно из восьмеричных чисел. Чтобы узнать какое, нужно использовать написанную выше формулу 1.2.1 для каждой группы битов. В результате мы получим.

Рисунок 1.6 – Перевод чисел из двоичной в восьмеричную систему

1.2.3 Двоичная → Шестнадцатеричная

Здесь нам нужно двоичное число разбивать на группы по четыре символа справа налево с последующим дополнением недостающих битов группы ноликами, как писалось выше. Если последняя группа состоит из ноликов, то их нужно игнорировать.

110101011 = 0001 1010 1011

1011100 = 0101 1100

001010000 = 000101 0000 = 0101 0000

Каждая группа битов – это одно из шестнадцатеричных чисел. Используем формулу 1.2.1 для каждой группы битов.

Рисунок 1.7 – Перевод чисел из двоичной в шестнадцатеричную систему

1.3 Восьмеричная

В этой системе у нас могут возникнуть сложности только при переводе в 16-ричную систему, так как остальной перевод проходит гладко.

1.3.1 Восьмеричная → Двоичная

Каждое число в восьмеричной системе – это группа из трех битов в двоичной системе, как писалось выше. Для перевода нам нужно воспользоваться табличкой-шпаргалкой:

Рисунок 1.8 – Шпора по переводу чисел из восьмеричной системы

Используя эту табличку переведем наши числа в двоичную систему.

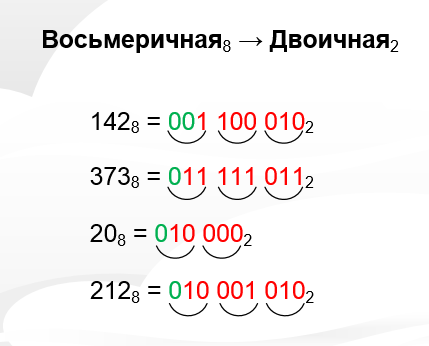
Рисунок 1.9 – Перевод чисел из восьмеричной в двоичную систему

Немного опишу вывод. Первое число у нас 142, значит будет три группы по три бита в каждой. Юзаем шпору и видим, что цифра 1 это 001, цифра 4 это 100 и цифра 2 это 010. В результате имеем число 001100010.

1.3.2 Восьмеричная → Десятичная

Здесь мы используем формулу 1.2.1 только с коэффициентом 8 (т.е. p=8). В результате имеем

Рисунок 1.10 – Перевод чисел из восьмеричной в десятеричную систему

Возьмем первое число. Исходя из формулы 1.2.1:

• Число состоит из 3 символов (n=3)
• a₃ = 1, a₂ = 4, a₁ = 2
• p = 8 (так как переводим из восьмеричной в десятичную)

В результате имеем:

D = (1 × 8^3-1) + (4 × 8^3-2) + (2 × 8^3-3) = 64 + 32 + 2 = 98₁₀

1.3.3 Восьмеричная → Шестнадцатеричная

Как писалось раньше, для перевода нам нужно сначала перевести числа в двоичную систему, потом с двоичной в шестнадцатеричную, поделив на группы по 4-ре бита. Можно использовать следующею шпору.

Рисунок 1.11 – Шпора по переводу чисел из шестнадцатеричной системы

Эта табличка поможет перевести из двоичной в шестнадцатеричную систему. Теперь переведем наши числа.

Рисунок 1.12 – Перевод чисел из восьмеричной в шестнадцатеричную систему

1.4 Шестнадцатеричная

В этой системе та же проблема, при переводе в восьмеричную. Но об этом позже.

1.4.1 Шестнадцатеричная → Двоичная

Каждое число в шестнадцатеричной системе – это группа из четырех битов в двоичной системе, как писалось выше. Для перевода нам можно воспользоваться табличкой-шпаргалкой, которая находиться выше. В результате:

Рисунок 1.13 – Перевод чисел из шестнадцатеричной в двоичную систему

Возьмем первое число – 62. Используя табличку (рис. 1.11) мы видим, что 6 это 0110, 2 это 0010, в результате имеем число 01100010.

1.4.2 Шестнадцатеричная → Десятичная

Здесь мы используем формулу 1.2.1 только с коэффициентом 16 (т.е. p=16). В результате имеем

Рисунок 1.14 – Перевод чисел из шестнадцатеричной в десятеричную систему

Возьмем первое число. Исходя из формулы 1.2.1:

• Число состоит из 2 символов (n=2)
• a₂ = 6, a₁ = 2
• p = 16 (так как переводим из шестнадцатеричной в десятичную)

В результате имеем.

D = (6 × 16^2-1) + (2 × 16^2-2) = 96 + 2 = 98₁₀

1.4.3 Шестнадцатеричная → Восьмеричная

Для перевода в восьмеричную систему нужно сначала перевести в двоичную, затем разбить на группы по 3-и бита и воспользоваться табличкой (рис. 1.8). В результате:

Рисунок 1.15 – Перевод чисел из шестнадцатеричной в восьмеричную систему

Домашнее задание: Изучить конспект, параграф № 1,

Скачано с www.znanio.ru