Для преподавателей

АЛГЕБРА

ПОУРОЧНЫЕ ПЛАНЫ

по учебнику

Ю. Н. Макарычева, Н. Г. Миндюк, К. И. Нешкова, С. Б. Суворовой

класс

Издательство «Учитель»

АЛГЕБРА

9 КЛАСС

ПОУРОЧНЫЕ ПЛАНЫ

по учебнику Ю. Н. Макарычева,

Н. Г. Миндюк, К. И. Нешкова, С. Б. Суворовой

Автор-составитель С. П. Ковалева

2-е издание, стереотипное

Волгоград

удк 371.214.1

ББК 74.262.21

А45

Автор-составитель С. П. Ковалева

Алгебра. 9 кл.: поурочные планы по учебнику Ю. Н. МаА 45 карычева и др. / авт.-сост. С. П. Ковалева. — 2-е изд., стереотип.

Волгоград: Учитель, 2008. — 316 с.

ISBN 978-5-7057-0666-2

В данном пособии представлено примерное поурочное планирование, составленное в СООТВСТСТВИИ с учебником: Макарычев Ю. Н., Минлок Н. Г.. Нешков К. И Суворова С. Б. Алгебра—9. М.: Просвещение, 2005. В разработках ПЛшЮВ уроков содержится теоретический материал курса алгебры 9 класса, даются примеры, задачи и рассматриваются способы их решения, предлагаются задания для самостоятельной и индивидуальной работы учащихся, а также контрольные работы, тесты. Дополнительно приводятся начальные сведения из теории вероятностей, решения комбинаторных задач.

Пособие предназначено учителям-предметникам в помощь при подготовке и проведении уроков математики в 9 классе общеобразовательной школы. Может быть полезно студентам педагогических вузов, слушателям ИК К.

удк 371.214.l

ББК 74.262.21

ISBN 978-5-7057-0666-2 С) Ковалева С. П., автор-составитель, 2005 (Ф Издагельство «УЧИТСЈП,», 2005

© Оформление. Издательство «Учитель», 2005

Последнее издание, 2008

ВВЕДТШЕ

В пособии представлены поурочные планы по курсу алгебры 9 класса, составленные в соответствии с программой Министерства образования (по учебнику «Алгебра—9» Ю. Н. Макарычева и др. М.: Просвещение, 2005).

Целью данного пособия является практическая помощь учитето, особенно начинающему, в выборе путей построения урока, отвечающего современным требованиям. Планирование дается из расчета З часа в неделю (всего 102 часа в год).

В пособии кратко излагается основной теоретический материал, даются примеры, задачи и разбираются способы их решения, предлагаются диктанты, самостоятельные и индивидуальные задания, контрольные работы и тесты, а также карточки для устного и письменного опросов. Использованы задания для подготовки к итоговой аттестации.

Рассмотрен материал из комбинаторики и теории вероятности (изложены основные моменты теории, предложены тренировочные упражнения).

Пособие предназначено для учителей-предметников в помощь при планировании уроков.

Примерное поурочное планирование по алгебре в 9 классе

(З часа в неделю — 102 часа за год)

•       Алгебра-9: учебник / авт.: Ю. Н. Макарычев и др. М.: Просвещение, 2003 [2] *

•       Алгебра: сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 ка. / авт.: Л. В. Кузнецова и др. М.: Дрофа, 2002[4]*.

[4] — см. по тексту: Литература, с. 312.

Продолжение табл.

Окончание тао.7.

Глава 1. КВАДРАТИЧНАЯ ФУНКЦИЯ (25 часов)

 1. ФУНКЦИИ И ИХ СВОЙСТВА

Тема (п. 1): ФУНКЦИЯ. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ (3 ч)

Цели: систематизировать и расширить представления о функциях; выработать умение находить значения функции по заданным значениям аргумента и значения аргумента по значениям функции; выработать умения находить область определения и область значений функции; отработать умения строить графики линейной функции, прямой и обратной пропорциональностей.

Урок 1

Ход урока

1. Объяснение нового материала.

1. Вводная беседа.

Слово «функция» в математике появилось сравнительно недавно. Впервые о функциях стал говорить великий немецкий математик и философ Г. В. Лейбниц в конце XVII века, а первое определение функции дал, вероятно, его ученик И. Бернулли в l718 году. Впрочем, это было не то определение, которым мы пользуемся сегодня. Определение функций было дано позднее — в конце XLX века.

О функциях говорят не только в теоретических дисциплинах. Без них не обойтись ни финансисту, ни социологу, ни даже просто

читателю газет — в любой газете можно встретить диаграмму или график, и любой человек должен уметь их понимать без излишней траты умственных сил.

Понятие функции — это очень общее понятие, с которым мы встречаемся на каждом шагу, не всегда даже отдавая себе в этом отчет. Приведем при мер ы : 1) Каждому многоугольнику поставим в соответствие число, равное его площади. 2) Каждому слову русского языка поставим в соответствие его первую букву. Именно так поступают при составлении словарей. З) Каждому человеку поставим в соответствие его группу крови.

Нас окружает множество изменяющихся величин. Изменяется скорость движущихся автомашин и летящих самолетов, меняется высота солнца над горизонтом и положение планет на их орбитах, изменяется температура воздуха, сила ветра и величина атмосферного давлении и т. д. Многообразие меняющихся величин очень велико. Некоторые из этих величин очень тесно связаны между собой. В дальнейшем будем изучать только такие переменные величины, между которыми существуют зависимости, позволяющие определить единственное значение одной из них, как только станут известны значения остальных.

Современный человек живет в меняющемся мире, мире связей и зависимостей, а лучшего способа их выразить, чем функции и графики, нет.

2. Даются определения функции, независимой и зависимой переменных, области определения и области значений функции, графика функции.

З. Рассматривается при ме р : найти область определения функцииЛх) =

Решение:

       3) 5-2х20 х^з I

2,5

Ответ: ДО) =  2,5].

4. Рассматривается та бл и ца «Графики элементарных функций»:

11. Закрепление изучаемого материала.

1.  № 1, 2, 50, в), 6, 7(а, в) [2].

2.  Устные упражнения.

№ 1. Функция задана формулойЛх) = —х² + 5. Найдите значения функции при х = —1;

Ответ: 4; 2,75; —4.

№ 2. Найдите область определения функции:

2х + 4 Ответ: а)Д(у) = R, б)Д(у) = [О; +00);

в) до =    -2)U    +0). Ш. Повторение.

Решить № 22 (б, в).

IV. Итоги урока.

Вопросы учащимся:

1)   Что называется функцией?

2)   Что называется областью определения функции? З) Что называется областью значений функции? Домашнее задание: п. 1, № З, 8, 1, 22 (а) [2].

Урок 2

Ход урока

1. Проверка домашней работы.

Фронтальная устная проверка домашней работы.

П. Индивидуальные задания.

КАРТОЧКА

1.   ,5) для функции, заданной формулой:

3х

       а)Лх) =        ; 6)f(x) = 2х² + х— З.

          ответ: а)Л0) -0, лз)^е = 2,5;                    9;

                     6)Л0) = -3;            52; Л-1,5) = о.

2.   Найдите область определения функции, заданной формулой:

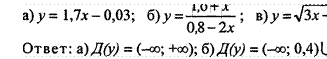(0,4; +ф).,

в) ДО) =

КАРТОЧКА 2

1 . Функция задана формулойЛх) = х² + х. Найдите:

а)Л0)•, 6)Л-1)•, в) 4 +Л-З).

         Ответ: а) ЛО) = 0;  в) 4                  10.

2. Найдите значения х, при которыхр(х) = 0, если:

        а)р(х) = 2х +4; б)р(х) = (2х +            + 3); в)р(х) = (2х +            .

Ответ: а) —2; б) —2; в) —2; О.

КАРТОЧКА З

1 . Функция задана формулойЛх) = х² — 2. Найдите:

47

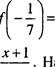        Ответ:          , 1) = —1,99;               +f

49

2. Функция задана формулой g(x) = Найдите значения х, x—l при которых: а) g(x) = 1; б) g(x) = 0; в) g(x) = —1; г) g(x) = 1,5.

Ответ: а) нет таких значений х; б) —1; в) 0; г) 5.

Ш. Устный фронтальный опрос.

Вопросы учащимся:

1)                     Что называется функцией?

2)                     Какую переменную называют независимой, какую зависимой? Что называется аргументом функции?

3)                     Что называется областью определения, областью значений функции?

4)                     Определение графика функции.

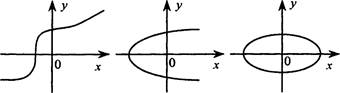
IV. Устные упражнения по готовым рисункам.

На рисунках (см. рис. а—з, с. 11) приведены различные кривые. Какие их них являются графиками функций? Почему?

а)                        б)   в)         г) у

Ответ: б), д), е), з).

V.    Решение упражнений. № 9, 13 (а, б, г).

VI. Итоги урока. Решить устно № 10, 16.

Домашнее задание: п. 1, № 13 (в), 14, 17 [2].

Урок З

Ход урока

1. Проверка домашней работы.

1.  Решение у доски № 17.

2.  Устная проверка № 14.

З. Ответы на вопросы учащихся.

II. Устные упражнения.

Выполнить устно задания. Ответы записать в тетрадь.

№ 1. Функция задана формулойЛх) = 2х•(З — х). Найдите значение функции, соответствующее значению аргумента, равному:

а) о; 6) -3; в) 1,5.

№ 2. Найдите область определения функции:

2

а) у = 37х— 1; б) у =

— х² —1

П ро верка ответов:

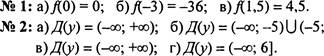 +ф).,

111. Решение упражнений. № 18 (а).

IV. Повторение.

1.   Повторить формулы дискриминанта и корней квадратного

уравнения.

2.   Решить № 23 (а, в).

V. Самостоятельная работа.

Домашнее задание: п. 1, № 20, 23 (6, г)

Тема (п. 2): СВОЙСТВА ФУНКЦИЙ (3 ч)

Цели: расширить представления о функциях, ввести понятия нулей функции, возрастающей и убывающей функций в промежутке; сформировать умения находить по графику нули функции, промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет свой знак.

12

Урок 4

Ход урока

1. Анализ ошибок самостоятельной работы.

11. Изучение нового материала.

1. Учащимся предлагается ответить на вопрос ы (можно использовать график функции у =f(x), изображенный на рисунке):

1)                       Что называется областью определения функции? Найдите область определения данной функции.

2)                       Что называется областью значений функции? Назовите область значений данной функции.

З) Назовите значения аргумента, при которых функция обращается в нуль.

4)    Сформулируйте определение нулей функции.

5)    Назовите промежутки, в которых функция принимает положительные, отрицательные значения.

6)    Дайте понятие промежутков знакопостоянства.

7)    Сформулируйте определения возрастающей, убывающей функций в некотором промежутке.

8)    Используя рисунок, назовите промежутки возрастания и убывания функции.

2. Учащимся предлагается составить схему исследования функций.

С х ем а исследования функций:

) Найти область определения функции.

2) Найти область значений функции.

З) Найти нули функции.

4)   Найти промежутки знакопостоянства функции.

5)   Найти промежутки возрастания и убывания функции.

З. Предложить учащимся назвать функции, которые возрастают, убывают на всей области определения (можно использовать таблицу «Графики элементарных функций» — см. урок 1, с. 8).

4. Дать определение возрастающей, убывающей функций.

Ш. Закрепление изучаемого материала.

1.   Решить № 24 (устно).

2.   Решить№ 26, 29, 31.

З. По схеме исследовать функцию, график которой изображен на рис. 10 [2, с. l l ] — устно. IV. Повторение. № 41 (а, б). У. Итоги урока.

Самостоятельная работа обучающего характера с последующей проверкой. Двое учащихся выполняют задание на закрытых досках.

ВАРИАНТ

Постройте график какой-либо функции, областью определения которой служит промежуток [—2; 6], а областью значений — промежуток [—4; З]. Опишите свойства этой функции.

ВАРИАНТ П

Постройте график какой-либо функции, областью определения которой служит промежуток [—6; 6], а областью значений — промежуток [—4; 4]. Опишите свойства этой функции.

Домашнее задание: п. 2, № 25, 28, 30, 32, 41 (в) [2].

Урок 5

Ход урока

1. Проверка домашней работы.

Ответы на вопросы учащихся.

11. Устные упражнения.

1.    Решить № 27.

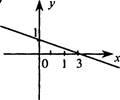
2.    Какие из графиков функций, задаваемых формулами у =—,

х

х                                                           з  х^х , у = ^Е — 1, изображены на

З х З з з рисунках (см. рис. а—ж, с. 15)?

ххх

г)Д)

                                                       х

3.    Назовите возрастающие (убывающие) функции. Ответ объ-

ясните.

Ш. Изучение нового материала.

Диалог с учащимися.

1)                    Рассмотрим функцию у = Кх + 6 (К > 0).

2)                    Что называется областью определения функции? Какова область определения данной функции?

З) Что называется областью значений функции? Найдите область значений данной функции.

4)    Дайте определение нулей функции. Как найти нуль данной функции? Объясните.

5)    Как найти промежутки, в которых функция у = К.х + в (К > О) принимает положительные, отрицательные значения?

6)    Какая функция называется возрастающей (убывающей) в промежутке?

7)    Докажем, что функция у = Кх + в (К > 0) является возрастающей.

Аналогично рассматриваются свойства функции у = —(00).

х

Можно предложить учащимся самостоятел ь но описать

К свойства функций у = Кх + в, у

х

Конспект нового материала

Линейная функция у -Кх + в(К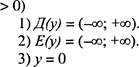У = Кх + в (К < О)

кх + з=о Кх =

= — ² — нуль функции. х

Кх + в > О

Кх >

0 при х > —— К

        У       при х<—— .

5) Дано: у = Кх+ в (К Доказать: у = Кх + в (К > О) — возрастающая функция.

Доказательство: Пусть И Х2 — произвольные значения аргумента и > „Ч.

= кх2 + в, у: = Км + в

У2 — у 1 = (кх2 + в) — (kXl + в) =

= кх2 + в ,kXl — в = Кх, — kXl =

= К(Х2 Xl)

К > 0 (по условию)

           у        при х<——

           У        при х

5) Дано: у = кх + в (К

Доказать: у = Кх + в (К < 0) — , убывающая функция.

, Доказательство: Пусть и — произвольные  значения аргумента и > М.

= кх2 + в, = Кл + в

У2 — уп = (к.х2 + в) — (Ки + в) =  = кх2 + в — Км — в = кх2 — Клэ =

= К(Х2 —Xl)

К < 0 (по условию)

Следовательно, к(х2 — .xD > О.  Следовательно, К(Х2 — Х!) < О

Тогда» -- у > 0. Значит, _У2 >Yl• ' Тогда П — у Значит, № <Yl. Тогда данная функция является Тогда данная функция являетвозрастающей: • ся убывающей:

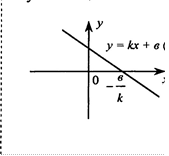у = Кх + в (К > О) х

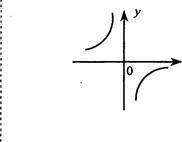
Обратная пропорциональность

                         х                                                       х

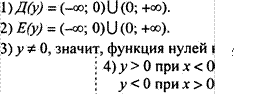
0 при х у при х < О.

5) Функция убывающая                ' 5) Функция возрастающая

х

IV. Закрепление изученного материала. № 33, 34, 35.

V.    Повторение. № 42.

VI. Итоги урока.

Привести примеры возрастающей и убывающей функций.

Домашнее задание: п. 2, контрольные вопросы [2, с. 16, 17] № 37, 152, 157.

Урок 6

Ход урока

1. Проверка домашпсй работы.

1.   Решить № 152 устно.

2r+l l

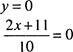
2x + l l = O 2x = -l l х = —5,5 — нуль

функции.

2.   Решить № свойства. 6 х

    Если        О, тоу

       6                             3х ² -12

                   8 -0,5х                                  4

При любом значе- нии х из области 3х-2 -12 определения функ- 4

ции у 0. Следова- 3.r“ — 12-0 тельно, нули функ-- 12

ции не существуют.

 нули функции.

157. Постройте график функции и ОПИШИТе ее

6

х

6 Если х < 0, то у

х

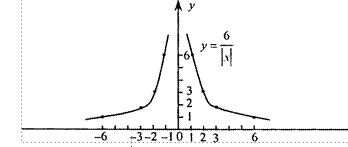
(0, +00).

З) Нулей функции нет.

             О при х е (—с,              (0; +00).

5) Функция возрастает на (—с, 0); функция убывает на (0; +o).

П. Тренировочные упражнения.

Т ес т (с последующей проверкой, анализом ошибок).

ВАРИАНТ (11)

1.   Функция у = З 5х принимает отрицательные (положительные) значения, если х принадлежит промежутку:

1)       2) (—оо; 0,6]; З) (0,6; +o); 4)

2.   Функция у = 3х — 5 принимает положительные (отрицательные) значения, если х принадлежит промежутку:

1)      -оо;1 ²3 ), 2)         + 00     З) 1L,.+oo • 4) -oo;l— .

З. Если функция возрастающая (убывающая), то:

2)Л2) >Л-З)•, 3)Л3) $5); 4)Л2) <Л-З).

4.  Если Л2) <Л1), (ЛЗ) >Л4)), то функция:

) возрастающая; 2) убывающая.

5.  Какие из функций являются возрастающими (убывающими)

Ответы :

                            Вариант                    Вариант П

                                               1. 4)

ВАРИАНТ Ш

1 . Функция задана формулой у = 3х² — 4. Найдите у(З).

1) 14; 2) 23; 3) 24; 4) 27.

2. Функция задана формулой у = —3,5х + 7. Найдите такое значение х, при которомЛх) = О: 1) 2; 2) -2, 3) о, 4) 0,2.

19

З. Найдите область определения функции, заданной формулой

5-х

4. Определите, при каких значениях х существует функция, заданная формулой у .

      1)          -12); 2) [-12, +0); 3)          -121; 4) [0; +о.

5. Найдите область значений функции у = 2х² + 1.

ответы: 1. 2) 2. 1) 3. 2) 4. 2) 5. 2) Ш. Закрепление изученного материала.

№ 36; 38 — устно.

№ 36.

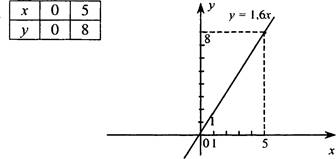
— 1,6х — прямая пропорциональность, график — прямая.

= —0 4х— прямая пропорциональность, график — прямая.

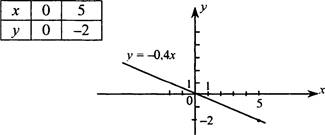
У = Кл, К > О

2) х = 0 — нуль функции;

0 прих> О; у при х < О;

4) функция возрастающая.

IV. Итоги урока.

I . Решить № 153 — устно.

У = Кх, К < О

2) х = 0 — нуль функции;

0 при х<О;

      У            при х > О;

4) функция убывающая.

2. Контрольные вопросы [2, с. 16, 17]. № 153.

а) у = —0,01х — убывающая функция, так как К = —0,01 < О;

б) у = 16х — возрастающая функция, так как К = 16 > О;

в) у =—х+ З — возрастающая функция, так как К =— > О 7

г) у = 13 — х — убывающая функция, так как К = —1 < О

Домашнее задание: п. 2, № 39, 40, 155, 156 [2].

Тема (п. 3): КВАДРАТНЫЙ ТРЕХЧЛЕН И ЕГО КОРНИ (1 ч)

Цели: ввести понятия квадратного трехчлена, корней квадратного трехчлена; закрепить умения находить дискриминант и корни квадратного трехчлена; особое внимание уделить задачам, связанным с выделением квадрата двучлена из квадратного трехчлена.

Урок 7

Ход урока

1. Проверка домашней работы.

1.  Устная проверка решения № 155, 156.

2.  Ответы на вопросы учащихся.

11. Проверка знаний учащихся. Самостоятельная работа.

ВАРИАНТ

№ 1 . Выясните свойства функции:

25

х

№ 2. Найдите нули функции (если они существуют):

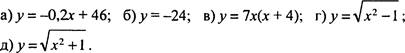
ВАРИАНТ

№ 1. Выясните свойства функции:

36

25х- 18;

№ 2. Найдите нули функции (если они существуют):

- -0,4х+ 32,

ј7Г4.

Решение:

Вариант

25

1) ДО) = Е(у) =     (0; +00); 2) у * 0, нулей функции нет;

4) функция убывающая. х = — Д — нуль функции;

4

     З)у> 0 при х        l ^L

4

28х+35

28х > -35

35

28

4 при х <— Д;

4 4) так как К = 28 > 0, то функция возрастающая.

а) =               + 46, У = О

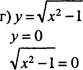-0,2х + 46 = о —0,2х = -46 х = 230 нуль функции; х² —1 = О x2- l =O

б) у = —24 — нулей функции нет; х — нули функции;

в) у = 7х(х + 4)                                  

у 0, так как при любом 7х(х + 4) = О    значении х х² + > 0, нулей х = 0 или х +4=0 функции нет. х = 0 или х = -4 — нули функции;

От в е т: а) 230; б) нулей функции нет; в) -4; 0; г) —1; 1; д) нулей функции нет.

Вариант П

36

х

= Е(у) = +0;

18

З)у> 0 при х

25

25х- 18>O

25х> 18

18

25

18 . у < 0 при х <—— 25

4) так как К 25 > О, то функция возрастающая.

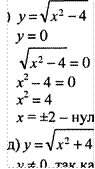а) у: -0,4х + 32

—0,4х + 32 = О

х = 80 — нуль функции;

б) у = 47 — нулей функции нет;

— нули функции;

в) у = 9х(х — 5)

у 0, так как при любом зна9х(х - 5) = о чениих .х² + 4 > О, нулей функх = О или х —5 = О ции нет. х = 0 или х = 5 — нули функции;

Ответ: а) 80; б) нулей функции нет; в) 0; 5; г) —2; 2; д) нулей функции нет.

После выполнения работы проверить решение и ответы заданий (можно использовать заранее приготовленные записи или тсо).

111. Изучение нового материала.

1.                     Ввести понятия квадратного трехчлена, корня квадратного трехчлена, дискриминанта квадратного трехчлена.

2.                     Рассмотреть п р и мер ы .

Выделить из трехчлена: а) 2х² —4х + 6; б) 3х² — 36х + 140 квадрат двучлена (пример 2) [2, с. 18]. Решение:

а) 2х² -4х+6= 2(х² -2х+ 3) = 26² -2х+    + 3) = =  + 2) = 20- +4.

IV. Закрепление нового материала.

Задания — по вариантам, проверка решения — у доски. ВАРИАНТ 1. № 43 (число З —0 ), № 44 (г, е), 48 (в).

ВАРИАНТ 11. № 43 (число —7 +0 ), № 44 (в, д), 48 (г).

Решение:

+2-18+60 +7=0.

Число З —С2 является корнем квадратного трехчленах² 6х + 7.

х2 — 6х + 7

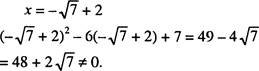 +4+6 ф-

Число —0 +2 не является корнем квадратного трехчлена х² — 6х +7.

П. Найдем корни квадратного трехчлена х² — 6х + 7. х- — 6х + 7

д -9-7=2

а

     Числа З            являются корнями данного квадратного трехчлена.

Отв е т: число З —0— корень квадратного трехчлена; число + 2 не является корнем квадратного трехчлена.

№ 44 (в, г, д, е).

  в) 0,2х² + 3х — 20              г) -2x² -x-O,125

           0,2х² + 3х - 20 = о                      -2х² -x-O,125 = о

         Д = в² — 4ас                                2х² + х + 0,125 = о

                                25                          

х=—— 4 '

2а

0,4

= -20,

д) 0, 1х² + 0,4

0,1х² +        = о 0, 1х2 = —0,4

решения нет, квадратный трехчлен не имеет корней;

е) —0,3х² + 1,5х

-0,3х² + 1,5х = о

х = 0 или х— 5=0 х = 0 или х = 5.

Ответ: в) —20; 5; г) —1 ; д) корней нет; е) 0; 5. 4

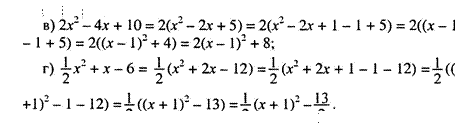2  2 V. Итоги урока.

Устный опрос, устн ы е упражне н и я

1.  Что называется квадратным трехчленом?

2.  Назовите квадратные трехчлены:

1)  3х²6) ах² +6х+с, а * О;

2)  2х- 1; 7) 10х² + З;

3)  5х² - 7х•,            8) 7х² + 5х + з;

4)  ах- + вх, а О;            9) ах- + вх;

5)  вх+ с, в $0;   10) ах² + с, а * 0.

3. Дайте определение корня квадратного трехчлена.

Домашнее задание: п. 3, № 44 (а, б), 45, 47, 49 [2, с. 243, 244] (с. 17—20 — повторить).

Тема (п. 4): РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЕХЧЛЕНА НА МНОЖИТЕЛИ (3 ч)

Цели: доказать теорему о разложении квадратного трехчлена на множители; сформировать умения раскладывать квадратный трехчлен на множители; выработать умения выделять квадрат двучлена при решении задач.

Урок 8

Ход урока

1. Организационный момент.

Итоги самостоятельной работы, вопросы по домашней работе.

11. Устные упражнения.

. Найдите корни квадратного уравнения.

(Можно применить:

— теорему, обратную теореме Виета;

— если в квадратном уравнении ах- + вх + с — — , а + в + с О, то

а

— если в квадратном уравнении ах² + вх + с —— О, а — + с = О, то

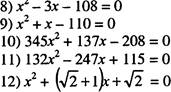
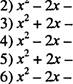                         15 =0            8)х2-зх-

24 = О

24 = О

48 = О 48=0

Ответы:

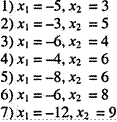
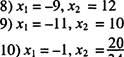208

345

1 15 ll)xt --- l,x2 — 132

12)

2. Разложите квадратный трехчлен на множители: 1)? —6х+9; +6;  15; 4) 2х² +4х— 30; 5) 3х² +6х- 72.

III. Изучение нового материала.

1.                  Рассмотреть некоторые устн ые упр аж н ен и я :

х² —8х+ 15; 2х² +4х— 30; 3х² +6х— 72.

Разложим данные многочлены на множители:

              [х ² - 3х - 5х + 15 = (х² зх) - (5х - 15) =                  - 3) - ях - 3) =

(х —3)(^х —

— Чем являются числа З и 5 для квадратного трехчлена?

2)  2х² + 4х- зо = 2(x² + 2х- 15) = 2(x² - + 5)

        [2(.r² +2х- 15) =                 + 5х- 15) =          - зх) +(5x - 15)) =

— Чему равен первый коэффициент данного многочлена?

— Чем являются числа —5 и З для квадратного трехчлена х² + 2х — — 15 (2х2 + 4х— 30)?

3)  3х² + 6х- 72 = 3(х² + и- 24) = -          + 6)

        [3(х² + 2х - 24) = 3(x² + 6х-4х- 24) =           + 6х) - (4х + 24)) =

— Чему равен первый коэффициент данного многочлена?

— Чем являются числа -6 и 4 для квадратного трехчлена х“ + 2х — -24 (3х² + 6х- 72)?

Получили:

0х² -8х+ = (х-

2) 2х² +4х- зо = + 5); 3) 3х² +6х- 72 = + 6).

2.                  Как разложить на множители квадратный трехчлен ах- + вх + с, если .Xl и — его корни?

З. Доказательство теоремы о корнях квадратного трехчлена.

Теорема:

Если и — корни квадратного трехчлена ах² + вх + с, то ах- +

Да н о : и х2 — корни квадратного трехчлена ах + вх +с. Доказать: ах² + вх -ес = а(х — — И).

Доказательство:

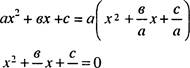
            а     а

По теореме Виета: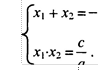

        а                   а

-2 = а(х² —(Х 1 + Х2)Х + Х) •Х2) = а

= а(х — Мх —ИХ + х,Х2) = — XlX) (ХВ — XlX2)) = = а(х(х — М) — Х2(х — Xl)) = а(х — — и).

        Значит, ах² + вх + с = а(х —           х).

4. Рассмотреть примеры 1, 2, З [2, с. 22, 23].

IV. Закрепление изучаемого материала. № 60 (а, в, д, ж, и), 61, 63 (а), 64 (а, б).

Решение:

N2 60 (а, в, д, ж, и).

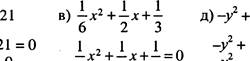а) 3х² - 24х +16y— 15 3х2-24х+21 -y2+ 16y- 15=O х2-8Х+7=о 6 2 З у2- 16Y+ 15=0

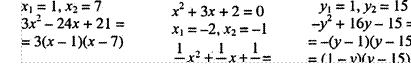
                                               6         2       З

6

7

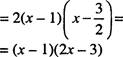
—2х² + 5х + 7 —— —2(х +1) х —— =

2

№ 61.

а) 2х2 — 2х + Д-                             б) —9х2+ 12х—4 - (9х² - 12х+4):

2

= Ч 3х — 2)2;

2х2 — 2х + -2 = О

                        2                    в) ба² + 24а + 9 =

Д = 1 - 1 О

      1                         г) 0,25т² - +4 = (0,5т -2)².

2

2х² — 2х +

2

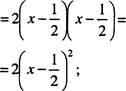
+ 19х-2= + 2)

19х-2=0

д: 361 + 80 = 441 =

--19±21

20

-16 , И

——

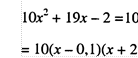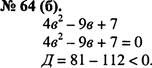
 64 (а, 6).

—3y² + Зу

—3у² + ЗУ + = О

Зу2-Зу- П =О

Д=9+ l32= 141 >O

Квадратный трехчлен —3у² + Зу + имеет два кор-

ня, его можно представить в виде произведения многочленов первой степени.

Квадратный трехчлен

4в- — 93 + 7 не имеет корней, его нельзя представить в ви-

де произведения многочленов первой степени.

V. Итоги урока. Устные упражнения.

1)                     Является ли число 1; 0; —— 1 корнем квадратного трехчлена:

2

а) 2х² — 5х +3; б) х² —— ;

4

2)                     Имеет ли квадратный трехчлен корни, и если имеет, то сколько: а) х² —2х+ 1; б) х² —5; в) х² + 1; г) 3х—х²?

З) Как (по какой формуле) разложить квадратный трехчлен на множители?

Разложите (если это возможно) квадратные трехчлены задания

2 на множители.

Домашнее задание: п. 4, № 62, 63 (б), 64 (в, г), № 167 (а) [2].

Урок 9

Ход урока

1.  Проверка домашней работы.

I . Доказательство теоремы о разложении квадратного трехчлена на множители (у доски).

2.  Решение № 167 (а) (у доски).

З. Вопрос ы по заданиям: № 62, 63 (б), 64 (в, г). Ль 167 (а).

4

4

0,8х² -  —6-25 х+— =

54

—х—5 (4х+1).

55

11. Устные упражнения.

1)   Разложите на множители многочлен:

а) 2х² — 18; б) 4х² +4х+4; в) 4х³ —х²; г) х² — 5х + 6.

                                                х2 —4             2х² -10х

2)   Сократите дробь: а)

Ответ:

1): а) Цх — З)(х + 3); б) нельзя разложить на множители, Д < О;

в) х²(4х— 1); г) (х— З)(х— 2).

2х

Ш. Решение упражнений.

№ 65 (а, в, д), 67 (а), 68, 50 (а, в), 54.

Решение: .N2 65 (а, в, д). а)

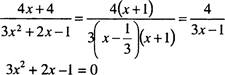3х² +2х-1

Д = 1 +3=4 --1±2

в)

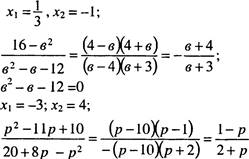p2 —llp+10

д)

20+8р —р

-—p² + 8p + 20 = О

  -20=0 д = 16 + 20=36

Pl = 10,P2 = -2.

№ 67 (а).

36-х2

6—7х+х2

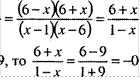Если х = —9, то

6-99 если х= —99, то    = —0,93 ;

+ 99

6+х 6-999 если х = —999, то         = —0,993 . + 999

№ 68:

х² —6х +8

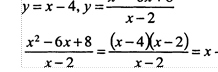
х² — 6х+8 х-2

       Д(у) =        +00)                 

Ответ: областью опредеЈения функции у = х — 4 является про-

х ² —6х+8 межуток (-оо; +0, а областью определения функции у = является промежуток (—с, 2) U (2; +ф), то есть график функции

х² —6х+8

в отличие от графика функции у = х — 4 не проходит

через точку с абсциссой 2.

№ 50 (а, в).

а) х² — 6х+ > 0 при любом значении х. х2-6Х+

При любом значении х (х—

Следовательно, х² — 6х + 10 > 0 при любом значении х;

в) —х² + 20х — 100 0 при любом значении х.

            + 20х-                       - + 100) =               0².        

При любом значении х (х— 10)² 2 О, а Ах— 10)² S О.

Следовательно, —х² + 20х — 10 0 при любом значении х.

.N2 54.

ДАВС, 90⁰ . пусть АВ = х см. Тогда ВС = 6-х см.

2 Ковалева

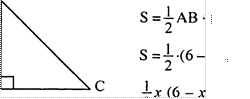²

в                                       = —— х- + 3х = ——(х² — бх) = 2       2          2

- ^L - 2.х.з +9-9) 3)² + 2.

2                                          2                            2                  2

Так как выражение ——(х — З)- при любом х З отрицательно, 2

то сумма — —(х — З) -е— принимает наибольшее значение при х = З.

2

Значит, площадь будет наибольшей, если один из катетов прямоугольного треугольника равен З см. Тогда второй катет также равен З см, то есть треугольник равнобедренный.

IV. Итоги урока.

Домашнее задание: п. 4, № 66, 67 (б), 70 (б), повторить п. 1—3 [2].

Урок 10

Ход урока

1. Проверка домашней работы. Ответы на вопросы учащихся.

П. Организационный момент.

III. Самостоятельная работа.

ВАРИАНТ

№ . Разложите на множители квадратный трехчлен:

а)? -7х+12; 6) 5х² - 5х- Ш; в) 4х² - 144; г) 10х² +29х-3;

д) 63; е) 6х² -4; ж) 17х² -425; з) 5х² + 35. № 2. Сократите дробь:

№ 3*. Упростите выражение:

х³ + х ² —72х

9х-72

40 — 27а

+2a-15

ВАРИАНТ П

№ I . Разложите на множители квадратный трехчлен:

а)? -7х+10; 6) 3х^[1] + 3х-6; в) 7х² -63; г) 5х² + 19х-4;

д)х² +х-72•, е) 7х² +20х-3; ж) 12х² -588; з) 3х² - 12х+3. № 2. Сократите дробь:

№ 3*. Упростите выражение:

Решение:

Вариант 1

а) х2—7х+ 12 = (х— З)(х — 4);

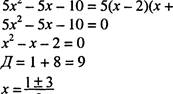6) 5х² -5х- ю =               1);

² -5х- 10 о

2

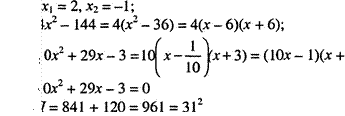в) 4х

-29±31

20

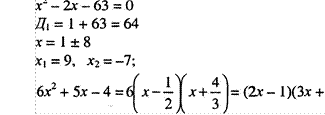
6х2 + 5х — 4 = О д = 25 —48 • 2 =25 +96 = 121

-5±1 1

12

4

                 2'       З

ж) 17х² - 425 = 17(x - 25) = 17(x-

з) 5х² - + 35 = Р -6х+7=0

а ² —4 (а— 2 Ха + 2) _ а —2

            а)                                                  

7a+14

3 ² — в —6

9х -72 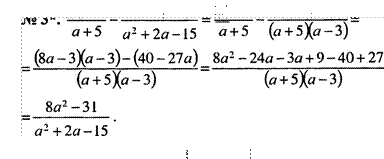а+5

2-7х+

                6) 3х² + -6 = 3(х² + х- 2) =           +

               в) 7х² -63 = 7(x² - 9) = их-          + 3);

³

                  г) 5х                                                                  (5х—

5х² + 19х—4 = О

Д: 361 +80=441 = 212

-19±21

10

5 '

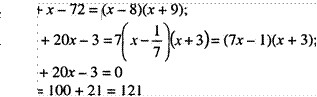7х² +

Д

-10±l l

7

хи — Ъ , Х2= -з.,

ж) l2x² -588 = 12(x2 —

з) 3х² - 12х+3 = 3(х² х- —4х + I = 0

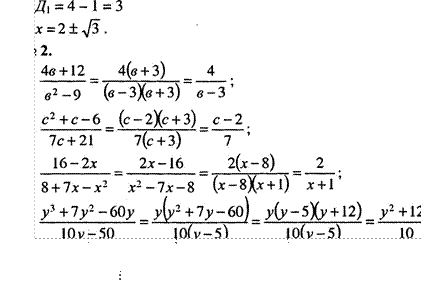9в — 4 44 — I бв в ² + 5в — 14 в +7 — (в +7Хв—2)

(9в — 4 Хв — 2)— (44 —мВ) 93 ² -43+8-44+166

93 ² — +8

в ² + 5в — 14

Можно использовать тес т :

. Определите, имеет ли квадратный трехчлен х- + 4х + 7 корни, и если имеет, то сколько: 1) имеет один корень; 2) не имеет корней;

З) имеет два корня.

2.             Установите, какие из чисел —7; —1; 1; 2; 7 являются корнями квадратного трехчлена х- + 8х + 7: 1) —7; 1; 2) —1; 7; З) —7; —1 ; 4) ни-

какие.

3.             Найдите корни квадратного трехчлена х- — 4х + З:

4.             Разложите на множители квадратный трехчлен 2х- + 4х — 6:

5.             Разложите на множители квадратный трехчлен х — 6х + 8:

1) (х — 4)(х — 2); 2) (х + 4)(х — 2);

х ² —5х+6

6. Сократите дробь

1)

Ответы:

Можно использовать раз ноу ро вне в ы е задан и я :

ВАРИАНТ

. Найдите корни квадратного трехчлена:

а)х² + 6х— 16; б) —х² +2х+ 99; в) 2х² + 7х—4.

Ответ: а) —8; 2; 6)—9; 1 1; в) —4;

2

2. Выделите квадрат двучлена из квадратного трехчлена. За-

кончите решение:

а) р- 18х + 14 18- + 14 =

         6) -х²               + 25 = -(х² + 24х- 25) =          + 2-12.x + 144- 144

-25)

в) — л-2 + 6х 4х2 — Ох) - — —(х² -2.з.Х+9-9)

3.  Разложите на множители квадратный трехчлен:

а) х² —4х— 96; б) 2х² + 8х— 24; в) —х² + 3х + 18.

У к а з а н и е . Воспользуйтесь тождеством + вх + с = а(х — где х, и хэ — корни квадратного трехчлена.

                                     р +2х-15      2х² -5х+2

4.  Сократите дробь: а)

8х — 4

                                                                3х2 +      —4

5.  Найдите значение выражения        при х = —22 6х-2

Ответ: —9.

ВАРИАНТ

1.   Найдите корни квадратного трехчлена:

6) 4х² -20х+25; в) 3х² +Х+4.

Ответ: в) корней нет.

2.   Выделите квадрат двучлена из квадратного трехчлена:

а) х² — 16х+ 100; б) —х² —2х—4; в) 2х² — 8х.

З. Докажите, что при любом значении х: а) .r² — 20х + 140 > О;

б) —х² —6х+ l l < 0.

4.    Из всех прямоугольных треугольников, сумма катетов которых равна 16 см, выделите треугольник с наибольшей площадью.

Ответ: равнобедренный прямоугольный треугольник с катетом 8 см.

5.    Разложите на множители квадратный трехчлен: а) х² — 8х — 9; 6) 3х² + 17х-6; в) 4х² - 12х+9.

5х2-37х+14

6.    Найдите значение выражения        прих= l l . 5х2+3х-2

Ответ:

ВАРИАНТ Ш

. Выделите квадратный двучлен из квадратного трехчлена:

а) х² —4х+ 1; б) —х² + 3х—2; в) 4х² —8х+ З.

2. Докажите неравенство:

а)х² + 12x+44> O•, 6)-х² + 16х-80<0•, в) 4х² - 12х+9 20.

З. Периметр прямоугольника равен 24 см, а одна из его сторон на 2 см больше другой. Меньшую его сторону увеличили на а см, а большую — уменьшим на а см. При каком значении а площадь полученного прямоугольника будет наибольшей?

У к а з а н и е . Найдите сначала длины сторон данного прямоугольника.

4.  Разложите на множители квадратный трехчлен: а) х- + х — 56; 6) -2х- l •, в) 2х² - 108х+ 1458.

2х2+13х-24

5.  Найдите значение выражения при х = ll,25. 2х² -25х+33

Ответ: 77.

Домашнее задание: № 168, 169 [2].

З. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК

Тема (п. 5): ФУНКЦИЯ у = ах²,

ЕЕ ГРАФИК И СВОЙСТВА (2 ч)

Цели: выработать умение строить график функции у — ах и описывать свойства и особенности функции.

Урок 1 1

Ход урока

1. Проверка домашней работы.

Заранее написать решение заданий на доске и выполнить их проверку, корректировку и исправление, если необходимо.

-е

2171 —4

Т- + (уп + 8 = 0

4

ml.2

2m-1

—

5 ±3.

              ml 2 =         

x—l

Ответ: а)

4

11. Анализ самостоятельной работы (теста, разноуровневых заданий).

1.               Итоги работы.

2.               Общий анализ работы.

З. Объяснение задания, с которым не справились большинство учащихся.

111. Изучение нового материала. 1 . Построение графиков функций. На доске изображены графики:

Воп рос ы учащимся:

) Назовите общие свойства функций, графики которых вы видите.

Ответы :

а) область определения — вся числовая прямая;

б) область значений — промежуток [0; +00);

в) убывает на промежутке (—с, 01;

г) возрастает на промежутке [0; +00);

д) график каждой из них проходит через начало координат и симметричен относительно оси Оу.

2) Допустим, что на доске изображены графики функций у = Лх), у = ф), у = р(х) соответственно.

Изобразите графики функций у =Лх) и у = —Лх), у = g(x) и у = —g(x),y = Ах) и у = —q(x). (Учащиеся строят графики в тетрадях, учитель выполняет эту работу на доске.)

З) Назовите общие свойства функций у = —Лх),у = —g(x),

4) Найдите различные свойства функций у =Лх) иу = —f(x).

42

2. Сообщение учителя:

1)      все шесть графиков есть графики функций вида у = ах², а * О;

2)      функция у = ах-, а * 0 является частым случаем квадратичной функции;

З) определение квадратичной функции;

4) график функции у = ах-, а * О называется параболой; определение вершины параболы.

З. Предлагаются во прос ы и задан и я :

1)   Как проще найти а для функции у = ах², если известен ее график? (ОпреДелить по графику значение функции при х = 1 или

2)   Найдите формулы для каждой функции.

(у = х² иу = —х²;у ⁴ х ² иу = —2 х² ; у = 3х² иу = —3х².) 2

З) Как расположен график функции у = ах² относительно оси х, если: а) а> 0; б) а < 0?

4)                    Какая точка является вершиной параболы у = ах², а * О?

5)                    Как построить график функции у = ах² из графика функции у = х², если: а) а> 1; б) 0             1?

6)                    Как построить график функции у = —ах² из графика функцииу = ах², если а > О?

IV. Закрепление изученного материала. № 73, 79 (а, б).

V.    Итоги урока.

Перечислить свойства функции у = ах², если: а) а> 0; б) а < О.

Домашнее задание: п. 5, контрольные вопросы и 2 [2, с. 41]; построить график функции у = х^и, № 74, 79 (в, г) [2].

Урок 12

Ход урока

1. Проверка домашней работы.

Разобрать решение тех заданий, которые вызвали наибольшие затруднения.

П. Опрос учащихся.

1.                    Устный ответ у доски: изобразить график функции у = х² ; дать определение квадратичной функции; перечислить свойства функции у = ах² (а > 0 или а < О).

2.                    Устная ф ронтал ь ная работа с классом.

1)  Какие из графиков следующих функций расположены только

над осью х:

a)y= 2x+ l; г) у = lx l + 1;

д) у = х- — 2; е) у = 2х^[2] + 2? Ответ: г); е).

2)  Найти общее в расположении графиков функций: а) у = х“ + 2; +3; в) у = lx l +x² + l; г)у=—.

х

Ответ: расположены над осью х; не имеют точек пересечения с осью х, симметричны относительно оси у.

З) Как из графика функции у = х² построить график функций:

а)у=—х ² ; у = 2х²; б) у = ?

4) Как построить графики функций: у = —х²; у         ; у = —2х2 2

у = -3х3 у-———х2 9 З

3.               Ответ учащегося, с самоанализом.

Ш. Тренировочные упражнения. № 75, 77, 80 (6, в).

1V. Итоги урока.

1. Построены (заранее на доске) графики функций у = 2х²; у = х-; у (используется таблица).

Ответить на в о п ро с ы :

1)                     Найти значение каждой функции при х = 2; —2; О.

2)                     По графику функции у найти все значения х, при которых 1 5 у 5 4.

З) Сравнить значение функций у у = х в точках х = О;

ВАРИАНТ (ВАРИАНТ 11)

1 . Графику функции у = ах“ принадлежит точка с координатами (—2; З) ((2; —3)). Укажите координаты еще двух точек, принадлежащих этому графику.

2. Проходит ли график функции у = —2х² через точку (—2; —8)

      З. Укажите промежуток возрастания (убывания) функции    

У = -2х².

4.               Существуют ли значения х, при которых функция у = —2х² (у = 2х-) принимает положительные (отрицательные) значения? От-

ветьте «нет» или укажите такие значения.

5.               Постройте график функции у = —2х² (у = 2х²).

Домашнее задание: п. 5, № 76, 78, 80 (а) [2]; изготовить шаблон параболы у = х² и параболы у

Тема (п. 6): ГРАФИКИ ФУНКЦИЙ

Цел и : выработать умение строить графики функции у = ах + п и у = а(х — т)- с помощью параллельных переносов вдоль осей координат.

Урок 13

Ход урока

1. Организационный момент.

Проверка наличия домашней работы; результаты выполнения диктанта.

П. Устные упражнения.

Решение заданий диктанта, выполнение соответствующих

записей на доске.

ВАРИАНТ 1

        1. у =ах²,              3)

а=—,а=— 2 4

х

ВАРИАНТ

²

1. у = ах, (2; —3)

а=——,а=——

            х2                 4

                               -8)     . —2х

-8 = -2,2²

         да.                                  да.

             . — —2х²,         

Нет.(О; +00)

      5. у = —2х2                             ⁵ . у- ^2х2

                                                                               о           2

Ш. Изучение нового материала.

На доске изображены графики функции (см. рис. а, б, с. 47).

1. Во про с ы учащимся:

1)    Рис. а. Найдите значения функций у         иу        + 1 , если

значения аргумента равны ±2; 0 (составляются соответствующие таблицы).

      — Как связаны значения функции у              +1 и значения функ-

ции у           при одних и тех же значениях аргумента?

       — Как из графика функции у              получить график функции

2)    Рис. б. Найдтр значения аргумента функций у = 3х^[3] иу = З(х — l)², если значения функции равны 0; 1; З (составляются соответствующие таблицы).

— Как связаны аргументы функции у = З(х — и аргументы функции у = 3х² при одних и тех же значениях функции?

— Как из графика функции у = 3х² получить график функции

— Как из графика функции у = ах- можно получить график функции у = ах- + п, у = а(х — у = а(х — + п?

IV. Тренировочные упражнения.

№ 87 (а, г), 88; № 90 — самостоятельное решение с последующей проверкой и обоснованием решения.

V.    Повторение.

№ 98 (б) — са мо стоят ел ь ное решение в тетрадях, один ученик выполняет его на откидной доске, затем открывает доску и объясняет решение.

VI. Итоги урока.

Устное решение с комментариями № 95.

Домашнее задание: п. 6, № 87 (б, в), 89, 98 (а), 99 (а, б) [2].

Урок 1 4

Ход урока

1. Проверка домашней работы.

1.     Учащиеся выполняют № 87 (б), 87 (в), 89 у доски с последующим обоснованием и формулировкой соответствующих выводов.

2.     Самостоятельное решение № 99 (в, г), 98 (а) в тетрадях, проверка выполнения заданий (на откидной доске заранее приготовлены решения).

 99 (в, г).

в) 2х + 4,2         г) 3х - > 5,5х 4х-20    5,5х- 3х < 2х2-           2,5х <

№ 98 (а).

о,6а - (а + = 0,27 0,6а — а- — 0,6а —0,09 = 0,27 -а² = 0,36 а² = —0,36 Нет решения.

Ответ: нет решения. З. Устные ответы учащихся.

П. Тренировочные упражнения.

№ 91, 93 — ученики сам ос тоя тел ь но выполняют решения в тетрадях; на доске заранее изображены системы координат; ученик, первый выполнивший одно задание, выполняет его на доске и комментирует свое решение и т. д.

№ 96, 97 — решение у доски, с объяснением.

Ш. Итоги урока.

1.                Самостоятел ь ная работа (по вариантам):

ВАРИАНТ

В одной и той же системе координат постройте графики функ-

ций:у=——-r ² ; у 2) ² — 0,5.

2

ВАРИАНТ П

В одной и той же системе координат постройте графики функЦИЙ:У= 2х²; у=—2(х+ l)² ; +1,5; у=2(х—2)

2.                Собрать работы учащихся на проверку.

3.                Разобрать решение самостоятельной работы.

4.                Самоанализ. (В каких заданиях допущены ошибки? Почему? Формулировка соответствующих положений теории.)

Домашнее задание: п. 6, контрольные вопросы [2, с. 41], № 92, 94; из сборника № 857, 859, 867 [4, с. 175, 176].

тема (п. 7): ПОСТРОЕНИЕ ГРАФИКА

КВАДРАТИЧНОЙ ФУНКЩШ (3 ч)

Цели: выработать умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы; выработать умение строить график квадратичной функции; довести до поНИМаНИЯ учащихся, что график функции у = ах² + вх + с может быть получен из графика функции у = ах- с помощью двух параллельных переносов вдоль осей координат.

Урок 1 5

Ход урока

1. Проверка домашней работы.

1.                     Во п рос ы учащихся по заданиям № 92, 94.

2.                     Заранее написать решения № 857, 859, 867 (из сборника), устно разобрать каждое решение (объяснения учащихся).

        ЛЕ 857.                         859.                            ЛЕ 867.

З. Устные вопрос ы :

№ 857.

— При каких значениях х функция принимает положительные значения?

— Укажите промежуток, в котором функция возрастает (убывает). — Чему равно наибольшее значение функции?

.N2 859.

— Укажите значения х, при которых у < 0.

— Укажите координаты вершины параболы.

     — Чему равно наименьшее значение функции?         

— Как из графика функции у = —х² построить график функции

                                                       50         

П. Изучение нового материала. Объяснение учителя.

1.    Поставить перед учениками задачу — построить график квадратичной функции у = ах- + вх + с, выяснить, что он собой представляет. Нужно воспользоваться умением строить график функции у = а(х — + п из графика функции у = ах² с помощью параллельных переносов вдоль осей координат.

2.    Поэтому выделим из трехчлена ах² + вх + с квадрат двучлена.

ах + вх+с= а х² +—х+—

+

Тогда т = —— 2а           4а

Следовательно, функция у = а.х² + вх + с является квадратичной, график — парабола, которую можно получить с помощью двух па-

раллельных переносов: вдоль оси х на             влево и вдоль оси у на

в ² - 4ас вниз.

Точка (т; п) — вершина параболы, прямая х = т — ось симметрии. При а > О (а < О) ветви параболы направлены вверх (вниз).

З. Разработка алгоритма построения графика квадратичной функции (записать его на доске).

Алгорипи построения графика кваДрапшчной функции

1)                     Найти коорДинаты вершины параболы (т; п), где т = —— 2а и отметить ее в коорДинатной плоскости.

2)                     ОпреДелить направление ветвей параболы.

З) Составить уравнение оси симметрии х = т и изобразить ее в коорДинапшой плоскости.

4) Построить несколько точек, принадлежащих параболе (точки пересечения с осями координат). 5) СоеДинить отмеченные точки.

4. Рассмотреть пр и ме р ы 1, 2, З [2, с. 37—39], оформить решение одного примера на доске и в тетради.

Ш. Закрепление изученного материала. № lOl, 102 — решение у доски с объяснением.

IV. Итоги урока.

Повторить схему построения графика функции у = ах² + вх + с и записать ее в тетрадь.

Домашнее задание: п. 7, № 103, 109, контрольные вопросы [2,

с. 41].

Урок 16

Ход урока

1. Организационный момент.

Воп рос ы учащихся по домашней работе, выборочная проверка домашней работы.

П. Устные упражнения.

1.     Определите координаты точки пересечения параболы с осью ординат: а) у = 3х² — 8х + 9; б) у = —х² + 5; в) у = 3х — 2х². Ответ: а) (0; 9); б) (О; 5); в) (О; О).

2.     Найдите координаты точек пересечения параболы у = .х² — 36 с осями координат.

Ответ: (0; —36) — точка пересечения с осью у,

(6; 0); (—6; 0) — точки пересечения с осью х.

З. Укажите координаты вершины параболы, направление ветвей, уравнение оси симметрии:

а) у = х² — 1; б) у = —2х² + 5; в) у = (х — 2)² ; г) у = —3(х + —4.

52

Ответ: а) (0; —1 ); ветви направлены вверх; х = О;

б) (0; 5); ветви направлены вниз; х = О;

в) (2; 0); ветви направлены вверх; х = 2;

г) (—1 ; —4); ветви направлены вниз; х = —1.

Ш. Тренировочные упражнения. № 104 (а, б), 105.

№ 104 (а, б) — решение у доски с объяснением,

№ 105 (а, б) — самостоятельное решение в тетрадях, одновременно двое учеников решают на откидной доске или «за доской», проверка решения.

№ 105 (в) — самостоятельное решение, проверка правильности построения графика по заранее приготовленному рисунку.

Обратить внимание учащихся на построение графика: а) по алгоритму; б) с помощью параллельных переносов (№ 105 а, в). Построить графики функций у 1 + 5 и у = —х² + 6х — 9 с помо2

щью шаблонов у          и у = х-.

IV. Самостоятельная работа.

ВАРИАНТ

№ 1 . Найдите координаты вершины параболы:

a)f(x) = х² —6х + 4; 6)f(x) = —х² —4х+ 1; в)Лх) = 3х² — 12х + 2.

№ 2. Постройте график функции у = х² — 6х + 4. Найдите по графику: а) нули функции; промежутки, в которых у < О, у > О; б) промежутки убывания и возрастания функции, наименьшее ее значение.

ВАРИАНТ П

№ 1. Найдите координаты вершины параболы:

a)f(x) = Р +4х+2; 6)f(x) = —? +6х+3; в)Лх) = 4х² —8х— 1.

№ 2. Постройте график функции у = х² + 4х + 2. Найдите по графику: а) нули функции; промежутки, в которых у < О, у > 0; б) промежутки убывания и возрастания функции, наименьшее ее значение.

Решение:

                     Вариант                                        Вариант

   а)Лх) = х2 —6х + 4.                      а)Лх) = х² + 4х + 2.

(т; п) координаты вершины (т; п) — координаты вершины параболы.        параболы.

2а

П = 3 ² — +4=9— —5 (З; —5) — координаты вершины параболы;

6)f(x) = —х

+ 4-2 + = —4+9=5

в)Лх) = 3х²

2а п - 3-2² - 12-2 = 12-24+ 2=-10 (2; -10).

у = х- — 6х + 4 — квадратичная функция, график парабола, ветви которой направлены вверх, так как а = I > О; (З; —5) — координаты вершины параболы. Прямая х = З — ось симметрии.

х

(—2; —2) — координаты вершины параболы;

                          — —х- — 6х + З

2а п = —(—3)² + 6-3 +3 =

= —9+ 18+ 3 =2

в) f(x) = 4х2-8х- 1

2а

+ 4х + 2 — квадратичная функция, график — парабола, ветви которой направлены вверх, так как а = > 0; (—2; —2) — координаты вершины параболы. Прямая х = I — ось симметрии.

а) 0,8 и 5,2 — нули функции, у при 0,8 < 5,2,

0 при х < 0,8, х > 5,2;

б) функция убывает на промежутке (—оо; З], возрастает на промежутке [З; —5 — наименьшее значение функции.

а) —3,4 и —0,5 — нули функции, у < 0 при —3,4 < х < —0,5, у> 0 при х < —3,4, х > —0,5;

б) функция убывает на промежутке (—с, —2], возрастает на промежутке [—2; —2 — наименьшее значение функции.

Домашнее задание: контрольные вопросы [2, с. 41], № 106; из сборника № 877, 880, 881, 894 [4, с. 176-178].

Урок 17

Ход урока

1. Организационный момент.

II. Анализ самостоятельной работы.

Необходимые записи на доске приготовить заранее.

1.   Итоги работы.

2.   Разбор типичных ошибок.

3.   Выполнение работы над ошибками.

III. Устные упражнения. 1. Разложите на множители:

а) х² —4; б) 7х— 14х²; в) 258— lOa+ 1; г) с² —7с + с.

       Ответ: а) (х—        + 2); б) 7x(l — 2-х); в) (5а— l)²; г) с(с — 6).

2. Укажите координаты вершины параболы, направление ее ветвей, уравнение оси симметрии, координаты точки пересечения с осью у.

    а) у = —3х² — 5;              +2х+ 1.

Ответ: а) (0; —5); ветви параболы направлены вниз, х = О — ось симметрии; (0; —5); б) (—1; 0); ветви параболы направлены вверх, х = —1 — ось симметрии; (0; 1).

1V. Тренировочные упражнения.

       № 165       167 (6, в), 168 (а, 6), 183 (а, в, д).

V. Итоги урока.

Контрольные вопросы [2, с. 4 1, 25].

Домашнее задание: подготовиться к контрольной работе:

 1-3, № 165 (6), 167 (а, г), № 183 (6, г, е)

Урок 1 8

КОНТРОЛЬНАЯ РАБОТА № 1

ВАРИАНТ

1 . Разложите на множители квадратный трехчлен:

а) Р- 14х+45; 6) Зу² +7 -6.

2. Постройте график функции у = х² — 2х — 8. Найдите с помоилью графика:

а) значения у при х = —1,5;

б) значения х, при которых у = З;

в) нули функции; промежутки, в которыху> 0 и в которых у < О;

г) промежуток, в котором функция возрастает.

Зр2+р—2

З. Сократите дробь

4—9р2

4.                     Найдите наименьшее значение квадратного трехчлена

5.                     Не выполняя построения, определите, пересекаются ли парабола у = —х² и прямая у = 6х— 15. Если точки пересечения существуют, то найдите их координаты.

ВАРИАНТ П

1 . Разложите на множители квадратный трехчлен:

а)  6) 5у² + 9у-2.

2. Постройте график функции у = х² — 4х — 5. Найдите с помощью графика:

а) значения у при х = 0,5;

б) значения х, при которых у = З;

в) нули функции; промежутки, в которыху> 0 и в которых у < О;

г) промежуток, в котором функция убывает.

З. Сократите дробь l—16c2

4.   Найдите наименьшее значение квадратного трехчлена

5.   Не выполняя построения, определите, пересекаются ли парабола у = —х ² и прямая у = 12 — х. Если точки пересечения сущест-

2

вуют, то найдите их координаты.

ВАРИАНТ Ш

. Разложите на множители квадратный трехчлен:

           а)       12х + 35; 6) 7у² + 19y-6.

2. Постройте график функции у = х² — 6х + 5. Найдите с помоилью графика:

а) значения у при х = 0,5;

б) значения х, при которых у = —1;

в) нули функции; промежутки, в которыху> 0 и в которых у < 0;

г) промежуток, в котором функция возрастает.

5а2 +19a —4 З. Сократите дробь l-25a2

4.    Найдите наименьшее значение квадратного трехчлена х“ — 8х + 7.

5.    Не выполняя построения, определите, пересекаются ли пара-

бола у = —х² и прямая у = 5х— l6. Если точки пересечения сущест4 вуют, то найдите их координаты.

ВАРИАНТ IV

I . Разложите на множители квадратный трехчлен:

а) е- 18х + 45; 6) 9х² + 25х- 6.

2. Постройте график функции у = х² — 8х + 13. Найдите с помощью графика:

а) значение у при х = 1,5;

б) значения х, при которых у = 2;

в) нули функции; промежутки, в которых у > 0 и в которых у < 0;

г) промежуток, в котором функция возрастает.

7B2+llB-6

З. Сократите дробь

9 — 496 ²

4.    Найдите наименьшее значение квадратного трехчлена —х- + 6х — 4.

5.    Не выполняя построения, определите, пересекаются ли пара-

бола у= —х ² и прямая у = 20 — 3х. Если точки пересечения сущест5 вуют, то найдите их координаты.

Решение:

Вариант 1

1.

а) х² — + 45 = (х — 5)(х 9).

          х² —       + 45

Ц = 49 — 45 = 4

4

зу2 + 7», — 6 = О

6

2. у = х² — 2х — 8 — квадратичная функция, график — парабола, ветви которой направлены вверх, так как а = > О.

        Точка (т; п) — вершина параболы, т = ——           - l n - l

= —9. Точка (1; —9) — вершина параболы.

Прямая х = — ось симметрии.

6) х = -2,6; 4,4;х

в) —2 и 4 — нули функции, О при —2, х > 4, то есть хе (4; +ф)., у < 0 при —2 < 4, то есть хе (—2; 4);

г) [1; +00).

Зр ² + р— 2 З.

4—9р2 зр² +р-2=О д: + 24 = 25

—l±5

6

_2

З

4. х² —6х+ ll.

у = х² — 6х + — квадратичная функция, график — парабола, ветви которой направлены вверх.

Наименьшее значение квадратного трехчлена х — 6х + 1 1 — это ордината вершины параболы у = х² — 6х + 1 1

2 — наименьшее значение данного квадратного трехчлена.

5.  15.

15 З

2-6х+ 15=0

Ц = 9— 5 = 4 > 0; два корня. 4

       Точки пересечения параболы у              и прямой у = 6х — 15 су-

ществуют:          

= 15, » = з;

152

75, п

       (15; 75) и (3; 3)-точки пересечения параболы у              и прямой

y=6x- 15.

Вариант

1.

               7).

4

6) 5у² +9у-2=5        (5у— 5у2+9у-2=О

Д: 81 +40= 121

У 1.2 =

5

2. у = х- — 4х — 5 — квадратичная функция, график — парабола, ветви которой направлены вверх, так как а = I > О.

Точка (т; п) — вершина параболы, т =——, т = 2, п = 2² —42 5 2а

4 8 5 =—9. Точка (2; —9) — вершина параболы.

     Прямая х = 2 — ось симметрии.                                 у= * —4х—5

5,3;

в) —1 и 5 — нули функции,

х

у > 0, если хе (5; +00) у < 0, если хе 5);

             48 +7с—2              4

з.

                     1— 16c ²                 (1                 + 4с)

        48 + 7с — 2 = О

—7±9

CI,2 =

8

Наибольшее значение квадратного трехчлена —х² + 4х + З — это ордината вершины параболы у = —х- + 4х + З, ветви которой на-

правлены вниз т = -- —-

7 — наибольшее значение данного квадратного трехчлена

, у = 12 — х.

--х ² = l2—x 2

—х ² +х— 12=0

2 х² +   24 = о

+ 24 = 25 > 0, два корня.

4

Парабола у прямая у = 12 х пересекаются в двух точ-

ках:

Xl,2

= 4, Х2 = —6 ;

= ^L .16 = = 18.

                  2                     2

(4; 8) и (—6; 18) прямой

y= 12 х

Вариант III 1.

Р - 12х+35 =0

4

6) 7у

7у2 + 19y — 6 = О

д: + 168 = 529

-19±23

Yl,2 =

2

Yl

7

2. у = х2 — 6х + 5 — квадратичная функция, график — парабола, ветви которой направлены вверх, так как а = > 0.

Точка (т; п) — вершина параболы, т , — 32 —            + 2а

+5 = 9— 18 + 5 = —4. Точка (З; —4) — вершина параболы.

Прямая х = З — ось симметрии.

а) у = 2,5;

6) х- l,l; 4,9;

в) 1 и 5 — нули функции, у> 0, если хе (5; +0); у < О, если xE(l; 5);

З.

58 + 19a-4=O д: 361 + = 441 = 21 ²

-19±21

3'

Наименьшее значение квадратного трехчлена х² — 8х + 7 — это ордината вершины параболы у = х- — 8х + 7, ветви которой направлены вверх.

          в   4, п = 4² — 8-4 +  7 —9.

2а

—9 — наименьшее значение данного квадратного трехчлена

у = 5х— 16.

--х ² = 5х— 16

4

4 х- - 20х + 64 = о

= 100 — 64 = 36 > 0, два корня.

4

       Парабола у          и прямая у = 5х — 16 пересекаются в двух точ-

ках:

Xl.2= lO±6

= 16, Х2 ——4

у =L.16² —— 64, =—. 42 = 4.

44

       (16; 64) и (4,• 4)                                                                      и прямой

у: 5х— 16.

Вариант IV 1.

4

= 15, х— з;

⁰

6) 9х- + 25х-6=

9х² + 25х-6=0 д- 625 + 216 = 841 = 29²

-25±29

18

9

2. у = х- — 8х + 13 — квадратичная функция, график — парабола, ветви которой направлены вверх, так как а = I > О.

         Точка (т; п) — вершина параболы, т —в ,                     , _ 2 8-4+ 13 =

= —3. Точка (4; —3) — вершина параболы.

Прямая х = 4 —ось симметрии.

y=x² -8.r+ В

а) у 3,4;

6)xz 1,7; 6,3;

в) 2,3 и 5,7 — нули функции, у > О, если хе (—с, 2,3)U (5,7; +00) у < 0, если хе (2,3; 5,7);

          г)        +00).

з.

7в2+ Пв-6=О д: + 168

-1 1±17

Bl,2 =

14

³ , 32=-2.

7

Наибольшее значение квадратного трехчлена —х + 6х — 4 — это ордината вершины параболы у = —х² + 6х — 4, ветви которой на-

правлены вниз, т+ 18-4= 5.

5 — наибольшее значение данного квадратного трехчлена —х2 + 6х — 4.

       5. у         , у = 20 — 3х.

20-3х

5

—2+3х-20=0

5

 + 15хд= 225 + =625 > 0, два корня.

Парабола у = —х² и прямая у = 20 — 3х пересекаются в двух точ-

ках:

-15±25

Xl,2 =

2

       =L.25 = 5,У2        • 400 = 80.

              5                     5

      (5; 5) и (—20; 80)                                                                      и пря-

мой у = 20 — 3х.

З Ковалева

Ответы:

        Вариант 1. 1: а) (х -       - 9): 6) (Зу-            + 3). 2: а) -3; 6) -2,6 и

4,4; в) —2 и 4; 0 при .rG    —2)U(4; +3-*)•, < 0 при хе     4) p+l

г)      +00). З.                   4. 2. 5. 05; 75) и (З: 3).

Зр + 2

Вариант П. 1 : а) (х — 3)(.r — 7); б) (5у — l)O, + 2). 2: а) —6; б) —1 ,5 и 5.3; в) —l и 0 при +3?): < О при 5)

4. 7. 5. (4; 8) и (—6: l 8).

Вариант 111. 1 : а) (х — — 7): б) — 3). 2: а) 2.5: 6) и 4,9; в) I и 5; v > 0 при +7): < 0 при xG(l; 5)

(1 -4- 4

4. —9. 5. (16; 64) и (4: 4).

5a+l

Вариант 1V. 1 : а) (х

б) 1,7 и 6,3; в) 2,3 и 5.7; у > 0 при

5,7), г) [4; +0). 3.

76, +3

 4. НЕРАВЕНСТВО С ОДНОЙ ПЕРЕМЕННОЙ

Тема (п. 8): РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ

С ОДНОЙ ПЕРЕМЕННОЙ (3 ч)

Цел : сформировать умения решать неравенства ах- + вх + с > 0, ах- + вх + с < 0, где а 0, с опорой на сведения о графике квадратичной функции (направление ветвей параболы, ее расположение относительно оси Ох).

У ро к 1 9

Ход урока

1. Анализ контрольной работы.

I . Общий анализ контрольной работы.

2. Объяснение заданиЙ. с которыми не справились большинство учащихся.

З. Демонстрация лучших работ.

П. Актуализация знаний.

Решить устно:

1.    Что можно сказать о количестве корней уравнения + вх + с = 0 и знаке коэффициента а, если график квадратичной функции у = ах + + вх + с расположен следующим образом:

'L. (fv nf

2.    Назовите промежутки знакопостоянства функции у + вх + с, если ее график расположен указанным способом:

а)в)

 х

хх

Ответ:

1.    Рис. а: два корня, а > 0; рис. б: нет корней, а < 0; рис. в: нет корней, а > О; рис. г: один корень, а < 0.

2.    Рис. а: у> 0 при х е (М; и); у < 0 при хе(--оо; (И, +00); рис. б: у > О при хе рис. в: у> О при хе (—оо; хо) U (хо; +00).

111. Изучение нового материала.

1.                     Объяс нен ие решения примеров 1—4 из п. 8 [2, с. 41—43].

2.                     Состамение алгоритма решения неравенств вида + вх + с > О, ах² + вх + с < О, а 0.

IV. Закрепление изученного материала. № (а-г), 1 15 (а, в).

Самостоятельное решение; ученик, первый выполнивший задание (решивший одно неравенство), записывает его реШеНИе на доске и комментирует V. Повторение.

№ 129 (а) — решение у доски, с объяснением.

IV. Итоги урока.

Повторение алгоритма решения неравенств второй степени с одной переменной.

Домашнее задание: п. 8, № 16, 128, 129 (б) [2].

Урок 20

Ход урока

1.                      Проверка домашней работы. П. Устные упражнения.

На рисунках изображен график функции у = ах- + вх + с.

. Определите знаки коэффициентов а и с и дискриминанта Д.

2.                      Назовите значения переменной х, при которых данная функция: а) принимает значения, равные нулю. больше нуля, меньше нуля; б) возрастает, убывает; в) принимает наибольшее значение,

наименьшее значение.

3.                      Решите неравенство: а) ах- + вх + с > 0; б) ах- + вх + с О.

а)в)                                                                               г)

Ответы .

1.             Рис. а: а > 0, с > О,Д> О, рис. б: а > О, с > О, Д = О; рис. в: а < О, с < О, Д < О; рис. г: а<О, с =           О.

2.             Рис. а: а) х = 1; з;      1, х > З;          З; 6) [2;

в) при х = 2 функция принимает наименьшее значение.

Рис. б: а) х = —2, (—с, —2)U (—2; +O•, б) [—2; +00), (—с, —2]; в) при х = —2 функция принимает наименьшее значение.

Рис. в: а) у О, (—с, +0); б) 4]; [4; +1))•, в) при х = 4 функция принимает наибольшее значение.

     рис. г: а) х —4; О., 0); (—оо; —4)U (0; +o)•, б) (—с, —2], [—2; +0);

в) при х —2 функция принимает наибольшее значение. З. Рис. а: а)  +00); 6) (1; 3).

        Рис. б: а) (—с, —2)U (—2;      б) нет решений.

Рис. в: а) нет решений; б) (—с, +00).

Рис. г: а) (—4; 0); б) (—оо., —4)U +00).

111. Тренировочные упражнения. (д, е, ж), 1 17, 1 18.

IV. Итоги урока.

Математический д и к та н т .

ВАРИАНТ (ВАРИАНТ П)

1.                     Корнями квадратичной функции у = —3х² + 6х + 9 (у = —2х² +

+ 2х + 12) являются числа 3 и —1 (—2 и З).

Укажите промежуток возрастания функции.

2.                     Корнями квадратичной функции у = —3х² + 6х + 9 (у = —2х + + 2х+ 12) являются числа 3 и —1 (—2 и З).

Укажите множество решений неравенства

—3х2 + 6х + 9 О (—2х2 + 2х+ 12 > О)

З. Наибольшее или наименьшее значение принимает функция у -3х² + 6х+ 9 О = -5х² + 3)?

4.     Найдите промежуток возрастания функции у = 2х² — 4х —6 (у = 3х² — 6х — 9).

5.     Решите неравенство 2х² —4х — 6 > О (3х² — 6х —9 < О).

Взять на проверку тетради учащихся. Проверить решение заданий математического диктанта, провести самоанализ. (Какие задания вызвали наибольшее затруднение?)

Ответ ы :

                    Вариант                                         Вариант

2.  4-00)

З. Наибольшее значение

Домашнее задание: п. 8, контрольный вопрос [2, с. 50], № 1 15

(6), 19, 129 (в, г).

Урок 2 1

Ход урока

1. Организационный момент.

1.                     Вопросы учащихся по домашней работе.

2.                     Цели и задачи урока (закрепление навыков решения неравенств второй степени с одной переменной), сообщение хода урока.

II. Тренировочные упражнения.

Самостоятел ь ная работа с последующими проверкой и самооценкой.

Учащимся предлагаются задания по вариантам.

     ВАРИАНТ 1. 1. № 189     2. № 123       З. 120        4. № 122

5. №191 (6).

ВАРИАНТ II(IV). 1. № 189 (б). 2. № 123 (б). З. 121 (б).

4. № 191(a). 5.№191 (6).

    ВАРИАНТ Ш. 1. № 189 (в). 2. № 123     З. 120        4. № 122

5.№191 (6).

Оценка выставляется по числу правильно решенных заданий. Ученик имеет право получить консультацию учителя по вопросам, касающимся заданий. Пятое задание лишено консультаций. За одну консультацию снимается 0,25 балла. Вопрос ученика — это поднятая рука. Чтобы не забыть о количестве консультаций, учитель на полях тетрадей делает отметку «к».

После выполнения работы ученики сами проверяют полученные результаты по контрольным карточкам или по записям, выполненным заранее на доске учителем.

Учащиеся сами оценивают результаты выполнения самостоятельной работы, выставляют себе оценку и сообщают ее учителю.

Контрольные карточки

ВАРИАНТ (Ш)

1.                      № 189 (а)        189 (в»

а) .r² - 5х - 50 < О.

у = х- — 5х — 50 — квадратичная функция, график — парабола, ветви которой направлены вверх:

-50=0 д = 25 + 200 = 22.5

5 15

Xl,2 =

2

—5 и 10 — нули функции

У = х- - 5х - 50

в) Зу2 + 4у —4 > 0.

у = 3х- + 4х — 4 — квадратичная функция, график парабола, ветви которой направлены вверх:

х

2.                      № 123 (а). 7х ² - lO.r+ 7 >O у = 7х² — lOx + 7 — квадратичная функция, график — парабола, ветви которой направлены вверх.

7х-- 10х+7 =0

Ц = 25 — 49 < О

4

Парабола у = 7х² — lOx + 7 не пересекает ось Ох, значит, неравенство верно при любом значении х.

з. № 120

2х² + 8х- lll < + 6) 2х² lll <6х² ЗО 4х² + 81 >О.

При любом значении х 4х² 0, следовательно, 4х² + 81 > О. Значит, х Е +00). Ответ: (—с, +00).

4.  № 122 (а).

У = 12х—3х2

3х² 2 о 3х2у = 3х² — 12x — квадратичная функция, график — парабола, ветви которой направлены вверх:

3х² - 12x=O

3х(х — 4) = О

точки пересечения параболы у = 3х² — 12х с осью Ох.х

Ответ:Д(у)

5.  № 191 (6).

у = 9х² — 24х + 16 — квадратичная функция, график — парабола, ветви которой направлены вверх.

9х² - их + 16=0

Ц = 144 — 144 = о

4

 0 — верно при любом значении х, кроме Д.

Ответ: ДО) — — — ⁰⁰ ;

ВАРИАНТ 11(W)

1.  № 189 (6).

—т- — 8m + 9 Ох2 + 8х — 9 пр + 8т — 9 S О

 + 8m —9 = О х при т = —9 и 1.

у = х² + 8х — 9 — квадратичная функция, график — парабола, ветви которой направлены вверх, (—9; 0), (1; О) — точки пересечения параболы с осью Ох.

Ответ: [—9; 1].

2.  № 123 (6).

—6у² + lly— 6y² - lly+ lO>O у = 6х² — llx + 10 — квадратичная функция, график — парабола, ветви которой направлены вверх.

Д: 121 -240<0.

Парабола у = 6х² — llx + 10 не пересекает ось Ох, значит, неравенство бу^р — ly + 10 > 0, а следовательно, и неравенство —6у² + + lly— 10 верно.

З. № 121 (6).

          (5х +           - 2) < 21х² - пх- в

пх- в

(4х — > 0 — верно при любом значении х, кроме —

144 —9х² > о

2— 144 «о

9х² — 144 — квадратичная функция, график — парабола, ветви

которой направлены вверх:

          9х2 — 144 = 0           

9х- — 144

144

9

(±4•, 0) — точки пересечения параболы с осью Ох х е (—4; 4). Ответ: ДО) = 4).

       5.    191 (б) (см. вариант I (lll)).

III.  Решение.

№ l80 (г, д, е) — у доски, с объяснением.

IV. Итог урока.

Анализ урока.

—Чему научились на уроке? Что нового узнали на уроке?

Домашнее задание: п. 123 (в. г), № 124, l27 [2].

Тема (п. 9): РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ (3 ч)

Цел и: выработать умение решать рациональные неравенства методом интервалов.

Урок 22

Ход урока

1. Организационпьш момент.

11. Актуализация знаний.

1 . Индивидуальные (разноуровневые) з ад а н и я

             КАРТОЧКА                           КАРТОЧКА 2                       КАРТОЧКА З

1.   Найдите множество Найдите множество 1. I ]айдите множество решений неравенства: решений неравенства: решений неравенства:

а) .r² 49; 6)        10.r•,

в) 3х² + 6 7.r.                                                                                   в) 1-6х 3х²

Окончание табл.

2.   Устные упражнения:

1)  Разложите на множители выражение:

а) х² — 144; б) 7 —у²; в) а^з + 2а² + а; г) + 1; д) 3² — lOB + 9.

Ответ:

12); 6) (ф-у№+у); в) аф+ l)² •,

       г) (т +          — т + 1); д) (в— 9)(в — 1).

2)  Являются ли числа 0;           ; —3 решением неравенства:

а) 2х+3 < 0•, 6)X² S O•,

Ответ: а) решение неравенства —3; б) решение неравенства 0;

в) решение неравенства —3.

З) При каких значениях х имеет смысл выражение:

а)

             2х-1        х2 + З

Ответ: а) х — любое, кроме -— • б) х — любое; в) х —1; г) х S О.

2 '

4) Решите неравенство: а) х

в) а- + 2а+ I > 0; г) в

Ответ: а) (-с, —12]U [12; +ф); б) в) а —любое, кроме —1; г) (1; 9).

З. Ответ на контрольный вопрос №  на с. 50. Ш. Изучение нового материала.

1.   Объяснение уч ителя .

Рассмотрим функциюЛх) = (х — — .x2) (х — хп), где х — переменная, числа .rl, .r2 — нули функции. Область определения функции разбивается нулями на промежутки, в каждом из которых функция сохраняет свой знак, а при переходе через нули ее знак меняется.

Это свойство используется для решения неравенств

      . (х —хп) > 0, (х           — ... (х — хп) < 0.

2.   Рассмотреть при мер ы 1—4 [2, с. 47—49].

lV. Тренировочные упражнения. № 131, 133, 134.

V.     Повторение.

№ 142. Самостоятел ьное реше н ие ; ученик, первый выполнивший задание, записывает решение на доске.

VI.  Итог урока.

Рассказать, как решают неравенства методом интервалов.

Домашнее задание: п. 9, контрольные вопросы [2, с. 50], № 132, 135, 143.

Урок 23

Ход урока

1.  Проверка домашней работы.

Устно проверить ответы, разобрать возникшие вопросы.

11. Решение.

№ 136, 138, 140.

Устно разобрать методы решения каждого номера. С ам остоя тел ьное решен ие учащихся. Одновременно один ученик выполняет номер на откидной доске и затем комментирует решение.

111. Итог урока.

1 . Ответы учащихся на контрольные вопросы [2, с. 50].

2.  Самостоятельная работа.

ВАРИАНТ       ВАРИАНТ П 1 . Решить неравенство методом интервалов:

в) (х — 4)(х + 8) > 0;

г) (х — 4)(х + 4)(х + 2) < 0;

д) (х + 16)(x + 20)(х — 30) > О,

е) (х— 2)(х + ll)(x + 8) < О.

2. Найти область определения функции:

      Ответы:                                 Ответы :

д) (-20; -16)U (30; +0;

2: а) ДО) = —9] U [2; +0); 6) Ду) = [0; [ В; +о.

Домашнее задание: п. 9, № 137, 139, 141 [2].

Урок 24

Ход урока

И. Анализ самостоятельной работы. П. Проверка домашней работы. Ответить на вопросы учащихся.

111. Устные упражнения. . Решить неравенство:

² -2z +l SO•,

4

г) х² + Шх + 25

Ответ: а)

            г)            —5)U            +00); д) [—1; 15].

IV. Тренировочные упражнения.

№ 195 (а, 6, г), 198 (а, г), 199 (6, в), 200 Решение у доски, с объяснением. V. Самостоятельная работа.

                              ВАРИАНТ                                                     ВАРИАНТ 11

1 . Решить неравенство:

а) х(х + 8)(х — 17) S О;

- 20) > О,

2. Найти множество решений неравенства:

—(х — l)(5 — х)(х + 20) > О             -(х -         -         + 10)

З. Решить неравенство:

        х-з            2х-10                   х—4          3х-72

4. Найти область определения функции:

Решение:

Вариант

            1. а) +            - 17) О;

                                                 [—5; —llU +00)

[0; 2,5)

BapuaHT II

        (-w -l          [0; 15]                            

                      (-10;         (9;

З. а) (х — 4)(х + 8) < О

в) 9х(5х — l2) S 0 их 2,4

9х.5(х - 2,4) их * 2,4

х

[0, 2,4)

20) S о

ДО) = [-34; 20]

После выполнения работы и сдачи работ учащимися проверить решения по заранее выполненным записям на доске или по контрольным карточкам. Провести самоанализ. Разобрать те задания, где было сделано больше всего ошибок.

Домашнее задание: п. 9, № 197, 200 (б) [21; из сборника № 791, 792, 797, 798 [4, с. 1 73]•, повторить п. 8

РЕШЕНИЕ ЗАДАЧ (1 ч)

Урок 25 (итоговый)

Цель: проверить знания, умения и навыки учащихся по теме «Неравенства с одной переменной».

Ход урока

1. Организационный момент.

Используется тест. В начале урока ученики получают тест вместе с таблицей, в которую они заносят свои результаты. В тетради выполняются необходимые расчеты.

Если при проверке выявляются ошибки, то можно просмотреть записи учащихся и выявить причины ошибок.

В тесте представлены все типы квадратных неравенств: имеющие два корня, один или ни одного. При выборе аналитического или графического решения необходимо учитывать знак старшего коэффициента (направление ветвей параболы) и строгость неравенства (включение корней в число решений неравенства).

Обязательная часть теста (№ 1—7) представляет собой набор типичных неравенств, которые должны уметь решать все ученики. Вторая часть (№ 8—10) рассчитана на более высокий уровень подготовки учащихся. Также представлены задания еще более сложные (№11—16). Более важным в этих заданиях является отход от стандартного представления учениками решения неравенства как числового промежутка, потому что решениями неравенства являются единственное число или вся числовая ось без одного числа. II. Т ест «Квадратные неравенства».

Задан ия

Выберите из таблицы графическую интерпретацию для каждого из неравенств 1—4:

       1. -2х² +           12 >0.

з. -0,2х² + х- ' О.

      4. 3х² -           18SO.

Таблица 1

В таблице 2 найдите верное решение неравенства 5, в таблице З — решение неравенства 6:

                                  Таблица 2                                             Таблица З

Подберите графическую интерпретацию решения неравенства 7 по таблице 4:

Таблица 4

Из таблицы 5 выберите графическую иллюстрацию неравенства 8, из таблицы 6 — графическую интерпретацию неравенства 9:

      8. 2r <.r-.                                            9. 4х2 _ + 9 > О.

                                  Таблица 5                                             Таблица б

Какое из множеств, указанных в таблице 7, является решением неравенства:

Таблица 7

В таблице 8 найдите графическую интерпретацию неравенств: ll. x² + 2r+ I 13. x² + 2r + О.

   12. -x2-2r- l <O.                           14. 20.

Таблица 8

В таблице 9 найдите решение неравенства 15, в таблице 10 —решение неравенства 16:

         15. -6х+ 9 > О.                              16. —х² + 6х—92 О.

Таблица 9

Лист результатов:

Домашнее задание: № 198 (д, е), 199 (а, г), 201 (а) [2].

     гл              П. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ

(22 часа)

 5. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ

тема (и. 10): ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ (2 ч)

Цел и: обобщить и углубить сведения об уравнениях, ввести понятие целого рационального уравнения и его степени: сформировать НаВЫКИ решения рациональных уравнений с помощью разЛОЛж•еНИЯ на ^м ножители.

Урок 26

Ход урока

1. П роверка домашней работы.

Осуществляется по записям, заранее выполненным на доске.

№ 198 (д, с).

- 36)

-r(x 15)(.r — б)(х + 6) <0

— нули функции 15)(.r — + 6).

          хе                —3)U  (6; 15)

        Ответ: д)             —3)U+0); е) (0, 15).

199 (а, г).

                                                                 г) (х +                    — 21)

      При -^гпооом значении х               х — _7: 4; 21 — нули функции

2 0 и (х —

1)                      2 0 и

2)                      решения данных неравенств различны, значит, они не равносильны.

х-.з

         Ответ: неравенства              20 и (х— З)(х + l) 0 не равносильны.

11. Анализ теста «Квадратные неравенства». Рассмотреть типичные ошибки.

Ш. Изучение нового материала.

Учащиеся самостоятельно изучают п. 10 «Целое уравнение и его корни» и отвечают на во п ро с ы (устно):

1 ) Какие уравнения называются целыми?

2) Приведите примеры целях уравнений.

З) Что называется степенью уравнения?

4)                     Сколько корней имеет уравнение п-й степени?

5)                     Назовите методы решения уравнений первой, второй, третьей и четвертой степеней.

IV. Тренировочные упражнения.

№ 203 — устное решение.

№ 204, 206, 208 — решение на доске, с объяснением.

№ 79 (1) из сборника [4, с. 103]. В ходе диалога с классом выяснить, какой метод решения уравнения применим. Учащиеся сам о стоя тел ь но решают задание. Решение проверяется, необходимые записи выполняются учителем на доске. Итог урока.

Устн ы й о п рос:

1)    Какое уравнение с одной переменной называется целым? Приведите пример.

2)    Как найти степень целого уравнения? Сколько корней может иметь уравнение с одной переменной первой степени, второй степени?

Домашнее задание: п. 10, контрольные вопросы 1, 2 [2, с. 66], № 205, 207, 209; из сборника № 79 (2) [4, с. 103].

Урок 27

Ход урока

1. Актуализация знаний.

1. Индивидуальные зада ни я:

Ответы :

                                2) (-3,5; -2) U (2; +ф).,

      4) (—2; 10);                                      

2. Устные упражнения:

1)  Какова степень уравнения:

а) х² -3х⁵ +2=0; 6) 4х-8 +6) +21;

в) (х² —3) + 5х(х+ 1) = 15?

2)  Является ли число 0; —1;    корнем уравнения:

а) х² — = 0; б)х(х— = О;

З. Самостоятельное изучение п. 10. Целое уравнение и его корни: пример 2 [2, с. 60, 61].

Н. Тренировочные упражнения.

№ 210 (а, в), 212 (а, в) — самостоятел ь ное выполнение заданий в тетрадях и одновременное решение каждого номера двумя учениками на откидных досках. Проверка решения.

№ 213 (а, в, д, ж) — решение у доски, с объяснениями.

№ 81 (1) из сборника [4, с. 103] — решение у доски, с объяснением.

Ш. Итог урока.

Тренировочные упражнения выполняются самостоятельно. Устная проверка ответов.

1.                     Какие из чисел —3; —2; —1; 0; 1; 2; З являются корнями уравнения х• —4х = 0?

2.                     Определите степень уравнения:

         a).r⁵ + 3х⁶ -.r³ + = O•, 6)                              8) = О,

       в)          +4)- (х -                 1) = З: г) (Р                           1) - З(х⁵ -2)

Домашнее задание: п. 10, № 210 (б, г), 212 (б, г), 214; из сбор-

(2) [4, с. 103].

Тема (п. 11): УРАВНЕНИЯ, ПРИВОДИМЫЕ

К КВАДРАТНЫМ (3 ч)

Цели: сформировать умения решать уравнения, приводимые к квадратным, путем введения вспомогательной переменной.

Урок 28

Ход урока

1.  Устные упражнения.

. Разложить на множители:

а) 169-36х²; 6) 1-6х+ 9х²; в) 5х — х^ы; г) х(х— 1) + х²(х — 1).

2.  Решить уравнение:

- 16; 6) 2х³ =16•, в) 3х² + 7 =0.

П. Фронтальный опрос.

Ответить на контрольные вопросы 1, 2 [2, с. 66].

Ш. Самостоятельная работа.

ВАРИАНТ

1.                      Какие из чисел —3; —2; —1; О; 1; 2; З являются корнями уравнения х- — 4х = О?

2.                      Решить уравнение:

                           а) 10, 6) (3х+                                   -3х(3х+ 1) = 5;

       в)                                    г) (6х— l)(x+ 1) = 20.

               4           з        4

ВАРИАНТ

1.                    Какие из чисел —3; —2; —1; О; l •, 2; З являются корнями уравнения х- —9х = О?

2.                    Решить уравнение:

г) (2х — З)(х + 1) —- х- + 17. 5         2 Ответы:

                    Вариант                                        Вариант П

1. -2; о; 2.

5

в) 1 ² ,

IV.  Изучение нового материала.

1. Рассмотреть решение уравнения из примера I [2, с. 63, 64]. 2. Дать определение биквадратного уравнения.

3. Рассмотреть решение уравнения из примера 2 [2, с. 64, 65].

V.     Закрепление.

№ 220 (а, 6), 222 (а, 6, в).

VI.  Итог урока.

В ходе беседы с классом выяснить методы решения целых уравнений: Р(х) = 0, где Р(х) — многочлен стандартного вида.

1.                     Разложение левой части уравнения на множители с помощью: а) вынесения общего множителя за скобки; б) использования формул сокращению умножения; в) метода группировки.

2.                     Введение новой переменной.

Домашнее задание: п. 1 1, № 220 (в, г), 221; из сборника № 73 [4, с. 102].

Урок 29

Ход урока

1. Проверка домашней работы.

11. Устные упражнения. 1 . Решите уравнение:

а) х² + 7х + 6 = 0; б) у⁴ + 7у² + 6 = 0; в) (х² + + 2х + 2) = —1.

2. Решите неравенство:

         а) 5х- S 0; 6) З              О, (х-        + 3,5) < О; г) (2

Ответы:

1: а) —6; —1; б) нет решения; в) —1 .

         ; в) (-3,5; 4); г)         2).

111. Тренировочные упражнения.

№ 222 (г, д, е), 223 (а—в), 226 (а); из сборника № 75 (1) [4,

с. 102] — решение у доски с объяснением.

IV. Итог урока.

Самостоятельная работа.

ВАРИАНТ

1.                     Решите уравнение: а) 9х³ — 27х² = 0; б) х^з —4х² — 9х + 36 = О.

2.                     Решите уравнение, используя введение новой переменной: (Р - - 7) -45 = о.

З. Решите биквадратное уравнение х⁴ — 13х² + 36 = О.

ВАРИАНТ II

1.                     Решите уравнение: а) 18у^з — 36у² = 0; б) 16х³ — 32х² — х + 2 = О.

2.                     Решите уравнение, используя введение новой переменной: (х² - 10)² - 3(х² - 10) -4 = О.

З. Решите биквадратное уравнение х⁴ — 10х² + 9 = О.

Решения:

Вариант

1. а) 9х³ -27х 9х²(х - 3) = о

х = О или х— З = О х = 0 или х = З;

б) х^з — 4х2-9х+36=0 (х^з — 4х ) — х2(х — 4) —9(х — 4) = О (х — 4)(х

(х — 4)(х —

Вариант II

1. а) 18у^З -З6у² =О

18y²0 - 2) = о

У = 0 или у —2 = О У = О или у = 2;

6) 16х³ -32х² -4+2=0

(16х³ - 32х²) - (х- 2) = о

4

Пусть х- — 7 = 1, тогда

д

 = 4 + 45 = 49

4

или х² — 7 = —5

16 или х- = 2

+4 или .r • з. л-⁴ - + 36 = о.

Пусть х² = 1, тогда Р- + 36=0 д: 169- 144= 25

13± 5

х- = 9 или х- = 4

Ответ:

2. - 10) ² - зо^р - Ш) -

Пусть х- l() 1, тогда t- —31-4 = 0 Д = 9 + 16 =25

.r² — 10 = 4 или . х-² - lO=-l = 14 или х- = 9

Пусть х- = г. тогда

4

х- = 9 или х- — I

Ответ:

Домашнее задание: п. 1, контрольные вопросы [2 с. 66], № 223 225, 226 ИЗ сборника 75 (2) [4, с. 102].

Урок ЗО

Ход урока

1.  Проверка домашней работы.

Ответить на вопросы учащихся.

П. Анализ самостоятельной работы. Разобрать типичные ошибки.

Ш. Устные упражнения.

. Решите уравнение:

625 = O•, б)у^з +2у² +у=О.

2.  Найдите область определения функции:

 б) у = х² —Зх . х ² —3х

Ответ ы :

IV. Тренировочные упражнения.

№ 217 (а, 6), 219 (а, 6), 228, 289 (а, 6), 297 (а, в).

Самостоятельное решение заданий. Ученик, первый правильно решивший одно неравенство (уравнение), записывает его на доске, комментирует решение (отвечает на вопросы одноклассников).

V.    Итог урока.

Ответить на контрольные вопросы [2, с. 66].

Домашнее задание: S 4, 5 — подготовиться к контрольной работе, № 7 (в, г), 219 (в, г), 289 (в, г), 297 (6, г) [2].

Урок 3 1

КОНТРОЛЬНАЯ РАБОТА 2

ВАРИАНТ

I . Решите неравенство:

                 а) 2х² — 13х+6                     б)  в) 3х² —6х+ 32

2. Решите неравенство, используя метод интервалов:

x² —1 3х—1 З. Решите уравнение: а) х^з — 81х = 0; б)

                                                                                  2           4

4.       Решите биквадратное уравнение х⁴ — 19х² + 48 = О.

5.       При каких значениях t уравнение 3х² + tx + З = 0 имеет два корня?

6.       Найди те об.ласть определения функции У =

ВАРИАНТ П

1 . Решите неравенст во:

                                               . .-² - 16 < O•. в)х² +              80<0.

Решите неравенство, используя метод интервалов:

           а) (х + l l)(.r—9)           б)

Х ² +6 8

З. Решите уравнение: а) — 25х= 0: б)

5

4.       Реијите биквадратное уравнение х —4х- — 45 = О.

5.       При каких значениях уравнение 2х- + 1х + 8 — 0 не имеет корнеи?

6.       Найдите область определения функции У = 3х-2х ² .

ВАРИАНТ III

1.   Решите неравенс тво:

           а) 2х- + 5х— 7              б) х--25 > 0•, в) 5х- -4х + 21 Я).

2.   Решите неравенство, используя метод интервалов:

З. Решите уравнение а)- ³ - 36х = о•, 6) -v2—4 5х — э З      6

4.       Решитс биквадратное уравнение х -          + 36 = 0.

5.       При каких ЗНаЧСНИЯ.Х уравнение 2х- + 1х + 2 — 0 имеет два корня '?

6.       Найдите область определения функции У =

ВАРИАНТ IV 1 . Решите неравенство:

а) 5х- + 3х - 8 > 0•. 6) х- -49 < 0•, в)

2. Решите неравенство, используя метод интервалов:

л -10

х ² +3 17-3х З. Решите уравнение: а) х-^в —49х = 0; б)

                                                                                    4            8

4.     Решите биквадратное уравнение.•⁴ - 17х² + 16 =0.

5.     При каких значениях уравнение 25х- + [х + I = 0 не имеет корней?

6.     Найдите область определения функции у = 5х — 2х ³

Решение:

Вариант 1.

а) 2х² - 13x+ 6 <O.

у = 2х² — 13x + 6 — квадратичная функция, график — парабола, ветви которой направлены вверх:

Д- 169-48 = 121

13± l l

 4

2

Парабола пересекает ось х в двух точках,

2

1

абсциссы которых равны 6 и

2 '

у  х² — 9 — квадратичная функция, график — парабола, ветви которой направлены вверх:

              Х = 2-3.                                                                                 

Парабола пересекает ось х в двух точках, абсциссы которых равны —3; З;

в) 3х² + (х + 32 > О.

у = 3х- + 6х + 32 — квадратичная функция, график парабола, ветви которой направлены вверх:

                  3х²                          32 = о

9             87<0 4

Парабола не пересекает ось х.

                      Ответ: а) ; —3)U (З; -}-ф)•, В)              +00).

2.

а) (х + 8)(х — 4) > О. х = —8; 4 — нули функции

            У = (х + 8)(х — 4).                    х = —7; 5 — нули функции

(...-оо•, —8) (4; -40 )

Ответ: а) (-оо; —8)U (4; з.

x² —1 3х—1

а) х^з — 81x = О.      6) х(х² — 81) = О      2 4 х(х — 9)(х + 9) = О 2х(х² — 1) —(3х- = 2-4

2х² -2-3— 1 -8=0

2х² -3х-9=0

Д = 9 + 70 - = 81 > O.

4

= -1,5. Ответ: а) —9; 0; 9; б) —1,5 З

          4.х⁴ -      +48 = о.

Пусть х² = г, тогда t² — 19t + 48 = О д: 361 - 192 = 169

19 ± 13

2

= 16, ц = з х 16 или х- = З

Ответ: —4; — ф; $ ; 4.

д, Р - 36.

Уравнение имеет два корня, еслиД> 0.

Р -36>0

(t — 6)(t + 6)

               = — нули функции у = (1 —       + 6).

Ответ: «—6 и t> 6.

          x(l — х) 20                                              

           х = 0; — нули функции g =          1).

Ответ: ДО) = [0; 1].

Вариант 1.

а) 2х ² — 15 <O.

у = 2х² — х — 15 — квадратичная функция, график — парабола, ветви которой направлены вверх:

2х--х-

Д:  121 l ± l l

4 х

Xl = З, Х2 = —2,5.

Парабола пересекает ось х в двух (З; +00) точках (—2,5; 0) и (3; 0);

6)? - 16<O.

— 16 — квадратичная функция, график — парабола, ветви которой направлены вверх:

х² = 16

Парабола пересекает ось х в двух точках (—4; 0) и (4; 0);

в) х² + 12х + 80 < О.

у = х- + 12r + 80 — квадратичная функция, график — парабола, ветви которой на-

правлены вверх:

                     х²                              80 = О

= 36 — 80 = —44 < О.

4

Парабола не пересекает ось х. Нет решений.

                 а) (х + ll)(x — 9)                         

х = —3; 8 — нули функции

У = (х + З)(х — 8)

х (—00', —3) U (8; +00)

Ответ: а) (—1 1; 9);

                з.                                                         .r ² +6 8—х

а) - 25х = о 6)         х(х² - 25) = о          5

=2(х² + б) (8 — х)

                  х(х —         + 5)

2х² + х — 6 = О

                                                                 Д = +48 = 49

4

Ответ: а) —5; 0; 5;

4.   х4 — 4х2 — 45 = О.

Пусть х² = t, тогда t² —4t —45 = О.

Ц = 4 + 45 = 49

4

х- = 9 или х х = ±З, нет решений. Ответ: ±З.

5.   2x² +tx+8 =O. д = Р - 64.

Уравнение не имеет корней, если Д < О.

Ответ: —8 < 8.

6.   у = 3х—2х² 3х - 2х² 2 о

х(2х - 3) S о х = 0; — нули           [0, 1,5] функции g = х(2х — З).

Ответ: ДО) = [0; 1,5].

Вариант III 1.

а) 2х² + 5х — 7 < О.

у = 2х² + 5х 7 — квадратичная функция, график парабола, ветви которой направлены вверх:

2х² + 5х-7=0 д: 25 + 56

4

= -3,5.

Парабола пересекает ось абсцисс (-3,5; 1) в двух точках (—3,5; 0) и (l ; 0);

6) -25 >0.

у = х² — 25 — квадратичная функция, график — парабола, ветви которой направлены вверх:

4 Ковалева

х- - 25 х² = 25

Парабола пересекает ось абсцисс в двух точках (—5; 0) и (5; 0);

в) 5х² — 4х + 21 > О.

у = 5х- —4х + 21 — квадратичная функция, график — парабола, ветви которой направлены вверх:

5.r--4x + 21

Ц, 4 — 105 - — —lOl < O.х 4

Парабола не пересекает ось абсцисс.

Ответ: а) (—3,5; l ); б) (—0

2.

х = —9; 5 — нули функции               х = —6: 3 — нули функции

(—оо•, _9)U (5; +00)

Ответ: а) (—..o.,

з.

а) х^з 36х = 0. .r(x² - 36) = о x(.r — б)(х + 6) = 0

Ответ: а) —6; 0: 6;

—6

(5,

.r ² -4 5х-2

6) з  6

2(х2 — 4) — (5х — 2) = 6

+2-6=0 2х- -5х- 12 = 0 д: 25 + 96= 121.

5 ± l l

4

_kl = 4; хэ — —1,5.

6)

4. ё- 13х² + 36 = о.

Пусть .х² = t, тогда t² — 13t 36 д: 169- 144 = 25

13±5

2

х- = 9 или х² = 4

- 2.

Ответ: —3; —2; 2; З.

5. 2х² +tx+2=O. д: Р- 16.

Уравнение имеет два корня, еслиД> О.

Р— 16>O

         = — нули функции у = (t —        + 4).

     Ответ:          и» 4.

2х-х2 2х-х220      

х = 0; 2 — нули функции g = х(х — 2). Ответ: ДО) = [О; 2].

Вариант IV 1.

а) 5х² + 3х — 8 > О.

у = 5х² + 3х — 8 — квадратичная функция, график — парабола, ветви которой направлены вверх:

5х² + 3х — 8 = О д=9+ 160 = 169

—3± 13

10

= l,X2 = —1,6.

Парабола пересекает ось абсцисс       в двух точках (—1,6; 0) и (1; 0);

6) -49 <0.

у = х² — 49 квадратичная функция, график парабола, ветви которой направлены вверх:

х2 — 49 = О х² = 49

Парабола пересекает ось х в двух точках, абсциссы которых равны —7; 7;

в) 4х² -2х+ в у = 4х- — 2х + 13 — квадратичная функция, график — парабола, ветви которой направлены вверх:

4х² -2х+ в

52 51 < O.

4

Парабола не пересекает ось абсцисс.

Нет решений.

     Ответ: а) (—оо; —1     (1; +O•, б) (—7; 7); в) нет решений.

2.

      6) х = —12; 7 — нули функции  x-lO

                        х = —5; 10 — нули функции

Ответ: а) (—12; 7); б) (—0

З.

2х² + 6- 17 +3х- 16=0

2х2 д, 9 +

—3± 15

4

 = З; = 4,5.

Ответ : а) —7; о; т, 6) з; 4,5.

4.  х⁴ — 17х

Пусть х² = t, тогда t

д = 289-64 = 225

17±15 2 tl = 16, Ь = ¹ .

х = 16 или х- =

—4, Х2 = 4, Х3 = —l,x4 Ответ: —4; —1; 1; 4.

5.  25х² +tx+ д-р- 100.

Уравнение не имеет корней, еслиД< 0. Р- lOO<O

5х — 2х² О

х = 0; 2,5 — нули функции [0; 2,5] = х(2х- 5).

Ответ: ДО) = [0, 2,5].

2. СИСТЕМЫ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ

Тема (п. 12): ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ (4 ч)

Цели: завершить изучение уравнений с двумя переменными; сформировать умения графически решать системы уравнений, привлекая известные учащимся графики; дать наглядные представления, что система двух уравнений с двумя переменными второй степени может иметь одно, два, три, четыре решения, может не иметь решений.

lOl

Урок 32

Ход урока

1. Анализ контрольной работы.

Рассмотреть типичные ошибки, показать правильное решение, ответить на вопросы учащихся по контрольной работе. П. Повторение.

ВАРИАНТ 1- № 241 (а).

ВАРИАНТ - № 242 (а).

Самостоятельное решение. Одновременно двое учеников решают задания на доске. Устный разбор решений.

Ш. Изучение нового материала.

1.    При мер ы уравнений с двумя переменными.

2.    Определение графика уравнения с двумя переменными.

3.    Напомнить изученные ранее графики:

а) графиком уравнения ах + ву = с, где а, в, с — некоторые числа, является прямая;

б) графиком уравнения у = ах- + вх + с. где а, в, с — некоторые числа, а 0, является парабола;

в) графиков уравнения у   (ху = 1) является гипербола; х

г) графиков уравнения (х — + (у — = R- является окружность с центром в точке (а; в) и радиусом R

4.    Понятие степени целого уравнения с двумя переменными. Пример: (х^з + у) 2 - - 6 - 1.-- r

2хУ + у- + = О Степень уравнения равна 4.

5.    Графическое решение системы уравнений:

6.    Графический способ решения систем уравнений:

1)    построить в одной системе координат графики уравнений системы;

2)    найти приближенные значения координат точек пересечения графиков;

3)    если возможно, с помощью проверки уточнить решения системы.

102

IV. Тренировочные упражнения.

№ 230 — устное решение.

№ 231 — у доски, по желанию.

№ 232 — устно.

№ 238 (б, в) — двое учащихся решают у доски, комментируют решения.

V.    Итог урока.

Устные упражнения.

1)   Решите систему уравнений:

2)   Какая фигура является графиком уравнения:

а)у=Кх+в; б) х- + у- = R² •, в) у + ах² + вх+с=0; г) ху = 1, где а, в, с, К, R — некоторые числа, а 0?

Домашнее задание: п. 12, контрольный вопрос I [2, с. 76], № 238 (а, г), 240 (а, б) — по желанию, № 241 (б), 242 (б); работа над ошибками контрольной работы.

Урок 33

Ход урока

1. Актуализация знаний.

1 . Индивидуальные зада н и я для слабоуспевающих учеников: 1 ) Определите степень уравнения:

а) 2х+ Зу=6•,

2) Изобразите схематически графики функций:

в) ху = 6; г) ху = —6.

2. Индивидуальные зада ни я более высокого уровня:

1)    Изобразив схематически графики уравнений, выясните, имеет ли решение система уравнений и если имеет, то сколько? х— у² = 36, У = 2х2 — 6.

2)    Покажите с помощью графиков, что система уравнений х^е + у— = 64, ху = 6 имеет четыре решения, и найдите их.

Индивидуальные задания выполняются учащимися во время решения устных упражнений.

З. Устные упражнения.

) Определите степень уравнения:

а) ху—2у=5; б)х² —у=3; в)х² + 3у² = О.

2) Является ли пара чисел (1; О) решением уравнения:

            а)х² + у = 1; б) ху +3 = х;                 2) = О?

З) Что представляет собой график уравнения:

             а)х² +У² = 4; б) (х— l)² +0+                 в) (х + 5)² +0—         О?

4) Объясните, в чем состоит графический способ решения системы уравнений с двумя переменными. П. Тренировочные упражнения.

№ 233, 234, 236.

Перед решением каждого номера в ходе фронтального опроса учащихся наметить план решения, выяснив, что представляет собой график каждого уравнения системы, как его построить, как определить число решений системы, как найти решение системы.

Самостоятельное решение заданий.

Проверка решения у доски; ученик, первым выполнивший решение, записывает его на доске. Ш. Повторение.

№ 240 (в, г).

1V. Итог урока.

V. Разбор домашнего задания.

№ 243 — провести анализ решения текстовой задачи, необходимые записи, план решения записать в ходе диалога с классом на доске и в тетрадях.

Домашнее задание: п. 12, № 237, 243 [2].

Урок 34

Ход урока

1. Проверка домашней работы.

Устно проверить задание.

11. Устные упражнения.

1. Решите неравенство: а) 9 —х² > 0;

6) 16-x² <O.

2. Решите систему уравнений:

З. Как из графика функции у = х² получить график функции:

4. Назовите центр и радиус окружности:

     а) (х —3)² + (у —4)² = 4; б) (х —l0)² +      16;

III. Тренировочные упражнения (с проверкой).

Построить схематически график функции: 5 х

Одновременно с учащимися класса двое учеников выполняют задания за доской. IV. Решение.

      из сборника № 203 (2), 204     205 (2), 206     207 (1) [4, с. 121].

I. Перед выполнением заданий учащиеся отвечают на во п р о с ы : 1) Как построить графики функций:

а) у=б•, б) y=lxl;

г) у = + в, где К и в — некоторые числа, К * О;

2) Как графически решить уравнение из № 207 (1)? (План ре-

ШеНИЯ.)

В ходе беседы с учащимися учитель делает соответствующие записи на доске.

2. Самостоятельное решение. Каждый ученик может обратиться к учителю за консультацией.

З. Проверка решений осуществляется с помощью:

а) контрольных карточек или

б) плакатов с изображением графиков.

Тогда необходимы комментарии к решению.

Контрольные карточки 203 (2). у=сх, ху— 8 = О.

ху = 8, график уравнения — гипербола.

Ответ: (4; 2).

№ 204 (1).

+ 2х² = З. 1) y=lxl.

      х у = —2х² + З — квадратичная функция, график — парабола, ветви которой направлены вниз. (0; З) — координаты вершины параболы. х = 0 — ось симметрии. • 1), во; 1)

Ответ: (—1; 1), (1; 1).

 205 (2). ху = 2,

1) ху = 2. график уравнения — гипербола;

 — —х2 + 4 — квадратичная функция, график — парабола, ветви которой направлены вниз.

График функции у = —х² + 4 получатся из графика функции у = --х с помощью параллельного переноса вдоль оси у на 4 единицы вверх.х

= —2,2, у = —0,9; = 0,5, п - 3,7; 1,8,   l,l.

ответ: (-2,2, -0,9), (0,5; 3,7), (1,8; 1,1).

2) ху = 4, график уравнения — гипербола.

Графики функций пересекаются в двух точках. Значит, система уравнений имеет два решения. Ответ: 2 решения. 207 (1).

0х-8 +

Рассмотрим функции у и у = —1,5х + 8 и построим их графики. 1) уза.

2) у = —1,5х + 8 — линейная функция, график — прямая.

Ответ: 4.

V. Итог урока.

1.    Учащиеся проводят самоанализ. (Какие задания вызвали затруднения?)

2.    Повторить, в чем заключается графический способ решения системы уравнений с двумя переменными.

Домашнее задание: из сборника № 203 (1), 204 (2), 205 (1), 206 (2), 207 (2) [4, с. 121].

Урок 35

Ход урока

1. Актуализация знаний.

Сообщение учащимся цели урока. Проверка знаний по теме «Графический способ решения систем уравнений», хода урока.

11. Тренировочное упражнение.

Из сборника № 208 (1) [4, с. 12 (решение у доски, с объяснением).

111. Самостоятельная работа.

ВАРИАНТ

I . Решите графически уравнение х

2. Найдите с помощью графиков число корней уравнения

З. Решите графически систему уравнений: У = х2 — 2х — 4,

4. Найдите с помощью графиков число решений системы уравнений:

У = —(х + 2)², ху = З.

ВАРИАНТ

1 . Решите графически уравнение х^з = (х — 2)

2. Найдите с помощью графиков число корней уравнения Cx=-x2+4x-l.

З. Решите графически систему уравнений:

4. Найдите с помощью графиков число решений системы уравнений:

Ответы:

         4. Одно решение.                     4. Три решения.

Другой вариант самостоятельной работы.

ВАРИАНТ 1

1.                      Решите графически систему уравнений:

       а) ху = 8,                   6) у=х² -2,                    в) х² +у² = 25,

2.                      Изобразив схематически графики, выяснить, имеет ли решения система уравнений и если имеет, то сколько:

ВАРИАНТ П

1 . Решите графически систему уравнений:

      а) ху = 4,                6) у: 0,5х²,                   в) х² +у² = 16,

                       —x= l;                

2. Изобразив схематически графики, выясните, имеет ли решения система уравнений и если имеет, то сколько:

Ответы:

             Вариант                                                 Вариант II

                             1: а)  (1,6; 2,6);

         6) (2,1; 2,5);                                  6) (-0,8; 0,2); (2,2; 3,2);

                        в) (-2,8; 2,8); (2,8; -2,8);

2. Система имеет два решения. 2. Система имеет два решения.

Домашнее задание: из сборника № 208 (2), 209, 210, 21 1 (1), 212 (1) [4, с. т, 122].

Тема (п. 13): РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ

ВТОРОЙ СТЕПЕНИ (4 ч)

Цели: сформировать умения решать системы уравнений второй степени с помощью способов подстановки и сложения, особое внимание уделить системам, в которых одно уравнение первой степени, а другое — второй.

Урок 36

Ход урока

1.  Анализ самостоятельной работы.

. Разобрать типичные ошибки.

2.  Ответить на вопросы учащихся.

З. З ада н ие ученикам: выполнить и сдать на проверку работу над ошибками.

11. Изучение нового материала.

Рассмотрим один из аналитических способов решения систем уравнений: способ подстановки.

1.    Решим систему уравнений первой степени: из сборника

№ 525 [4, с. 159].

2х+Зу= З,

5х + бу = 9.

Окончание табл.

2.    Решим систему уравнений второй степени. Пример I из

п. 13 [2, с. 70].

х- — 3ху — 2у- = 2,

Во п рос ы классу:

1)    Какую переменную, из какого уравнения системы нужно выразить?

2)    Каковы дальнейшие шаги? Решение:

              х² — 3ху — 2у² = 2,                х2 — 3ху — 2у2 = 2,

   x+2y= l                      l —2y

1)  (1 - - 3y(l - 2у) -2у² = 2.

2-2у 8y2-7y- l =O

д = 49 + 32 = 81

16

8

Ответ: (—1; 1) l ^L ; -L .

4    8 l ll

2)  х = I —2у.

1

4

З. Составить алгоритм решения системы уравнений способом подстановки (с. 70).

Ш. Тренировочные упражнения.

1.    Устное задание: выразить одну переменную через другую из уравнения:

а) 4х—2у= 6; б) 3х +4у=2; в) 2х + Зу = —7; г) 2х—3у=—5.

2.    Решение у доски, с объяснением № 244 (а, в); 246 (а, в); 248 (а, г, д); из сборника № 104 (1) [4, с. 106].

IV.                      Самостоятельное решение на повторение, с проверкой. № 265 (а, 6).

V. Итог урока.

Повторить алгоритм решения системы уравнений способом подстановки.

Домашнее задание: п. 13, контрольный вопрос 2 [2, с. 76], № 245 (а, г), 247 (г), 248 (е); из сборника № 104 (2) [4, с. 106].

Урок 37

Ход урока

1.  Проверка домашней работы.

Устно проверить ответы к заданиям домашней работы, повторить алгоритм решения систем уравнений способом подстановки.

П. Решение.

№ 244 (6, г), 245 (6, в), 246 (6, г).

Трое учащихся решают задания у доски, с последующими устными комментариями после выполнения классом устных упражнений.

Ш. Устные упражнения.

. Определите степень уравнения:

а) 5х—3ху= 8;  1; в)2у² +х²у= О.

2.  Имеет ли решения система уравнений

З. Выразите одну переменную через другую:

а) х2 + у— 5 = 0; б) х +2у+ху=4.

112

4. Найдите решения системы уравнений: У = —х^[4] + 4,

= 3х². Ответы:

1: а) вторая; б) вторая; в) третья;

2. а) нет; б) нет;

² 4—2у  4—х ;   5—х; б) х =

IV. Решение.

№ 249 (а, в, е), 250 (а), 252 (а), 253.

V.    Итог урока.

Наметить план решения № 254, заданного на дом.

Домашнее задание: № 251, 254; из сборника № 105 [4, с. 106].

Урок 38

Ход урока

1.    Проверка домашней работы.

Проверить ответы к заданиям № 25 1, 254.

Проверить решение № 105 (1) из сборника, по записям, заранее зыполненным на доске.

— ху = 12 —у²,

²

 (2; —2).

11. Устные упражнения. I . Решите систему уравнений:

2.    При каких значениях х имеет смысл выражение 2х—х ² ? ответы: 1. (3; 4), 2). 2. [0, 2].

Ш. Тренировочные упражнения. № 255 (6), 257 (а, 6), 259.

IV. Итог урока.

Самостоятельная работа.

ВАРИАНТ

1 . Является ли пара чисел х = 6, у= —8 решением системы уравнений:

3х+ 2у-2=О?

2. Решите систему уравнений:

б) х2 —у2 = 24, в) (х— 1) = 30.  2х-у= Ш.

ВАРИАНТ ll

. Является ли пара чисел х = 7, у = —6 решением системы уравнений:

ХУ + 42 = О, x--2y-61 = 0?

2. Решите систему уравнений:

а) х- -2у= 54,24,

Ответы:

                           Вариант I                                  Вариант II

              1. да.                                                1. Да

                   , —94; —82 .                

, -L ;- l l

2

Домашнее задание: № 256 (а), 257 (в), 260 [2].

Урок 39

Ход урока

1. Организационный момент.

11. Изучение нового материала.

1. Рассмотреть способ сложения, применяемый при решении систем уравнений.

1)     Решим систему уравнений первой степени. из сборника № 525 [4, с. 159]. 2х + Зу = З, 5х + бу = 9.

2)     Решим систему уравнений второй степени.

х + Зу = l l ,

У2-6у+8=О

Ответ: (—1; 4), (5; 2).

2. Составить алгоритм решения системы уравнений способом сложения:

1)                    Ульчолсшпь почленно уравнения системы. помирая .МПОЭЮИптак•, чтобы коэффициенты при оДноЙ из переменных стали противоположными чис.лаии.

2)                    Стожить почленно правые и левые частн уравнений системы.

З) Решить полученное уравнение.

4) Найти соответствующие ЗНСIЧШшЯ второй переменной.

3.    Рассмотреть пр и мер 2 из п. 13 [2, с. 71].

Ш. Тренировочные упражнения. № 261, 262, 263 (6, г), 264

lV. Итог урока.

Решить устно.

1 . Решить систему уравнений: