Добавить материал

и получить 10 документов
и свидетельство автора

Рыбинок Екатерина Валерьевна

PHY_10_38_V2_TG_Capacit.energy

docx
07.05.2020

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

PHY_10_38_V2_TG_Capacit.energy.docx

Recommendation

on lesson “Energy stored in a charged capacitor”

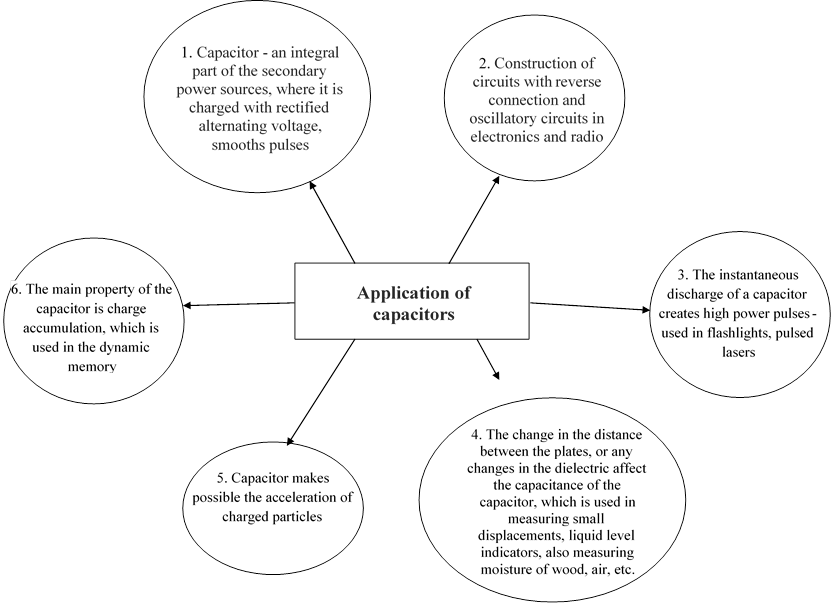
In this lesson Reading task activity can be organized differently. For example, one group can use printed text and do the reading task. The second group can investigate and find information by themselves by using the internet resources. However, is there is no access to the internet, teacher might spread out applications from the article and students working in small groups read only one application and present it. During the poster presentation teacher add some more applications from the slides or use Attachment 1.

During watching a video clip teacher might stop at any time and make sure that students are getting well with it. There is also option during this activity. Each group can look for answer of only one question. More able student will be given an extended question about energy stored in series of capacitors. If class English level is not enough to understand the topic, teacher can give them model answer (Attachment 2) and ask them explain what they have understood.

Teacher can replace homework problems so students solve them in a class and the problems from the slide 12 solve at home.

Theoretical material: Energy stored in a charged capacitor

Most of us have seen dramatizations in which medical personnel use a defibrillator to pass an electric current through a patient’s heart to get it to beat normally. Often realistic in detail, the person applying the shock directs another person to “make it 400 joules this time.” The energy delivered by the defibrillator is stored in a capacitor and can be adjusted to fit the situation. SI units of joules are often employed. Less dramatic is the use of capacitors in microelectronics, such as certain handheld calculators, to supply energy when batteries are charged.Capacitors are also used to supply energy for flash lamps on cameras.

Energy stored in a capacitor is electrical potential energy, and it is thus related to the charge $\boldsymbol{Q}$ and voltage $\boldsymbol{V}$ on the capacitor. We must be careful when applying the equation for electrical potential energy $\boldsymbol{\Delta \textbf{PE} = q \Delta V}$ to a capacitor. Remember that $\boldsymbol{\Delta \textbf{PE}}$ is the potential energy of a charge $\boldsymbol{q}$ going through a voltage $\boldsymbol{\Delta V}$ . But the capacitor starts with zero voltage and gradually comes up to its full voltage as it is charged. The first charge placed on a capacitor experiences a change in voltage $\boldsymbol{\Delta V = 0}$ , since the capacitor has zero voltage when uncharged. The final charge placed on a capacitor experiences $\boldsymbol{\Delta V = V}$ , since the capacitor now has its full voltage $\boldsymbol{V}$ on it. The average voltage on the capacitor during the charging process is $\boldsymbol{V/2}$ , and so the average voltage experienced by the full charge $\boldsymbol{q}$ is $\boldsymbol{V/2}$ . Thus the energy stored in a capacitor, $\boldsymbol{E_{\textbf{cap}}}$ , is

$\boldsymbol{E_{\textbf{cap}} =}$ $\boldsymbol{\frac{QV}{2}} ,$

where $\boldsymbol{Q}$ is the charge on a capacitor with a voltage $\boldsymbol{V}$ applied. (Note that the energy is not $\boldsymbol{QV}$ , but $\boldsymbol{QV/2}$ .) Charge and voltage are related to the capacitance $\boldsymbol{C}$ of a capacitor by $\boldsymbol{Q = CV}$ , and so the expression for $\boldsymbol{E_{\textbf{cap}}}$ can be algebraically manipulated into three equivalent expressions:

$\boldsymbol{E_{\textbf{cap}} =}$ $\boldsymbol{\frac{QV}{2}}$ $\boldsymbol{=}$ $\boldsymbol{\frac{CV^2}{2}}$ $\boldsymbol{=}$ $\boldsymbol{\frac{Q^2}{2C}},$

where $\boldsymbol{Q}$ is the charge and $\boldsymbol{V}$ the voltage on a capacitor $\boldsymbol{C}$ . The energy is in joules for a charge in coulombs, voltage in volts, and capacitance in farads.

In a defibrillator, the delivery of a large charge in a short burst to a set of paddles across a person’s chest can be a lifesaver. The person’s heart attack might have arisen from the onset of fast, irregular beating of the heart—cardiac or ventricular fibrillation. The application of a large shock of electrical energy can terminate the arrhythmia and allow the body’s pacemaker to resume normal patterns. Today it is common for ambulances to carry a defibrillator, which also uses an electrocardiogram to analyze the patient’s heartbeat pattern. Automated external defibrillators (AED) are found in many public places (Figure 2). These are designed to be used by lay persons. The device automatically diagnoses the patient’s heart condition and then applies the shock with appropriate energy and waveform. CPR is recommended in many cases before use of an AED.

Attachment 2

Attachment 2

1. Why the light bulb lights up when it connected with a capacitor?

Charged capacitor is stores energy. When a charged capacitor connected to a light bulb, energy turns into light and heat energy.

2. What kind of energy stored in a capacitor?

Capacitor stores electric potential energy

3. How do we calculate the energy stored in a capacitor?

E=1/2 QV

4. What is the significance of the coefficient ½ in a capacitor energy equation?

During discharging not all of the charges drop through the total initial voltage V. In fact only the first charge that gets transferred is going to drop through total initial voltage V. All of the charges that get transferred after are going to drop through less and less voltage. The reason for this is that each time charges get transferred it decreases the total amount stored on the capacitor. As charges on the capacitor keeps decreasing, the voltage of the capacitor keeps decreasing as well. As more and more charge gets transferred, there will be a point where a charge only drops through ¾ of the initial voltage. Wait longer and when a charge gets transferred through only a half of the initial voltage V, than ¼ of the initial voltage V and so on. And last charge to get transferred drops through almost no voltage at all, because there is basically no charge left that’s stored in a capacitor. If we add up all of these drops in electrical potential energy, you would find that the total drop in energy of the capacitor E=Q V/2

So, on average the charges dropped through only a half the initial voltage.

5. What are the alternative equations for the capacitor energy?

E=1/2CV²

E=1/2 Q² C

Extended part: (from 5.45min)

1. How do we calculate the energy stored in a capacitor for a multiple capacitors connected in a circuit?

In order to find the energy of the single capacitor, we have to use the voltage across that particular capacitor (and not the battery)

Additional problems with solutions: Low level

1: (a) What is the energy stored in the $\boldsymbol{10.0 \;\mu \textbf{F}}$ capacitor of a heart defibrillator charged to $\boldsymbol{9.00 \times 10^3 \;\textbf{V}}$ ? (b) Find the amount of stored charge.

2: In open heart surgery, a much smaller amount of energy will defibrillate the heart. (a) What voltage is applied to the $\boldsymbol{8.00 \; \mu \textbf{F}}$ capacitor of a heart defibrillator that stores 40.0 J of energy? (b) Find the amount of stored charge.

3: A $\boldsymbol{165 \;\mu\textbf{F}}$ capacitor is used in conjunction with a motor. How much energy is stored in it when 119 V is applied?

4: Suppose you have a 9.00 V battery, a $\boldsymbol{2.00 \;\mu \textbf{F}}$ capacitor, and a $\boldsymbol{7.40 \;\mu \textbf{F}}$ capacitor. (a) Find the charge and energy stored if the capacitors are connected to the battery in series. (b) Do the same for a parallel connection.

5: A nervous physicist worries that the two metal shelves of his wood frame bookcase might obtain a high voltage if charged by static electricity, perhaps produced by friction. (a) What is the capacitance of the empty shelves if they have area $\boldsymbol{1.00 \times 10^2 \;\textbf{m}^2}$ and are 0.200 m apart? (b) What is the voltage between them if opposite charges of magnitude 2.00 nC are placed on them? (c) To show that this voltage poses a small hazard, calculate the energy stored.

6: Show that for a given dielectric material the maximum energy a parallel plate capacitor can store is directly proportional to the volume of dielectric ( $\boldsymbol{\textbf{Volume} = A \cdot d}$ ). Note that the applied voltage is limited by the dielectric strength.

Additional problems with solutions: High level

7: Construct Your Own Problem

Consider a heart defibrillator similar to that discussed in Example 1. Construct a problem in which you examine the charge stored in the capacitor of a defibrillator as a function of stored energy. Among the things to be considered are the applied voltage and whether it should vary with energy to be delivered, the range of energies involved, and the capacitance of the defibrillator. You may also wish to consider the much smaller energy needed for defibrillation during open-heart surgery as a variation on this problem.

8: Unreasonable Results

(a) On a particular day, it takes $\boldsymbol{9.60 \times 10^3 \;\textbf{J}}$ of electric energy to start a truck’s engine. Calculate the capacitance of a capacitor that could store that amount of energy at 12.0 V. (b) What is unreasonable about this result? (c) Which assumptions are responsible?

9. A heart defibrillator delivers $\boldsymbol{4.00 \times 10^2 \;\textbf{J}}$ of energy by discharging a capacitor initially at $\boldsymbol{1.00 \times 10^4 \;\textbf{V}}$ . What is its capacitance?

ANSWERS:

1: (a) 405 J

(b) 90.0 mC

2: (a) 3.16 kV

(b) 25.3 mC

4: (a) $\boldsymbol{1.42 \times 10^{-5} \;\textbf{C}}$ , $\boldsymbol{6.38 \times 10^{-5} \;\textbf{J}}$
(b) $\boldsymbol{8.46 \times 10^{-5} \;\textbf{C}}$ , $\boldsymbol{3.81 \times 10^{-4} \;\textbf{J}}$

5: (a) $\boldsymbol{4.43 \times 10^{-12} \;\textbf{F}}$
(b) 452 V

8: (a) 133 F

(b) Such a capacitor would be too large to carry with a truck. The size of the capacitor would be enormous.

9. We are given E and V, and we are asked to find the capacitance $\boldsymbol{C}$ . Of the three expressions in the equation for E, the most convenient relationship is E=CV²/2

Solving this expression for C and entering the given values yields

This is a fairly large, but manageable, capacitance at $\boldsymbol{1.00 \times 10^4 \;\textbf{V}}$ .

Additional multiple choice questions: Capacitors in Series and Parallel (Average level)

72. Which one of the following statements is true concerning capacitors of unequal capacitance connected in series?

(a) Each capacitor holds a different amount of charge.

(b) The equivalent capacitance of the circuit is the sum of the individual capacitances.

(d) The total positive charge in the circuit is the sum of the positive charges on each capacitor.

(e) The total voltage supplied by the battery is equal to the average voltage across all the capacitors.

73. Three parallel plate capacitors, each having a capacitance of 1.0 µF are connected in parallel.

The potential difference across the combination is 100 V. What is the equivalent capacitance of this combination?

(a) 0.3 mF (c) 3 mF (e) 30 mF

(b) 1 mF (d) 6 mF

74. Three parallel plate capacitors, each having a capacitance of 1.0 µF are connected in parallel.

The potential difference across the combination is 100 V. What is the charge on any one of the capacitors?

(a) 30 mC (c) 300 mC (e) 3000 mC

(b) 100 mC (d) 1000 mC

75. A 3.0-µF capacitor is connected in series with a 4.0-µF capacitor and a 48-V battery. What quantity of charge is supplied by the battery to charge the capacitors?

(a) 3.4 ´ 10^–4 C (c) 3.0 ´ 10^–5 C (e) 1.8 ´ 10^–6 C

(b) 7.3 ´ 10^–4 C (d) 8.2 ´ 10^–5 C

76. What is the equivalent capacitance of the combination of capacitors shown in the circuit?

(a) 0.37 µF (d) 0.67 µF

(b) 3.3 µF (e) 2.1 µF

77. How much energy is stored in the combination of capacitors shown?

(a) 0.01 J (d) 0.04 J

(b) 0.02 J (e) 0.05 J

78. A battery supplies a total charge of 5.0 mC to a circuit that consists of a series combination of two identical capacitors, each with capacitance C. Determine the charge on either capacitor.

(a) 5.0 mC (c) 1.5 mC (e) 0.50 µC

(b) 2.5 mC (d) 1.0 mC

79. When two capacitors are connected in series, the equivalent capacitance of the combination is 100 µF. When the two are connected in parallel, however, the equivalent capacitance is 450 µF. What are the capacitances of the individual capacitors?

(a) 200 µF and 250 µF (d) 150 µF and 300 µF

(b) 125 µF and 325 µF (e) 80 µF and 370 µF

Additional multiple choice questions: Capacitors in Series and Parallel (Average level)

Questions 80 through 82 pertain to the situation described below:

A 10.0-µF capacitor is charged so that the potential difference between its plates is 10.0 V.

A 5.0-µF capacitor is similarly charged so that the potential difference between its plates is 5.0 V.

The two charged capacitors are then connected to each other in parallel with positive plate connected to positive plate and negative plate connected to negative plate.

80. How much charge flows from one capacitor to the other when the capacitors are connected?

(a) 17 mC (c) 67 mC (e) zero coulombs

(b) 33 mC (d) 83 mC

81. What is the final potential difference across the plates of the capacitors when they are connected in parallel?

(a) 5.0 V (c) 7.5 V (e) 10 V

(b) 6.7 V (d) 8.3 V

82. How much energy is dissipated when the two capacitors are connected together?

(a) 33 mJ (c) 63 mJ (e) 560 mJ

(b) 42 mJ (d) 130 mJ

USEFUL resources:

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capac.html#c1

https://tap.iop.org/electricity/capacitors/128/page_46177.html

https://www.electrical4u.com/energy-stored-in-capacitor/

https://www.lifewire.com/what-are-applications-of-capacitors-818986

Скачано с www.znanio.ru

Recommendation on lesson “Energy stored in a charged capacitor”

Today it is common for ambulances to carry a defibrillator, which also uses an electrocardiogram to analyze the patient’s heartbeat pattern

Attachment 2 1. Why the light bulb lights up when it connected with a capacitor?

C are placed on them? (c) To show that this voltage poses a small hazard, calculate the energy stored

How much energy is stored in the combination of capacitors shown? (a) 0

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также