PHY_10_6_V2_TG_Isoprocesses

Theoretical material for the lesson, definitions for concepts 

Boyle's Law

Torricelli's experiment did more than just show that air has weight; it also provided a way of creating a vacuum because the space above the column of mercury at the top of a barometer is almost completely empty. (It is free of air or other gases except a negligible amount of mercury vapor.) Torricelli's work with a vacuum soon caught the eye of the British scientist Robert Boyle.

Boyle's most famous experiments with gases dealt with what he called the "spring of air." These experiments were based on the observation that gases are elastic. (They return to their original size and shape after being stretched or squeezed.) Boyle studied the elasticity of gases in a J-tube similar to the apparatus shown in the figure below. By adding mercury to the open end of the tube, he trapped a small volume of air in the sealed end.

Boyle studied what happened to the volume of the gas in the sealed end of the tube as he added mercury to the open end.

Boyle noticed that the product of the pressure times the volume for any measurement in this table was equal to the product of the pressure times the volume for any other measurement, within experimental error.

P₁V₁ = P₂V₂

This expression is now known as Boyle's Law.

Amonton's Law

Toward the end of the 1600s, the French physicist Guillaume Amontons built a thermometer based on the fact that the pressure of a gas is directly proportional to its temperature. The relationship between the pressure and the temperature of a gas is therefore known as Amontons' law.

P T

Amontons' law explains why car manufacturers recommend adjusting the pressure of your tires before you start on a trip. The flexing of the tire as you drive inevitably raises the temperature of the air in the tire. When this happens, the pressure of the gas inside the tires increases.

Amontons' law can be demonstrated with the apparatus shown in the figure below, which consists of a pressure gauge connected to a metal sphere of constant volume, which is immersed in solutions that have different temperatures.

The following data were obtained with this apparatus.

In 1779 Joseph Lambert proposed a definition for absolute zero on the temperature scale that was based on the straight-line relationship between the temperature and pressure of a gas shown in the figure above.

He defined absolute zero as the temperature at which the pressure of a gas becomes zero when a plot of pressure versus temperature for a gas is extrapolated. The pressure of a gas approaches zero when the temperature is about -270C. When more accurate measurements are made, the pressure of a gas extrapolates to zero when the temperature is -273.15C. Absolute zero on the Celsius scale is therefore -273.15C.

The relationship between temperature and pressure can be greatly simplified by converting the temperatures from the Celsius to the Kelvin scale.

T_K = T^oC + 273.15

When this is done, a plot of the temperature versus the pressure of a gas gives a straight line that passes through the origin. Any two points along the line therefore fit the following equation.

It is important to remember that this equation is only valid if the temperatures are converted from the Celsius to the Kelvin scale before calculations are done.

Charles' Law

On 5 June 1783, Joseph and Etienne Montgolfier used a fire to inflate a spherical balloon about 30 feet in diameter that traveled about a mile and one-half before it came back to earth. News of this remarkable achievement spread throughout France, and Jacques-Alexandre-Cesar Charles immediately tried to duplicate this performance. As a result of his work with balloons, Charles noticed that the volume of a gas is directly proportional to its temperature.

V T

This relationship between the temperature and volume of a gas, which became known as Charles' law, provides an explanation of how hot-air balloons work. Ever since the third century B.C., it has been known that an object floats when it weighs less than the fluid it displaces. If a gas expands when heated, then a given weight of hot air occupies a larger volume than the same weight of cold air. Hot air is therefore less dense than cold air. Once the air in a balloon gets hot enough, the net weight of the balloon plus this hot air is less than the weight of an equivalent volume of cold air, and the balloon starts to rise. When the gas in the balloon is allowed to cool, the balloon returns to the ground.

Charles' law can be demonstrated with the apparatus shown in the figure below. A 30-mL syringe and a thermometer are inserted through a rubber stopper into a flask that has been cooled to 0C. The ice bath is then removed and the flask is immersed in a warm-water bath. The gas in the flask expands as it warms, slowly pushing the piston out of the syringe. The total volume of the gas in the system is equal to the volume of the flask plus the volume of the syringe.

Absolute zero is the temperature at which the volume of a gas becomes zero when the a plot of the volume versus temperature for a gas are extrapolated. As expected, the value of absolute zero obtained by extrapolating the data is essentially the same as the value obtained from the graph of pressure versus temperature in the preceding section. Absolute zero can therefore be more accurately defined as the temperature at which the pressure and the volume of a gas extrapolate to zero.

A plot of the volume versus the temperature of a gas (when the temperatures obtained are converted from Celsius to the Kelvin scale) becomes a straight line that passes through the origin. Any two points along this line can therefore be used to construct the following equation, which is known as Charles' law.

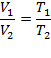
Before using this equation, it is important to remember that temperatures must be converted from C to K.

https://chemed.chem.purdue.edu/genchem/topicreview/bp/ch4/gaslaws.php#ideal

Additional guidelines for organizing a lesson 

- What do you understand as macroscopic bodies?

- What parameters are called macroscopic?

- What is the physical meaning of temperature?

- What kind of temperature scales do you know?

- What is the basic equation of the molecular-kinetic theory?

Additional multilevel (on differentiation) tasks

The graph in the figure below shows the best fit line for the results of an experiment in which the volume of a fixed mass of gas was measured over a temperature range from 20°C to 100°C. The pressure of the gas remained constant throughout the experiment.

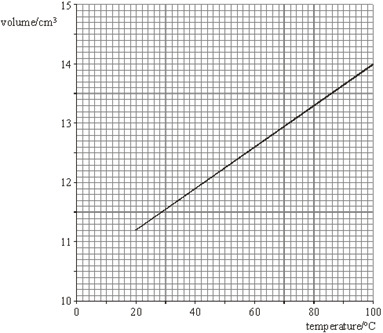
(a)     Use the graph in the figure to calculate a value for the absolute zero of temperature in °C. Show clearly your method of working.  (4)

(b)     Use data from the graph in the figure to calculate the mass of gas used in the experiment. You may assume that the gas behaved like an ideal gas throughout the experiment.

         gas pressure throughout the experiment      =       1.0 × 10⁵ Pa

         molar gas constant                                        =       8.3 J mol^–1 K^–1

            molar mass of the gas used                          =       0.044 kg mol^–1                               (5)

Mark scheme

(a)     m = gradient = 0.035  0.001 (cm² °C⁻¹) B1

          c = intercept = 10.5  0.1 (cm²) B1

          absolute zero = -c/m C1

          = -300  10 °C some relevant working must be seen A1                                 4

or      a meaningful attempt to use similar triangles M1

          an accurate value for the base found C1

          adjustment to the base (if appropriate) C1

          answer = -300  10 °C A1                                                                               4

or      relevant use of V₁/T₁ = V₂/ T₂ M1

          valid introduction of unknown temperature A1

          consistent solution of the equation C1

          answer = -300  10 °C C1                                                                               4

(b)     statement of or use of pV = nRT C1

accurate reading from the line C1

Celsius converted to Kelvin (+273 or + answer to part (a)) C1

          n = 4.52 × 10^–4 or 4.11 × 10^–4 or 4.2 × 10^–4 (∆V/∆T) (mol) A1

m = n × 0.044 (m = 4.52 × 0.044 = 2.0 × 10^–5 kg) B1   5                                 [9]

 Useful links and literature

https://physics.info/gas-laws/

https://www.chem.fsu.edu/chemlab/chm1045/gas_laws.html

http://what-when-how.com/physics/gas-laws/

Скачано с www.znanio.ru