PHYS_10_21_V1_TG_Center of mass

Theoretical material

Consider a body consisting of large number of particles whose mass is equal to the total mass of all the particles. When such a body undergoes a translational motion the displacement is produced in each and every particle of the body with respect to their original position.

If this body is executing motion under the effect of some external forces acting on it then it has been found that there is a point in the system , where whole mass of the system is supposed to be concentrated. The nature the motion executed by the system remains unaltered when force acting on the system is directly applied to this point. Such a point of the system is called center of mass of the system.

Hence for any system Center of mass is the point where whole mass of the system can be supposed to be concentrated and motion of the system can be defined in terms of the center of mass.

The center of mass of a body i a point where whole mass of a body may be assumed to be concentrated for describing its translational motion. On the other hand the center of gravity is the point at which the resultant of the gravitational forces on all the particles of the body acts.

Please note that for many objects, these two points are in exactly the same place. But they're only the same when the gravitational field is uniform across an object. For example in uniform gravitational field such as that of the earth on a small body , the center of gravity coincides with the center of mass.

From above equation we can see that the position vector of a system of particles is the weighted average of the position vectors of the particles of which the system is made up of. Each particle in the system makes contribution proportional to its mass.

Additional problems and tasks

Question 1 Is center of mass a hypothetical point or it really exists?

Answer The concept of center of mass of a system enable us to discuss overall motion of the system. It is defined as a point at which the entire mass of the bodies is supposed to be concentrated. So it is a hypothetical point only. So it is not necessary that the total mass of the system is to be exactly present at the center of mass. Hence we can say that it is a hypothetical point.

Question 2 How is the center of mass depends on the relative distance between the particles?

Answer Consider we have to find out the center of mass of the two masses having mass m Kg and 5m Kg. Now center of mass will lie closer to the heavier body (5m Kg) because center of mass is a point about which the whole mass of the system is balanced.

Question 3 Write two factors on which center of mass of a body does not depend.

Answer density, velocity

Question 4 Give the location of a center of mass of a ring? does it it lie inside the body?

Answer The center of mass of the ring lies in the center of the circle outlined by the ring. It is at the middle of the ring and does not lie inside the body. This is because, center of mass is a mathematical point where the mass of a body seems to be concentrated at.

Question 5 Define motion of center of mass of a fire cracker that explode in air before and after exposition"?

Answer A fire cracker that explodes in air, in the absence of air drag , the center of mass of the fragments would continue to follow the original parabolic path, until the fragmented parts began to touch the ground.

Homework problems’ solutions

1)      This problem is done very easily using equation 2 with two points: the man and woman. Each point has a mass and position, and it is merely a matter of defining the position in terms of some arbitrary origin, and inputting the values into equation 2. This will output an x position relative to the origin that has been decided on.

In the case of this solution I will use the woman as the origin.

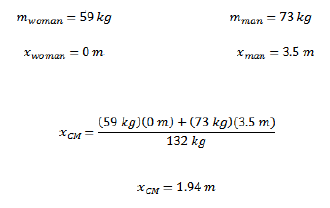
2)      This problem is far more complex than the previous problem and will involve equation 1. We need to begin by defining terms in the equation in terms of values that we are given. To begin with, the problem should be set up like example 6 in the Chapter 10 of the Ohanian Physics book, so that the cone has the y axis point downward from the vertex. We can then define the radius of the cone in terms of its distance in the y direction using the angle we are given. We can define the cone in terms of circular slabs emanating downward from the tip with a thickness of dy and a mass of dm. dm can be defined in terms of y and dy with substitution and using ρ as the density. Once all the terms are defined, the integral can be taken from y=0 to y=h.

3)      This problem is very simple to solve because friction is ignored. This means there are no external forces, so the center of mass of the system (the shark and boat) does not move at all. With this knowledge, it is a simple matter of defining the terms of equation two and then solving for the mass of the shark. The best point to use as an origin in a problem like this is the center of mass, because it will not be moving. Both the shark and the boat will end with their positions on the center of mass.