PHYSICS_10_19_V2_TG_Ohm's law for a mixed connection of conductors.

Review. Complete the sentences (in pairs)

In a parallel circuit, certain general rules may be stated with regard to quantities of voltage, current, resistance, and power. Express these rules, using your own words:

Answers

“In a series circuit, voltage add to equal the total”

“In a series circuit, current is equal across all components”

“In a series circuit, resistance add to equal the total”

“In a parallel circuit, voltage is equal across all components.”

“In a parallel circuit, currents add to equal the total.”

“In a parallel circuit, resistances diminish to equal the total.”

Activity

Identify which of these circuits is a parallel circuit (there may be more than one shown!):

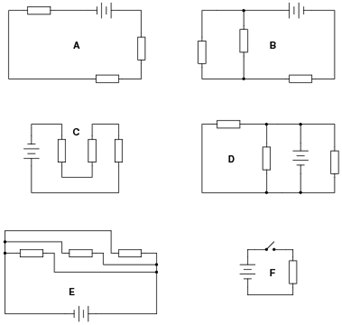
Circuits D and E are parallel circuits.

Notes: 

The purpose of this question is to get students to identify what distinguishing characteristic uniquely identifies a circuit as being “parallel.” Once this has been identified, there are several conclusions which may be deduced (regarding voltage drops, currents, resistances, etc.).

Some students may have difficulty distinguishing that circuit E is a parallel circuit, but it is!

(W) Whole class work. Using Ohm's law for a mixed connection of сonductors

Remember the rules for current and voltage in series and parallel circuits

(G) Group work. Worksheet: Circuits & Ohm’s Law

For further practice analyzing combination circuits, consider analyzing the problems in this activity.

For able students (Differentiation)

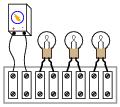
Draw the connecting wires on this terminal strip so that the three light bulbs are wired in parallel with each other and with the battery.

Notes: 

One of the more difficult visualization tasks for new students of electronics is translating schematic diagrams to physical layouts, and visa-versa. This, sadly, is a skill that I don’t see emphasized nearly enough in most basic electronics curricula. It seems the majority of class time is spent mathematically analyzing useless resistor networks, and not enough time is invested building students’ spatial relations skills.

While series connections are very easy to visualize on terminal strips, parallel connections are more difficult. Work with your students through this question helping those who lack the innate spatial relations ability to see the solution quickly.

A “trick” I often use to help students build this skill is to have them first draw a nice, clean schematic diagram. Then they over-trace each wire in the diagram as they draw it in the pictorial diagram. In this way, they make sure not to overlook connections in the pictorial diagram.

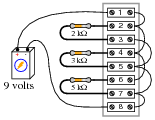
The circuit shown here is commonly referred to as a current divider. Calculate the voltage dropped across each resistor, the current drawn by each resistor, and the total amount of electrical resistance ßeen” by the 9-volt battery:

• Current through the 2 kΩ resistor =

• Current through the 3 kΩ resistor =

• Current through the 5 kΩ resistor =

• Voltage across each resistor =

• R_total =

Can you think of any practical applications for a circuit such as this?

Answer

• Current through the 2 kΩ resistor = 4.5 mA

• Current through the 3 kΩ resistor = 3 mA

• Current through the 5 kΩ resistor = 1.8 mA

• Voltage across each resistor = 9 volts

• R_total = 967.74 Ω

How much current is drawn from the battery in this circuit? How does this figure relate to the individual resistor currents, and to the total resistance value?

Notes: 

Some students may find the diagram hard to follow, and so they will find the task of analysis helped by drawing an equivalent schematic diagram for this circuit, with all terminal points labeled. I recommend you not suggest this solution immediately, but rather challenge your students to think of problem-solving techniques on their own. Surely, someone in the class will have thought of doing this, and the impact of such a suggestion coming from a peer is greater than if it came from you, the instructor.

Be sure to ask your students this question: “Why is this type of circuit commonly called a current divider?”

(f) Formative assessment. Solving problem

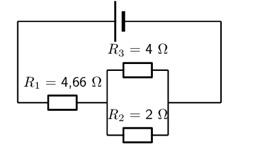
1. If current flowing through the cell is 2 A, and all the resistors are ohmic, calculate the voltage across the cell and each of the resistors, R₁, R₂, and R₃  respectively.

Answer

To find the voltage we first need to find the equivalent resistance. We start by calculating the equivalent resistance of the parallel combination:

1/Rp=1/R₂+1/R₃=1/2+1/4=3/4=1,33 Ω

R_p=1,33 Ω

Now we have a circuit with two resistors in series so we can calculate the equivalent resistance:

Rs=R₁+Rp=4,66+1,33=5,99 Ω

So the voltage across the cell is:

V=I⋅R=(2)(5,99)=12 V

The current through the parallel combination of resistors is 2 A. (The current is the same through series combinations of resistors and we can consider the entire parallel set of resistors as one series resistor.)

Using this we can find the voltage through the each of the resistors. We start by finding the voltage across R₁:

V=I⋅R=(2)(4,66)=9,32 V

Now we find the voltage across the parallel combination:

V=I⋅R=(2)(1,33)=2,66 V

Since the voltage across each resistor in the parallel combination is the same, this is also the voltage across resistors R₂ and  R₃.

2. Complete the table of values for this circuit:

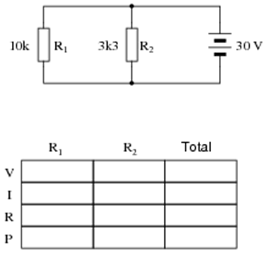
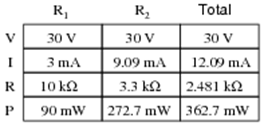
                                                                                              Answer

Notes: 

Discuss with your students what a good procedure might be for calculating the unknown values in this problem, and also how they might check their work.

3. Examine the circuit below:

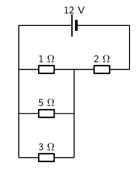
If the potential difference across the cell is 12V, calculate:

·         the current I through the cell.

To find the current I we first need to find the equivalent resistance. We start by calculating the equivalent resistance of the parallel combination:

1/ R_p=1/R₁+1/R₂+1/R₃=1/3+1/5+1/1=23/15

R_p =0,652 Ω

Now we have a circuit with two resistors in series so we can calculate the equivalent resistance:

Rs=R₄+R_p=2+0,652=2,652 Ω

So the current through the cell is:

I=V/R=122,652=4,52 A the current through the 5 Ω resistor.

Answer

The current through the parallel combination of resistors is 4,52 A. (The current is the same through series combinations of resistors and we can consider the entire parallel set of resistors as one series resistor.)

Using this we can find the voltage through the parallel combination of resistors (remember to use the equivalent parallel resistance and not the equivalent resistance of the circuit):

V=I⋅R=(4,52)(0,652)=2,95 V

Since the voltage across each resistor in the parallel combination is the same, this is also the voltage across the 5 Ω resistor.

So now we can calculate the current through the resistor:

I=V/R=2,955=0,59 A

Скачано с www.znanio.ru