МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ

ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ им. В.И.

Вернадского»

(ФГАОУ ВО «КФУ им. В.И. Вернадского»)

Техникум гидромелиорации и механизации сельского хозяйства

(филиал) ФГАОУ ВО «КФУ им. В.И. ВЕРНАДСКОГО» в пгт Советский

ПЛАН-КОНСПЕКТ УЧЕБНОГО ЗАНЯТИЯ

по дисциплине ОП. 02. «Техническая механика» раздел «Сопротивление материалов» тема «Растяжение-сжатие»

Специальность 35.02.07. Механизация сельского хозяйства Группа М-24

Преподаватель                      Ященко Сергей Владимирович

Цели занятия

1.   Дидактическая: дать основы определения продольной силы, определение нормальных напряжений, расчета тел на прочность при растяжении – сжатии.

2.   Воспитательная: прививать студентам аккуратность и четкость

при выполнении схем и эпюр, внимательность при выполнении расчетов, добиваться активности и высокой работоспособности студентов на уроке.

3.   Развивающая: формировать навыки и умения при решении задач, логическое и инженерное мышление.

Уметь: определять напряжения в конструкционных элементах при растяжении сжатии; производить расчеты элементов конструкций на прочность при растяжении сжатии; 

Знать: методику расчета элементов конструкций на прочность при растяжении-сжатии.

Методы обучения используемые при проведении занятия: словесный, практический,  наглядный.

На занятии используются средства ИКТ.

Ход занятия

1.  Организационная часть – 2 минуты

1.1        Проверка подготовленности аудитории к занятию.

1.2        Проверка наличия обучающихся.

2.  Опрос по пройденному материалу – 30 минут.

2.1        Технический диктант.

2.2        Индивидуальный программированный безмашинный опрос по карточкам.

3.Обобщение материала и оценка его усвоения – 3 минуты.

4.     Сообщение нового материала – 25 минут.

5.     Закрепление материала в форме решения задач – 25 минут.

6.     Заключительная часть: подведение итогов. -5минут.

7.     Задание на дом.

Растяжение – сжатие

1. Растяжение – сжатие

Растяжением и сжатием называют вид нагружения, при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – продольная сила N.

Этот вид нагружения также иногда называют осевым или центральным растяжением-сжатием.

Брус при этом называется стержнем.

Для возникновения данного вида деформации линии действия внешних сил или их равнодействующей должны совпадать с осью стержня, проходящей через центры тяжести его сечений.

2. Внутренняя продольная сила

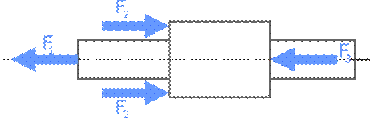
Для расчета внутренних сил по участкам стержня применяется метод сечений.

Величина и знак внутренней продольной силы определяются как сумма всех внешних сил приложенных к рассматриваемой части стержня.

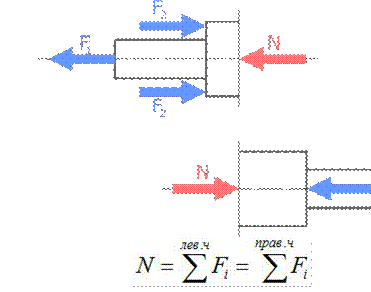
Правило знаков при растяжении и сжатии: внутренняя продольная сила N принимается положительной, если она стремится растянуть рассматриваемую часть стержня. Сжимающая внутренняя сила считается соответственно отрицательной.

                         Для     визуального     представления     распределения     внутренних

продольных сил по длине бруса строятся их эпюры.

3. Напряжения при растяжении и сжатии

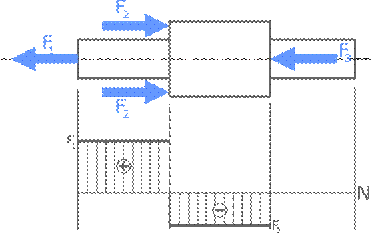
В поперечных сечениях при растяжении-сжатии имеют место только нормальные напряжения σ, которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.

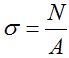
Знак напряжений зависит от знака внутренней продольной силы на рассматриваемом участке стержня.

Опытным путем показано, что при растяжении-сжатии, на достаточном удалении от точки приложения сил, вследствие равномерного распределения внутренних сил по сечению стержня в каждой его точке возникают напряжения одинаковой величины (σ=const).

Для обеспечения необходимой прочности элементов и конструкций

напряжения не должны превышать допустимых значений.

В наклонных сечения бруса одновременно с изменением величины

нормальных напряжений появляются касательные.

4. Центральное (осевое) растяжение-сжатие

Осевым растяжением (сжатием) брусьев называют такой вид деформирования, при котором в их поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N.

Для определения продольной силы используется метод сечений (Рис.

4.1,б).

5. Напряжения

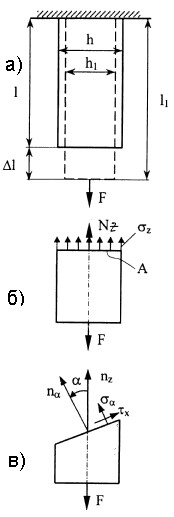
N_z равномерно распределяется по площади поперечного сечения стержня, вызывая нормальные напряжения.

В наклонном сечении возникают нормальные σ_α и касательные τ_α напряжения

(рис. 4.1,в).

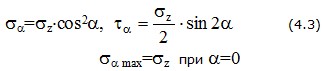
причем

6. Деформации

При осевом растяжении (сжатии) наблюдаются абсолютные и относительные деформации (рис. 4.1,а):

l₁    –    l    =    Δl    -    абсолютная    продольная    деформация    (удлинение);

h₁ – h = -Δh - абсолютная поперечная деформация (сужение); относительная продольная деформация:

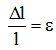
относительная поперечная деформация:

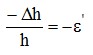
Отношение

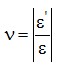
называется     коэффициентом    поперечной     деформации    (коэффициентом

Пуассона).

Напряжения        и        деформации        взаимосвязаны        законом        Гука

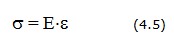
где Е - модуль упругости (модуль Юнга).

В общем случае удлинение стержня определяется по формуле

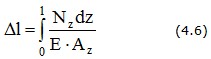
В частном случае, когда жесткость сечения ЕА = const и N_Z= F = const

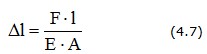
При ступенчатом изменении нагрузки N_z и конфигурации сечения

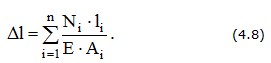
В результате деформации бруса его поперечные сечения получают линейные перемещения U_(z). Так, перемещение сечения В, находящегося на расстоянии z от закрепленного конца, равно удлинению Δl_z части бруса длиной z, заключенной между неподвижным и рассматриваемым сечением.

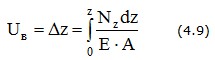
Взаимное перемещение двух сечений В и С бруса равно удлинению части бруса, заключенной между этими сечениями

U_(B-C)=Δl_B-C        (рис.4.2)

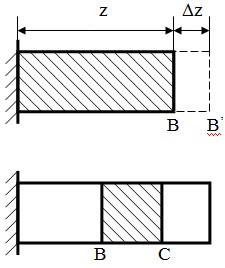
Рис. 4.2

                         Перемещение    точек    стержневой    системы    (BCD)    (Рис.    4.3)

происходит как за счет продольных деформаций (U_СВ =  Δl_BC, U_CD = Δl_DC), так и за счет поворота деформированных стержней BC₁ и DC₂ относительно шарниров (B, D) как твердого тела по дугам С₁С₃ = δ₁ и С₂С₃ = δ₂, замененными перпендикулярами к радиусам поворота (ВС₁ и DС₂).

Отрезок СС₃ = δ_с соответствует полному перемещению узла С в

результате деформации стержней ВС и DС.

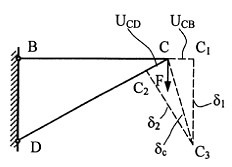
Рис. 4.3

7. Условие прочности

Условие прочности при растяжении (сжатии) выражается неравенством:

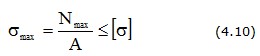
где [σ] – допускаемые напряжения, определяются как:

n – коэффициент запаса прочности, устанавливаемый нормативными документами.

Условие прочности позволяет решать три типа задач:

1.     Проверка        прочности (проверочный      расчет)

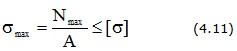
2.     Подбор сечения       (проектировочный        расчет)

3.     Определение   грузоподъемности        (допускаемой      нагрузки)

Условие жесткости

Условие жесткости стержня

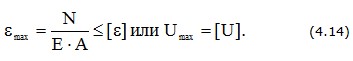
Условие жесткости узла стержневой системы

Потенциальная энергия упругой деформации стержня

Контрольные вопросы

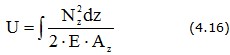
1.       Метод сечений. Внутренние силы в поперечных сечения бруса.

2.       Напряжения.

3.       Силы в поперечных сечениях бруса при растяжении – сжатии.

4.       Напряжения  в поперечных сечениях бруса при растяжении – сжатии.

5.       Деформации и перемещения при растяжении – сжатии.

Домашнее задание  Л3 стр. 24-39

Список использованных источников

1.Аркуша А.И. – Теоритическая механика и сопротивление материалов, учебное пособие. Высшая школа, 2002 г., 354 стр.

2.Никитин Е.М. – Теоретическая механика для техникумов, М. Наука, 1988 г.

3. Ицкович Г.М. – Сопротивление материалов, М, Высшая школа, 1987 г.