Площадь сферы

Урок по теме «Площадь поверхности сферы»

Цели урока:

·                    Образовательные: создать условия для закрепления понятий «сфера», «шар», элементы тела;  познакомить учащихся с формулами нахождения площади поверхности сферы, сформировать умения применять формулы (полученные знания) при решении задач;

·                    Развивающие: Развивать память, логическое мышление, внимание. Развитие интереса к изучению математики;

·                    Воспитательные: воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения.

Ход урока.

1. Организационный момент. Проверка готовности к уроку.

Ход урока:

1. Организационный момент. Мотивация урока.

Приветствие учеников. Сообщение учащимся краткого плана урока. Ребята, работа предстоит большая, поэтому, прошу всех настроиться на серьёзную работу.

Девиз урока: Дорогу осилит идущий, а геометрию – мыслящий. 

2. Актуализация опорных знаний. Проверка домашнего задания.

Ребята, к сегодняшнему уроку я просила повторить вас определение окружности, круга и всех понятий, связанных с ними. Все точки круга и окружности, обладая определённым свойством, лежат в одной плоскости.

Задание 1: Сформулируйте определение окружности  и ее элементов.

Задание 2: Сформулируйте определение круга и его элементов.

Окружность – множество точек плоскости, равноудаленных от данной точки. Данная точка – центр окружности. Радиус – отрезок, соединяющий центр окружности с ее любой точкой. Диаметр – отрезок, соединяющий две точки окружности и проходящий через ее центр. 

Круг – это часть плоскости, ограниченная окружностью. Центр, радиус и диаметр окружности являются центром, радиусом и диаметром круга. 

3. Усвоение  новых знаний.

Сегодня на уроке мы должны с вами обобщить  определения шара, сферы, всех связанных с ними понятий.

 Сформулируйте определение шара (шар-это геометрическое тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки, эта точка называется центром шара, а данное расстояние - радиусом шара). Сформулируйте определение сферы (сфера-это геометрическое тело, которое состоит из всех точек пространства, равноудалённых от данной точки, эта точка называется центром сферы, а данное расстояние - радиусом сферы). Ребята, а ещё сферой или шаровой поверхностью называют границу шара. Шар и сфера являются телами вращения. Попытайтесь сформулировать определение шара и сферы, как тел вращения (шар-это геометрическое тело, которое получается при вращении полукруга или круга вокруг его диаметра как оси; сфера - это геометрическое тело, которое получается при вращении полуокружности или окружности вокруг её диаметра как оси). Слова “шар” и “сфера” происходят от одного и того же греческого слова “сфайра” - мяч.

Рассмотрим определения понятий, связанных с шаром и сферой: радиуса, хорды, диаметра, оси, полюсов, диаметрально противоположных точек, диаметральной плоскости, большого круга, большой окружности.

Решим устно задачу по готовому чертежу:

Доказательство:

Рассмотрим АМО и МВО. Эти треугольники прямоугольные, т.к. ОМ АВ (по условию задачи).

АМО = ВМО. Так как ОМ – общий катет, ОА=ОВ=R – гипотенузы. Значит АМ=МВ.

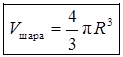
 При решении задач на шар (сферу) чаще всего чертят осевое сечение шара (сферы) - круг, тогда большая окружность изображается диаметром этого круга. Ну, а если хотят сделать рисунок шара или сферы, то чертят круг; центр круга, являющийся центром шара (сферы); большой круг изображают в виде эллипса; чертят полюса, которые чуть-чуть “затапливают”.

4. Зарядка для глаз.

Мы много поработали, глаза устали, давайте отдохнем.

Примером сферы может служить поверхность земного шара. Экватор делит земную поверхность на две полусферы – Северное и Южное полушария.

Нулевой меридиан и меридиан измерения дат делит земную поверхность на Западное и Восточное полушария. И сейчас отправимся в путешествие по полушариям. Сядьте удобнее, расслабьтесь. Каждое задание выполняем по 10 раз.

1.                  Обведите полушария по направлению стрелки.

2.                  Проведите глазами по вертикальной прямой сверху вниз.

3.                  Проведите глазами по горизонтальной прямой справа налево.

4.                  Обведите внутренний овал против часовой стрелке.

5.                  Обведите внешний овал по часовой стрелке.

6.                  Закройте глаза.

Откройте глаза. С новыми силами приступаем к работе.

5. Закрепление нового материала.

Приведите примеры из окружающего нас мира тел, имеющих шарообразную форму. Говорить о значении шара (сферы) в жизни человека можно очень много, и мы будем это делать на последующих уроках. Я хочу только дополнить, что свойства шара и сферы продолжают изучать и в наши дни физики, химики, биологи, астрономы, геодезисты, медики, так как уж очень часто их объекты наблюдения и исследования имеют шарообразную форму. Решение задач учащимися под руководством учителя и с его помощью:

а) Дано: V = 113,04 см³. Найти R и S.

V =πR³,  отсюда,  R³ =,  значит,  R =.

R =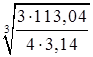≈≈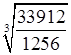≈ 3 (см).

R ≈ 3 см.

S = 4πR² ≈ 4π ∙  3² ≈ 36π (см²).

S ≈ 36π см².

Ответ: ≈ 3 см; ≈ 36π см².

б) Дано: S = 64π (см²). Найти R и V.

S = 4πR²,   отсюда R² =,   то R =;

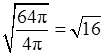R == 4 (см);

R = 4 см.

(см³).

Ответ: 4 см; π см³.

В) Диаметр Луны составляет (приближенно) четвертую часть диаметра Земли, то есть d_Земли = 4d_Луны, тогда радиус земли в 4 раза больше радиуса луны, то есть R₁ = 4R₂. Найдем объем луны

.

Найдем объем земли

.

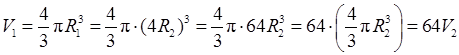Значит, объем земли в 64 раза больше объема луны.

Ответ: в 64 раза.

6. Самостоятельная работа.

Тест по теме  «Сфера и шар»

1. Выберите неверное утверждение.

А) сечение шара плоскостью есть окружность;

Б)  сфера может быть получена в результате вращения полуокружности вокруг её диаметра;

В) тело, ограниченное сферой, называется шаром;

Г)  площадь сферы можно вычислить по формуле S = 4pr2;

2. Какое сечение шара плоскостью имеет наибольшую площадь?

А) Сечение круга   Б)  Сечение, перпендикулярное диаметру шара

В)  Сечение, параллельное диаметру шара

Г)  Сечение, проходящее через точку, которая делит диаметр 3:2.

3. Через всякие ли три точки можно провести сферу?

А) Нет, точки, не должны принадлежать одной прямой Б) Да

В)  Да, если три точки лежат на одной прямой   Г)  Нельзя ответить

4. Сколько общих точек может иметь сфера и прямая?

А)  Две, одну, ни одной     Б) Две         В)  Одну        Г)  Ни одной

5. Сколько общих точек может иметь сфера и плоскость?

А)  Бесконечно много точек, принадлежащих окружности, одну, ни одной

Б)  Одну В)  Ни одной

Г)  Бесконечно много точек, принадлежащих окружности

6. Сколько касательных плоскостей можно провести к данной сфере через прямую, проходящую вне сферы?

А)  Две              Б)  Бесконечно много    В)  Одну     Г)  Ни одной

7. Сколько касательных плоскостей можно провести к данной сфере через точку, проходящую вне сферы?

А)  Бесконечно много      Б) Одну    В) Две     Г) Ни одной

7.                  Назовите элемент, не принадлежащий цилиндру:

А) апофема      Б) высота       В) образующая   Г) радиус

8.                  Осевым сечением цилиндра является:

А) треугольник   Б) круг      В) прямоугольник   Г) трапеция

10. Конус не может быть получен вращением:

А) прямоугольника вокруг одной из сторон;

Б) равностороннего треугольника вокруг медианы;

В) прямоугольного треугольника вокруг одного из катетов;

Г) равнобедренного треугольника вокруг высоты.

11.Назовите элемент, не принадлежащий конусу:

А) образующая    Б) ось    В) высота    Г) медиана

12.Сфера является поверхностью:

А) конуса   Б) усечённого конуса   В) цилиндра   Г) шара

7. Подведение итогов урока. Д/з.

8. Рефлексия.

Ребята, я оценила вашу работу на уроке. Я прошу вас, когда вы будете после урока выходить из класса, оцените каждый самостоятельно свою работу на уроке с помощью соответствующего смайлика на листе бумаги, помещённом на крыле магнитной доски.

Урок окончен, спасибо вам за урок, ребята.

Д/з:_____________