Подготовка к ЕГЭ. Тригонометрические уравнения. Отбор корней

МБОУ « Шлиссельбургская средняя общеобразовательная школа №1 с углубленным изучением отдельных предметов»

Методическая разработка по теме

«Подготовка к ЕГЭ. Тригонометрические уравнения. Отбор корней»

Учитель математики Ламанцева Н.М.

2023 г.

ЕГЭ  профильный уровень

Погружение в математику  Задание № 13

ЕГЭ №13

•       а) Решите уравнение

•       б)  Укажите корни уравнения, принадлежащие данному промежутку

Критерии оценивания

Справочные материалы

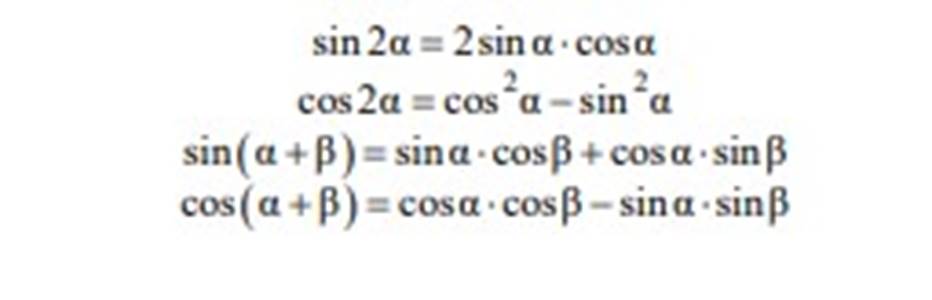
Рекомендации по решению тригонометрических уравнений

•       Найти ограничения

•       Свести уравнение к простейшему

Некоторые методы решения тригонометрических уравнений

•       Применение тригонометрических формул

•       Использование формул сокращённого умножения

•       Разложение на множители

•       Сведение к квадратному уравнению относительно sin x, cos x, tg x

•       Введение вспомогательного аргумента

•       Деление обеих частей однородного уравнения первой степени (asin x +bcosx = 0) на cos x

•       Деление обеих частей однородного уравнения второй степени (a sin² x +bsin x cos x+ c cos²x =0) на cos² x

•      
С помощью тригонометрической окружности

•       С помощью неравенства

ПриведитеСколькоНазовитеКакое пример корней два из  чиселчисла тригономет имеет больше,  уравнениерического уравненияsin xarccos, 0которое ,которых3?0 или  неarcsin равен имеет0  ? .корней3. . косинус

2

                                                                                               3              3сosx

sin x

2

cosxx tg  3

2

3sin x1

№1. а). Решите уравнение     2sin3 x 2sin xcos2 x0

б). Найдите корни этого уравнения, принадлежащие отрезку ³ x 2sin x                             ²                 ^;



                                                                      2sincos x0                       2                                        

2sin x(sin² x1)cos² x0

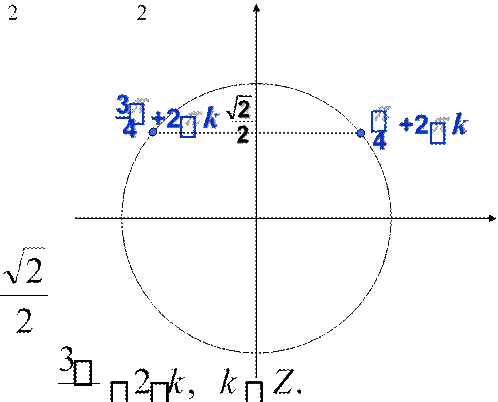2sin x(sin² xsin² xcos x)cos x0

2sin x(cos² x)cos² x0

 2sin xcos² xcos² x0 cos² x( 2sin x1)0

cosx0                         sin x

а). Ответ: ^k; ^2k;

                                                                       2             4                4

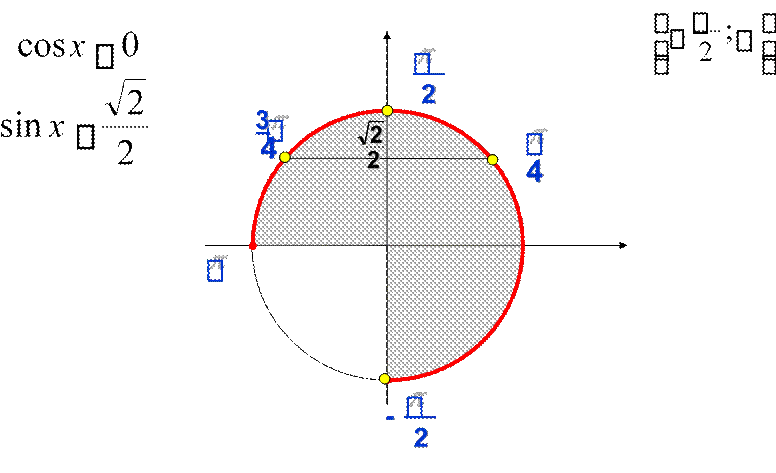
б). Найдите все корни этого уравнения, принадлежащие отрезку

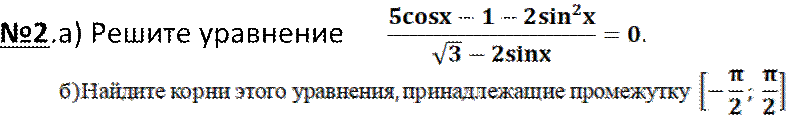
Решение

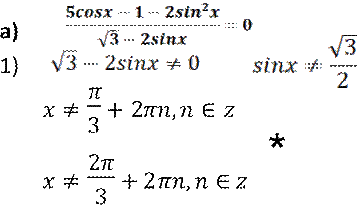
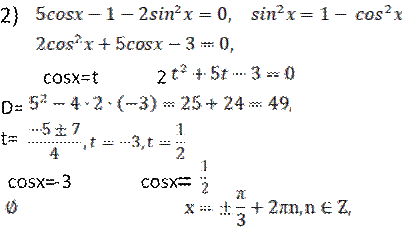                                                           x

б) Отбор корней с помощью тригонометрической окружности: -

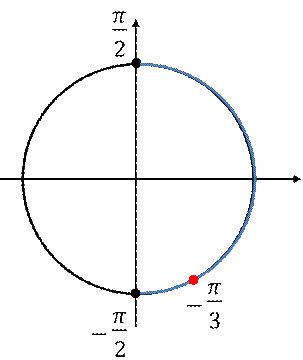
Ответ: а)

№3. а). Решите уравнение  cos2x3sin² x1,25

б). Найдите все корни этого уравнения, принадлежащие отрезку

cos2x3sin² x1,25 ^_;^5_ cos² xsin² x3sin² x1 ^ 2 ^

cos² x2sin² x1

1sin² x2sin² x1

1sin² x1 sin² x

sin x         sin x

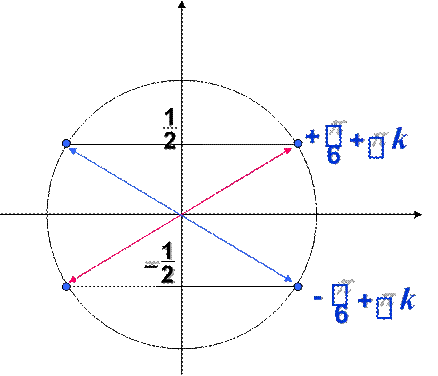
а). Ответ:x^k, kZ 6

б). Найдите все корни этого уравнения, принадлежащие отрезку а). Решите уравнение cos2x3sin2 x1,25                                         ;52

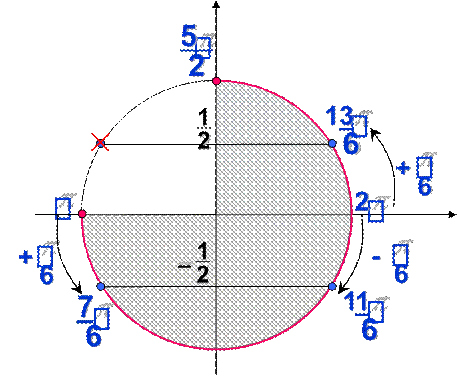
б). Ответ: 7; 11; 13.

                                                                                                                                                                                                                          6       6 6

а) Решите уравнение.

б) Найдите корни уравнения, принадлежащие данному отрезку.

№4.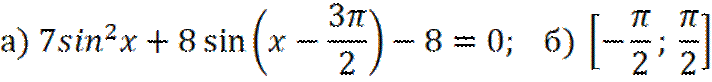

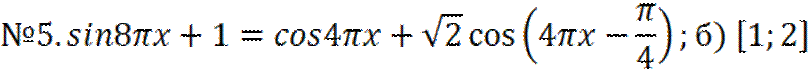
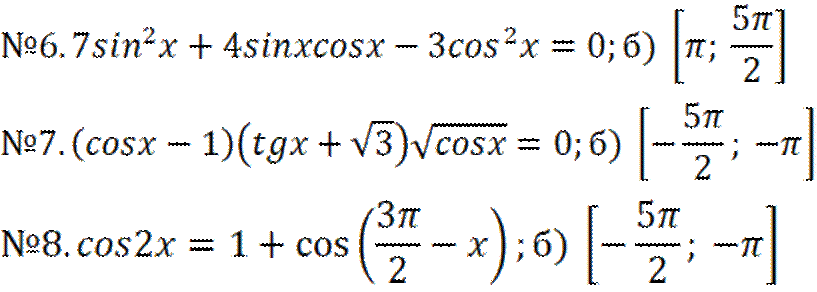
а) Решите уравнение.

б) Найдите корни уравнения, принадлежащие данному отрезку.

№9-№14

(Приложение)

№15 (дополнительное задание)

Укажите количество корней уравнения

cosх  2 c x _

cosx

при всех значениях параметра с.