Поделиться
Повт.Подг.к ГВЭ.треуг..docx
Треугольники и их элементы.
Рассмотрим решение задач.
Задача 1. В треугольнике 
, 
. Найдите 
.
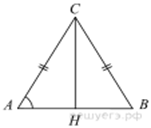Решение.
Треугольник 
равнобедренный,
значит, высота 
делит основание 
пополам,
поэтому
.
По определению
.
Ответ: 0,6.
Самостоятельно.
1.
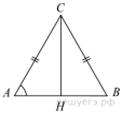
, высота 
равна 20. Найдите 
.
2. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
3. В треугольнике 
. Внешний угол при вершине 
равен 
. Найдите угол 
.
Ответ дайте в градусах.
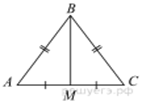
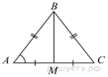
4. В треугольнике ABC
известно, что AB = BC = 13, AC = 10 . Найдите длину
медианы BM.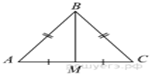 
Задача 2. В треугольнике 
угол 
равен
Найдите
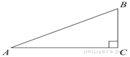
Решение.
Зная, что 
а 
по определению косинуса имеем:
Тогда по теореме Пифагора
Ответ: 6.
Самостоятельно.
5.
В треугольнике ABC угол С
равен 90°, АВ = 4, ВС = 2. Найдите 
.
6. Катеты прямоугольного треугольника равны 6 и 8. Найдите наибольшую среднюю линию треугольника.
7.
В треугольнике 
угол
равен
. Найдите 
.
8.
В треугольнике 
, 
. Найдите длину медианы 
.
Задача 3. В треугольнике 
угол 
равен 
, 
. Внешний угол при вершине 
равен
. Найдите 
.
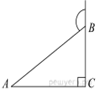
Решение.
Внутренний ∠B = 180 − 120 = 60°, ∠А = 180 − 60 − 90 = 30°. Против угла в 30° лежит катет равный половине гипотенузы. Следовательно, BC = 6.
Ответ: 6.
Самостоятельно.
9. В треугольнике 
, внешний угол при
вершине 
равен
. Найдите 
.
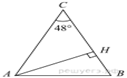
10. В равнобедренном треугольнике ABC с основанием AB угол С равен 48°. Найдите угол между стороной AB и высотой АН этого треугольника.
11. В равнобедренном треугольнике ABC основание AC = 28,
Найдите площадь треугольника ABC.
12 .В прямоугольном треугольнике ABC угол C равен
90°, 
Найдите площадь треугольника ABC.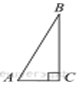 
Ответы на задачи.
|
№1 |
0,6 |
|
№2 |
12 |
|
№3 |
64 |
|
№4 |
12 |
|
№5 |
0,5 |
|
№6 |
5 |
|
№7 |
0,6 |
|
№8 |
24 |
|
№9 |
7 |
|
№10 |
24 |
|
№11 |
280 |
|
№12 |
1320 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
