а) Решите уравнение sin2 x3cosx30.

 3;^.

б) Найдите все корни уравнения, принадлежащие промежутку ^

_ 2 2_

Решение:

а)

sin² x3cosx30 

1cos² x3cosx30 sin² x 1cos² x

cos² x3cosx40  cos² x3cosx40 

Пусть cos x  t, где 1 t 1, тогда  t² 3t 40  t₁ 1; t₂ 4не удовлетворяет условию1t 1 

Вернемся к замене  cosx1  x 2k,kZ 

^ 32;2^.

б) Найдем корни уравнения, принадлежащие промежутку 

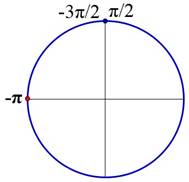                                                                                                    корень      данного      уравнения,

^ 32;2. принадлежащий промежутку 

Ответ: а) 2k,kZ ; б) .

а) Решите уравнение sin2 x3sin2x7cos2 x 0.

 ;^.

б) Найдите все корни уравнения, принадлежащие промежутку 

 2 2

Решение:

а) 

sin² x3sin2x7cos² x 0 sin2x 2sin xcos x

sin² x6sinxcosx7cos² x 0 :cos² x tg²x 6tgx 7  0 

Пусть tg x  t, тогда  t² 6t 7  0  t₁ 1; t₂ 7 

Вернемся к замене  tg x 1 или tg x 7  x  ^ k,kZ x  arctg7n,nZ  

4

 ;.

б) Найдем корни уравнения, принадлежащие промежутку 

 2 2

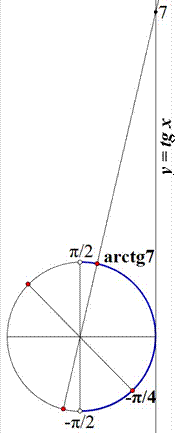
/ 4 и arctg 7  корни данного уравнения,

 ;.

принадлежащие промежутку 

 2 2



Ответ: а)   k,k Z; arctg7n,nZ ; ⁴

                                                                                  б) / 4, arctg 7.

а) Решите уравнение 2sin2 x sinx10.

                                                                                                                                                                      ;32^_.

б) Найдите все корни уравнения, принадлежащие промежутку 

Решение:

а) 

2sin² x sinx10                                                                  

Пусть sin x  t, где 1 t 1, тогда                                 

2t² t 10          t₁ 1; t₂         

Вернемся к замене      sinx 1  или   sinx       

x  2m,mZ     6

б) Найдем корни уравнения, принадлежащие промежутку ^;32^_.

3^

1) Выясним, для каких целых k выполняется неравенство  x      :

2

                                                 3

                  2k                        2

                                      2                 2

24k 3 

4k 4 : 4

   k 1          kZ  k 0;1 

2)    Найдем значения x:

при k  0 x  ^  2k  ^  20  ^;

                                                             2                   2                     2

   при k 1 x  ^  2k  ^  21 3^                                 

                                                            2                   2                   2

3)    Выясним, для каких целых n из серии x ^  2n,nZ выполняется

6 3^

неравенство  x  :

2

                                            3^

                  2n                           6

                                 6                 2

612n 9 

712n8 :12

 n            nZ  n  0 

4)    Найдем значение x при n 0:

x   ^  2n ^  20 ^

6                                       6 6

5^

5)    Выясним, для каких целых m из серии x         2m,mZ

6

3^

выполняется неравенство  x :

5   3^    2m          6

                                  6                   2

6512m 9 5

                1112m 4                              :12

 m 

mZ  m  0

6)    Найдем значение x при m  0:

x    5 2m  5 20  5

6                                       6 6   5^

Ответ: а)    2k,k Z;     2n,nZ;    2m,mZ;;

                                    2                           6                           6

 5 3

             б)     ;     ;       ;       .                                       

2 6 6 2

Пример 4

а) Решите уравнение 3cos4x 2sin2 4x.

 4 ^;32_.

б) Найдите все корни уравнения, принадлежащие промежутку 

Решение:

а) 

3cos4x 2sin² 4x 

3cos4x  21cos² 4x sin² 4x 1cos² 4x

3cos4x 22cos² 4x 

2cos² 4x3cos4x20 

Пусть cos4x  t, где 1 t 1, тогда 

2t² 3t 20 

t₁ ; t₂ 2не удовл. условию 1 t 1

Вернемся к замене 

1

cos4x  2

4x  ^ 2k,kZ                                                     

3

x    k ,k Z 

12 2

б) Найдем корни уравнения, принадлежащие промежутку ^^4 ;32^_.

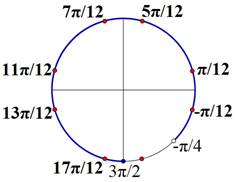
 5 7 11 13 17

                                                                                                             ;        ;      ;        ;        ;         

12 12 12 12 12 12

корни данного уравнения, принадлежащие  промежутку 4 ;32.

Ответ: а)   k ,k Z ; б)   ;5;7;11;13;17.

                                      12 2                                 12 12 12 12 12 12

Пример 5

а) Решите уравнение sin2 x3sinxcosx2cos2 x 0.

б) Найдите все корни уравнения, принадлежащие промежутку 2 ;^4^_ .

Решение:

а) 

sin² x3sinxcosx2cos² x 0 :cos² x tg²x 3tg x  2  0  Пусть tg x  t, тогда  t² 3t  2  0  t₁ 1; t₂ 2 

Вернемся к замене  tg x 1 или tg x 2 

x ^k,kZ               x  arctg2n,nZ               

4

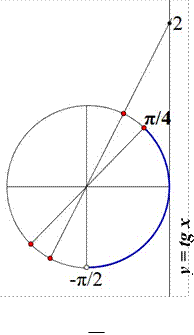
б) Найдем корни уравнения, принадлежащие промежутку ^^2 ;^4^_ .

/ 4  корень данного уравнения, принадлежащий промежутку ^^2 ;^4^_ .



Ответ: а)         k,k Z; arctg2n,nZ ;  б) / 4.

4