Добавить материал

и получить 10 документов
и свидетельство СМИ

Полиёва Елена Ивановна

Подготовка к ОГЭ. Теория по теме "Прямоугольный треугольник"

Подготовка к тестированию
docx
11.02.2017

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

В помощь для подготовки к ОГЭ: треугольник, виды треугольников, основные линии в треугольнике, соотношения между сторонами и углами треугольника, признаки равенства и подобия треугольников, равнобедренный треугольник, равносторонний треугольник, свойства и признаки равнобедренного треугольника, формулы для вычисления площади треугольника, формулы для вычисления элементов равностороннего треугольника.

Прямоугольный треугольник.docx

Прямоугольный треугольник

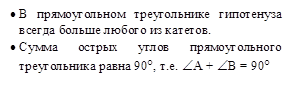
• В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
• Сумма острых углов прямоугольного треугольника равна 90°, т.е. ÐА + ÐВ = 90° Треугольник назыается прямугольным, если один из его углов - прямой, то есть равен 90°.

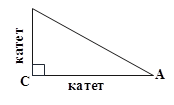Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.

или

Признаки равенства прямоугольных треугольников

Признаки подобия прямоугольных треугольников

· По двум катетам

· По катету и гипотенузу

· По катету и прилежащему острому углу

· По катету и противолежащему острому углу

· По гипотенузе и острому углу

· По одному острому углу

· По пропрциональности двух катетов

· По пропорциональности катета и гипотенузы

Частные случаи прямоугольных треугольников

Свойства проекций катетов
	Высота – среднее пропорциональное м/у проекциями катетов на гипотенузу		Каждый катет – среднее пропорциональное м/у гипотенузой и проекцией этого катета на гипотенузу	– высота ч/з стороны – высота ч/з проекции катетов
Соотношения в прямоугольном треугольнике
		Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе.
		Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.
		Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.

Медиана, проведенная из вершины прямог угла, равна половине гипотенузы

· Центр описанной окружности совпадает с серединой гипотенузы (точка О).

· Радиус описанной кружности:

Радиус вписанной в прямоугольный треугольник окружности:

Прямоугольный треугольник Треугольник назыается прямугольным, если один из его углов - прямой, то есть равен 90 °

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также