МЕТОДИЧЕСКАЯ РАЗРАБОТКА

По дисциплине: «Информатика»

Методические рекомендации по теме:

«Подходы к понятию информации и измерению информации»

2019 г

Пояснительная записка

Данная методическая разработка предназначена для студентов любой формы обучения по предмету: Информатика. Может использована педагогами для проведения уроков по данной теме, для организации самостоятельной работы обучающихся.

Учебно-методическая разработка содержит весь необходимый материал для проведения уроков информатики по теме “Подходы к понятию информации и измерению информации”: теоретический материал, разбор решения типовых задач, задания для самостоятельного изучения и закрепления новых знаний и умений. 

Цель методической разработки: закрепление навыков решения заданий по информатике с использованием приемов и методов измерения количества информации: алфавитного и вероятностного.

Подходы к понятию информации и измерению информации

Информатика - это наука об организации процессов получения, хранения, обработки и передачи информации в системах различной природы. Информатика также изучает возможность автоматизации информационных процессов компьютерными средствами. Синонимом слова "компьютер" является "электронно-вычислительная машина" или ЭВМ. Персональный компьютер - один из видов компьютеров наряду с многопроцессорными и мультисистемными компьютерами. Сущность же компьютера - это транзисторная технология, которая реализована во всей современной радиотехнике. Более того, процессор как основа компьютера также не является уникальным явлением, так как процессоры сегодня могут иметь как телефоны, телевизоры, так и другие бытовые устройства.

Информация (в переводе с латинского informatio - разъяснение, изложение) - это ключевое понятие современной науки, которое стоит в одном ряду с такими как "вещество" и "энергия". Существует три основные интерпретации понятия "информация".

Научная интерпретация. Информация - исходная общенаучная категория, отражающая структуру материи и способы ее познания, несводимая к другим, более простым понятиям.

Абстрактная интерпретация. Информация - некоторая последовательность символов, которые несут как вместе, так в отдельности некоторую смысловую нагрузку для исполнителя.

Конкретная интерпретация. В данной плоскости рассматриваются конкретные исполнители с учетом специфики их систем команд и семантики языка. Так, например, для машины информация - нули и единицы; для человека - звуки, образы, и т.п.

Существуют несколько концепций (теорий) информации.

Первая концепция (концепция К. Шеннона), отражая количественно-информационный подход, определяет информацию как меру неопределенности (энтропию) события. Количество информации в том или ином случае зависит от вероятности его получения: чем более вероятным является сообщение, тем меньше информации содержится в нем.

Вторая концепция рассматривает информацию как свойство (атрибут) материи. Ее появление связано с развитием кибернетики и основано на утверждении, что информацию содержат любые сообщения, воспринимаемые человеком или приборами. Наиболее ярко и образно эта концепция информации выражена академиком В.М. Глушковым.

Третья концепция основана на логико-семантическом (семантика - изучение текста с точки зрения смысла) подходе, при котором информация трактуется как знание, причем не любое знание, а та его часть, которая используется для ориентировки, для активного действия, для управления и самоуправления. Иными словами, информация - это действующая, полезная, "работающая" часть знаний. Представитель этой концепции В.Г. Афанасьев.

В настоящее время термин информация имеет глубокий и многогранный смысл. Во многом, оставаясь интуитивным, он получает разные смысловые наполнения в разных отраслях человеческой деятельности:

·                   в житейском аспекте под информацией понимают сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специальными устройствами;

·                   в технике под информацией понимают сообщения, передаваемые в форме знаков или сигналов;

·                   в теории информации (по К.Шеннону) важны не любые сведения, а лишь те, которые снимают полностью или уменьшают существующую неопределенность;

·                   в кибернетике, по определению Н. Винера, информация - эта та часть знаний, которая используется для ориентирования, активного действия, управления, т.е. в целях сохранения, совершенствования, развития системы;

·                   в семантической теории (смысл сообщения) - это сведения, обладающие новизной, и так далее...

Такое разнообразие подходов не случайность, а следствие того, что выявилась необходимость осознанной организации процессов движения и обработки того, что имеет общее название - информация.

Информация и знания. Человек получает информацию из окружающего мира с помощью органов чувств, анализирует ее и выявляет существенные закономерности с помощью мышления, хранит полученную информацию в памяти. Процесс систематического научного познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и т.д.).

Т.о., с точки зрения процесса познания информация может рассматриваться как знания.  Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.

Уменьшение неопределенности знаний. Подход к информации как мере уменьшения неопределенности знаний позволяет количественно измерять информацию, что чрезвычайно важно для информатики. Рассмотрим вопрос об определении количества информации более подробно на конкретных примерах.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий – монета окажется в одном из 2-х положений: «орел» или «решка».

Можно говорить, что события равновероятны, если при возрастающем числе опытов количества выпадений «орла» и «решки» постепенно сближаются. Например, если бросить монету 10 раз, то «орел» может выпасть 7 раз, «решка» - 3 раза. Если бросить монету 100 раз, то «орел» может выпасть 60 раз, «решка» - 40. Если бросить 1000 раз, то «орел» может выпасть 520 раз, «решка» - 480 и т.д. В итоге при очень большой серии опытов количество выпадений «орла» и «решки» практически сравняются.

Перед броском существует неопределенность наших знаний (возможны 2 события), и как упадет монета, предсказать невозможно. После броска наступает полная определенность, т.к. мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении (например, «орел»). Это сообщение приводит к уменьшению неопределенности наших знаний в 2 раза, т.к. до броска мы имеем два вероятных события, а после броска – только одно, т.е. в два раз меньше.

В окружающей действительности достаточно часто встречаются ситуации, когда может произойти некоторое количество равновероятных событий. Так, при бросании равносторонней четырехгранной пирамиды существует 4 равновероятных события, а при бросании шестигранного игрального кубика – 6 равновероятных событий.

Единицы измерения количества информации. Для количественного выражения любой величины необходимо определить единицу измерения. За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность в 2 раза. Такая единица названа «бит». Если вернуться к опыту с бросанием монеты, то здесь неопределенность как раз уменьшается в 2 раза и следовательно полученное количество информации равно 1 биту.

Например, 1 бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет и т.д.

В информатике принято рассматривать последовательности длиной 8 бит. Такая последовательность называется байтом.

1 байт = 8 бит.

1 Кб=1024 байта=2¹⁰ байта.

1Мб=1024 Кб=2²⁰ байта.

1Гб=1024 Мб=2³⁰ байта.

1Тб=1024 Гб=2⁴⁰ байта.

Методы измерения количества информации: вероятностный и алфавитный.

Единицей измерения количества информации является бит. 1 бит – количество информации, содержащейся в сообщении, которое в двое уменьшает неопределенность знаний о чем либо. Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли: N=2^I.

Например, пусть шарик находится в одной из 4-х коробок. Т.о, имеется 4 равновероятных события (N=4). Тогда по формуле Хартли 4=2^I , I=2.Т.е., сообщение о том, в какой именно коробке находится шарик, содержит 2 бита информации.

N=2^I

N – количество независимых кодируемых значений.

I – разрядность двоичного кодирования.

Алфавитный подход.

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятны, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:

Например, в русском языке 32 буквы (буква ё обычно не используется), т.е. количество событий будет равно 32. Тогда информационный объем 1-го символа будет равен: битов.

Если N не является целой степенью 2, то число  не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как , где  - ближайшая к N степень двойки, такая, что .

Например, в английском языке 26 букв. Информационный объем 1-го символа можно найти так: битов.

Если количество символов алфавита равно N, а количество символов в записи сообщения равно M, то информационный объем данного сообщения вычисляется по формуле: .

Задача № 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из 2-х состояний («вкл» или «выкл»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение: С помощью N лампочек, каждая из которых может находиться в одном из 2-х состояний, можно закодировать 2^N сигналов. пяти лампочек недостаточно, а 6 хватит.

Ответ. 6 лампочек.

Задача № 2. Метереологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

Решение: В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения  . Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128=2⁷. Принимаем для одного измерения битов. Для 80 измерений общий информационный объем равен: 80*7=560 битов=70 байтов.

Ответ. 70 байтов.

Вероятностный подход.

Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятностные реализации.

В этом случае количество информации определяют по формуле Шеннона:

,

где I – количество информации

      N – количество возможных событий

      P_i – вероятность i-го события.

Например, пусть при бросании несимметричной четырехгранной пирамиды вероятности отдельных событий будут равны: .

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

бита.

Скорость передачи информации и пропускная способность канала связи.

Прием (передача) информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока.

Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с., а также в байт/с, Кбайт/с, Мбайт/с.

Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.

Пример: Скорость передачи данных через ADSL – соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.

Решение: Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3*60 = 180 с.

Выразим скорость в Кбайт/с: 256000 бит/с = (256000:8:1024) Кбайт/с.

Размер файла = (256000:8:1024) * (3*60) = 5625 Кбайт.  

Задачи для решения

Задача 1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25 красных, 25 синих шариков. Для этого необходимо использовать следующую формулу 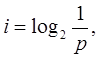 где i - это количество информации, р - вероятность события.

Вероятность события выражается в долях единицы и вычисляется по формуле:  где К — величина, показывающая, сколько раз произошло интересующее нас событие, N — общее число возможных исходов какого-то процесса.

1) всего шаров 50+25+25=100

2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4

3) I= -(1/2*log₂1/2 + ¼*log₂1/4 + ¼*log₂1/4) = -(1/2*(0-1) +1/4*(0-2) +1/4*(0-2)) = 1,5 бит

Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно рассчитать по формуле 

Задача 2 В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?

т.к. N = 16 шаров,  то  I = log₂ N = log₂ 16 = 4 бит.

Упражнение  (устно)

1)    Какое количество информации будет получено при отгадывании числа из интервала:

-         от 1 до 64                   - от 1 до 61            -   от 1 до 20.

2)    Какое количество информации будет получено после первого хода в игре «крестики-нолики» на поле:

-         3x3                                   - 4x4.

3)    Сколько могло произойти событий, если при реализации одного из них получилось 6 бит информации.

Задача 3 В розыгрыше лотереи участвуют 64 шара. Выпал первый шар. Сколько информации содержит зрительное сообщение об этом?

Задача 4 В игре «лото» используется 50 чисел. Какое количество информации несет выпавшее число?

Задача 5 Какое количество информации несет сообщение о том, что встреча назначена на 3 июля в 18.00 часов?

Задача 6 Вы угадываете знак зодиака вашего друга. Сколько вопросов вам нужно при этом задать? Какое количество информации вы получите?

Задача 7 В ящике лежат фигурки разной формы - треугольные и круглые. Треугольных фигурок в ящике 15. Сообщение о том, что из ящика достали фигуру круглой формы, несет 2 бита информации. Сколько всего фигурок было в ящике?

Задача 8 В ведерке у рыбака караси и щуки. Щук в ведерке 3. Зрительное сообщение о том, что из ведра достали карася, несет 1 бит информации. Сколько всего рыб поймал рыбак?

Задача 9 Частотный словарь русского языка - словарь вероятностей (частот) появления букв в произвольном тексте — приведен ниже. Определите, какое количество информации несет каждая буква этого словаря.

Используя результат решения предыдущей задачи, определите количество информации в слове «КОМПЬЮТЕР».

Самостоятельная работа

по темам: «Измерение информации»

вариант № 1

1.     Перевести 67893300 бит в Мбайт.

2.     Перевести 0,031 Гбайт в биты.

3.     Укажите формулы, которые используются при алфавитном подходе.

4.     Определить информационный объем фразы: Мой дядя самых честных правил!

5.     Какое количество информации будет получено при отгадывании числа из интервала: а) от 1 до 128, б) от 0 до 510.

6.     В ящике лежат фигурки разной формы - треугольные и круглые. Треугольных фигурок в ящике 15. Сообщение о том, что из ящика достали фигуру круглой формы, несет 2 бита информации. Сколько всего фигурок было в ящике?

7.     Дать определение «Скорость передачи информации»

8.     Скорость передачи данных через ADSL – соединение равна 64000 бит/с. Передача файла через данное соединение заняла 5 мин. Определите размер файла в килобайтах.

9.     Дайте определение понятию Кодирование.

10. Изобразите схематично представление двоичного кода

Самостоятельная работа

по темам: «Измерение информации»

вариант № 2

1.     Перевести 89574500 бит в Мбайт.

2.     Перевести 0,029 Гбайт в биты.

3.     Укажите формулы, которые используются при вероятностном подходе.

4.     Определить информационный объем фразы: Я хочу поступить в университет!

5.     Какое количество информации будет получено при отгадывании числа из интервала: а) от 1 до 264, б) от 0 до 310.

6.     В ведерке у рыбака караси и щуки. Щук в ведерке 3. Зрительное сообщение о том, что из ведра достали карася, несет 1 бит информации. Сколько всего рыб поймал рыбак?

7.     Дать определение «Пропускная способность канала»

8.     Скорость передачи данных через ADSL – соединение равна 512000 бит/с. Передача файла через данное соединение заняла 7 мин. Определите размер файла в килобайтах

9.     Дайте определение понятию Декодирование.

10.  Изобразите схематично представление двоичного кода

Список используемой литературы

1)    Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 10-11 класс, 2012.

2)    М.С. Цветкова, Л.С. Великович, «Информатика и ИКТ», Москва, 2013

3)    Михеева Е.В. Информационные технологии в профессиональной деятельности. 2015 г.