Понятие модели, виды моделей

Понятие модели, виды моделей

Модель – схематическое представление того или иного предмета, с помощью выбранных средств моделирования.

Модель отражает основную структуру предмета и его свойства, существует большое количество классификаций моделей.

Модель – абстрактный образ объекта или явления и отношений между отдельными частями объекта или явления.

Любая модель это некоторая абстракция, звено в цепочке познания от опыта к абстракции, к осмыслению. Когда осмыслили снова опыту, к практике.

Процесс создания модели называется моделированием.

Существует несколько распространенных видов классификаций моделей определяющихся следующими принципами:

1)    областью использования (учебные модели, опытные модели, научно-технические модели, игровые модели);

2)    с учетом моделью временного фактора (статические и динамические модели);

3)    отрасль знаний (экономика, история, биология и др.);

4)    способ представления модели (материальные и абстрактные модели).

Учебные модели используются в процессе обучения – это обучающие программы, различные тренажеры, наглядные пособия.

Опытные модели – уменьшенные или увеличенные копии объекта, используемые для подробного исследования объекта и прогнозирования его будущих характеристик. Например: модель самолета, которая подвергается воздействию в аэродинамической трубе.

Научно-технические модели созданы для исследования процессов. К таким моделям можно отнести стенд для проверки работы схем, транзисторов и т. д..

Игровые модели – деловые, спортивные, экономические, военные и т. п. игры.

С помощью этих моделей можно разрешать конфликтные ситуации, оказывать психологическую помощь.

Имитационная модель –не просто отражает реальность с той или иной степенью точности, а имитирует ее.

Статическая модель – это единовременный срез информации по данному объекту.

Динамическая модель представляет собой картину изменения объекта во времени.

Материальные модели всегда имеют реальное воплощение и могут отражать:

1)    внешние свойства исходных объектов;

2)    внутренние устройства исходных объектов;

3)    суть процессов и явлений происходящих с объектами оригинала. (Примеры: скелет, чучело, робот).

Абстрактная модель не имеет естественного воплощения, основу этой модели составляет информация, она делится на мысленную и вербальную.

Мысленная модель возникает в процессе любой созидательной деятельности человека.

Вербальную модель человек использует для передачи своих мыслей другим (слова, разговор).

Информационные модели делятся на образно-знаковые и знаковые модели.

Фотографии, географические карты, диаграммы – это образно-знаковые модели, они учитывают цвет и форму. Их можно разделить на:

1)    геометрические (чертеж, план, карта, рисунок) отображающие внешний вид оригинала;

2)    структурные модели отображающие строение объектов и связи их параметров (таблица, граф, схема, диаграмма);

3)    словесные модели зафиксированные средствами языка;

4)    алгоритмическая модель(нумерованный список, блок-схема).

Знаковые модели делятся на:

1)    математические модели представленные математическими формулами, отображающие связи различных параметров объекта, системы, процесса;

2)    специальные модели представленные на специальных языках (химические формулы, ноты и др.);

3)    алгоритмические модели представлены в виде программы записанной на специальном языке программирования.

Имитационное моделирование – это процесс конструирования на ЭВМ сложной реальной системы функционирующей во времени и подстановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии обеспечив функционирование данной системы.

 Модель детерминированная

Если каждому входному набору параметров соответствует вполне определенный и однозначно определенный набор выходных параметров. В противном случае модель не детерминированная (стохастическая, вероятностная).

Пример: Рассматривается физическая модель свободного падения тела.

Данная модель является детерминированной.

Если бы учли случайный параметр, например порыв ветра с силой p при падении тела, то S считалось бы по другой формуле: S = (g(p) · t²)/2 и модель называлась бы стохастической.

Модель теоретико-множественная

Если она представима с помощью некоторых множеств и отношений принадлежности им и между ними.

Пример: Пусть задано множество X = Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна. Заданы отношения: Николай – супруг Елены, Екатерина – супруга Петра, Татьяна – дочь Николая и Елены, Михаил – сын Петра и Екатерины. Семья Николая и Петра дружат друг с другом. Множество X и множество перечисленных отношений Y  могут служить теоретико-множественной моделью двух дружеских семей.

Изобразить с помощью графов:

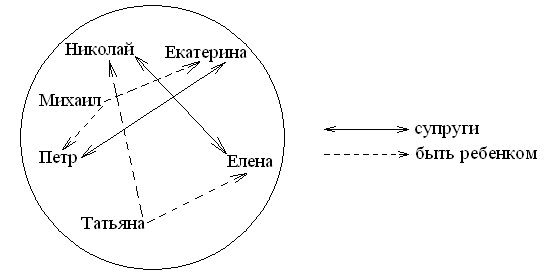
Модель логическая

Если она представима предикатами или логическими функциями.

Пример: Совокупность двух логических функций

может служить математической моделью  одноразрядного сумматора.

Модель игровая

Если она описывает, реализует некоторую  игровую ситуацию.

Модель алгоритмическая

Если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим её функции.

Пример: Алгоритмической моделью квадратного корня может служить алгоритм вычисления его приближенного сколь угодно точного отношения по известной рекуррентной формуле.

Модель языковая (лингвистическая)

Если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой.

Пример: Правило дорожного движения.

Языковая структурная модель движения транспорта и пешеходов.

Модель визуальная

Если она позволяет визуализировать отношения и связи моделируемой системы.

Модель натурная

Если она материальная копия объекта моделирования.

Пример: Глобус.

Модель геометрическая

Если она представима геометрическими образами и объектами.

Пример: Прямая линия является моделью числовой оси.

Параллелограмм является моделью плоскости, либо моделью квадрата.

 Модель клеточно-автоматная

Если она представляет систему с помощью клеточного автомата.

Пример:    Классическая   клеточно-автоматная модель: игра «жизнь» Дж. Конвея.

Модель фронтальная

Самая сложная, она описывает эволюцию моделируемой систему эволюции фронтальных объектов.

Пример: Множество Кантора.

Возьмем отрезок [0; 1] и разобьем его на три части.

Выбросим из донного отрезка средний отрезок и каждый из оставшихся отрезков опять разобьем на три части.

Из каждого отрезка выбросим средние части и каждый из оставшихся отрезков опять разобьем на три части.

Продолжая разбиение таким образом получим множество называемое множеством Квантора.

В пределе получаем несчетное множество изолируемых точек.

Фронтальная модель применяется обычно тогда, когда реальный объект нельзя представить в виде классической модели. Когда имеем дело с нелинейностью (много вариантностью) путей развития, необходимостью выбора и недетерминированностью (хаотичностью и необратимостью) процесса.

Пример: Математические модели динамики эпидемии инфекционной болезни, радиоактивного распада, усвоение второго иностранного языка и др..