Понятие степени. Степень с действительным показателем. Степень с рациональным показателем, свойства.

Лекция № 5

Тема: Понятие степени. Степень с действительным показателем. Степень с рациональным показателем, свойства.

Количество часов: 2 часа

Цель: обобщить и систематизировать знания о выполнении действий со степенями; добиться усвоения обучающимися понятий степени с действительным и рациональным показателями.

План:

1.       Понятие степени.

2.       Правила действий со степенями.

3.       Степень с рациональным показателем, свойства.

Вопрос 1. Понятие степени.

Степенью числа «а» с натуральным показателем «n», большим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «а»

Особые случаи возникают, если показатель степени равен единице или нулю (n =1; n = 0):

1.     Степенью числа «а» с показателем n=1 само это число:

2.     Любое число в нулевой степени равно единице:

3.     Ноль в любой натуральной степени равен нулю:

4.     Единица в любой степени равна 1:

Выражение 0⁰ считают лишенным смысла.

Например, ;     ;        

При решении примеров нужно помнить, что возведение в степень называется нахождением значения степени.

Примеры возведения в степень отрицательных чисел:

Вопрос 2. Правила действий со степенями

1.     Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):

Пример 1. 

Пример 2. 

Практически более важно обратное преобразование:

Пример 3.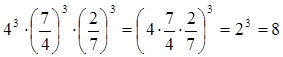 

Пример 4. 

2.     Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:

Пример 5.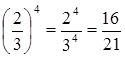 

Пример 6.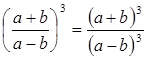 

Обратное преобразование: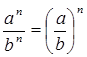

Пример 7. 

Пример 8. 

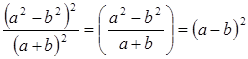
3.     При умножении степеней с одинаковыми основаниями показатели степеней складываются:

Пример 9. 

Пример 10. 

4.     При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого:

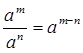
Пример 11. 

Пример 12. 

5.     При возведении степени в степень показатели степеней перемножаются:

Пример 13. 

Пример 14. 

Вопрос 3.Степень с рациональным показателем, свойства.

Выражениеозначает корень, показатель которого равен знаменателю nдроби , а показатель степени подкоренного числа равен числителю m дроби , т.е.

Например:

1.     Вычислить: 

Решение.

2.     Вычислить: 

Решение. Степень с дробным показателем для случая отрицательного основания не имеет смысла

Следует обратить внимание, что основание не может быть отрицательным числом, а показатель степени может быть как отрицательным, так и отрицательным.

Если - обыкновенная дробь, где  и а> 0, то под понимают :                   

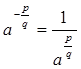
Вопросы для самопроверки:

1.     Что называется степенью числа?

2.     Какие правила действий со степенями вы знаете?

3.     Что означает степень с рациональным показателем?

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1.       Башмаков М.И., Математика: учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. – 7-е изд., стер. - М: Издательский центр «Академия», 2020. - 256с.

2.       Григорьев С.Г. Математика: учебник для студ. учреждений сред. проф. организация/ С.Г.Григорьев, С.В.Иволгина; под ред. В.А.Гусева. – 14-е изд., стер. – М.: Издательский центр «Академия», 2019. – 416 с.

3.       Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни – 5-е изд. -  М.: Просвещение, 2018. – 431 с.: ил.