Потенциал. Разность потенциалов. Эквипотенциальные поверхности. Связь между напряжённостью и разностью потенциалов электрического поля

Потенциал. Разность потенциалов. Эквипотенциальные поверхности. Связь между напряжённостью и разностью потенциалов электрического поля.

Понятие потенциала

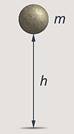
Если мы поднимем тело массы , лежащее на земле на высоту  (см. рис. 1), мы изменим его потенциальную энергию на величину . Именно такую работу  и необходимо совершить для этого подъема.

Рис. 1. Изменение потенциальной энергии

Для любой массы  разница энергий на высоте 0 и  будет равна  (см. рис. 2).

Рис. 2. Разница потенциальных энергий

Если разделить значение потенциальной энергии  на массу, мы получим величину, характеризующую гравитационное поле в данной точке. Выражение  уже не зависит от массы, оно показывает работу, которую необходимо совершить для переноса тела, с некоторой массой, на высоту , деленную на эту массу.

Теперь посмотрим, как ввести аналог потенциальной энергии приведенной на единицу массы в электрическом поле.

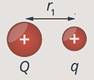
На заряд , находящийся в поле другого заряда , закрепленного в некоторой точке пространства, действует сила Кулона . Эта сила может переместить заряд , совершив при этом работу. Значит, система двух зарядов, находящихся на определенном расстоянии, обладает потенциальной энергией, зависящей от величины зарядов и расстояния между ними.

Если по аналогии с гравитационным полем рассмотреть величину, равную этой энергии, деленной на заряд , то она уже не будет зависеть от заряда  и охарактеризует только поле заряда  в данной точке. То есть будет являться функцией заряда  и расстояния между зарядами. Эта величина и называется потенциалом электрического поля.

Разность потенциалов двух точек, умноженная на величину заряда , равна работе, необходимой для перемещения этого заряда между этими точками. То есть разность потенциалов двух точек поля – это работа по перемещению между ними единичного заряда.

Как и в поле сил тяжести, эта работа не зависит от траектории  и определяется только положением точек, между которыми перемещается единичный заряд. Такие поля называют консервативными. В разделе «Механика» мы уже говорили, что энергия – величина, требующая для измерения задания «начала отсчета». Например, в гравитационном поле мы можем считать нулевой потенциальную энергию тела, находящегося на уровне земли. В случае электростатического поля, создаваемого зарядом, естественно считать нулевой потенциальной энергией некоторого заряда, находящегося в поле, его энергию на бесконечном удалении от заряда, в поле которого он находится. Это и есть «точка отсчета» для потенциальной энергии поля заряда.

Потенциал поля в некоторой точке равен работе по перемещению единичного заряда из этой точки на бесконечность.

Выражение для потенциала поля точечного заряда

  Пусть положительный заряд  находится на расстоянии  от положительного заряда  (см. рис. 3).

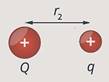Рис. 3. Изначальное положение заряда 

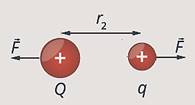Какую работу совершит электрическое поле при перемещении заряда  вдоль радиуса в точку, отдаленную на  от ? (см. рис. 4)

Рис. 4. Конечное положение заряда 

По определению работа силы равна этой силе, умноженной на перемещение:  В данном случае действует сила электрического взаимодействия (см. рис. 5), по закону Кулона .

Рис. 5. Действие силы электрического взаимодействия

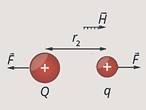Сила и перемещение в нашем случае сонаправлены,  и . Так мы можем находить работу для случая, когда сила постоянна на всей траектории. Здесь же сила изменяется по мере отдаления зарядов друг от друга.

Обозначим перемещение заряда (см. рис. 6).

Рис. 6. Перемещение заряда

По мере перемещения заряда  сила изменяется, но на малом (в сравнении с расстоянием до заряда ) отрезке можем считать ее постоянной и находить работу по определению, которое мы привели выше.

Работа, совершаемая силой Кулона на таком малом отрезке  равна , где силу  можно считать постоянной на всем отрезке . Тогда работа при перемещении на расстояние  будет равна сумме работ на  участках (), на каждом из которых сила Кулона постоянна и равна .

Эта сумма будет равна 

Эквипотенциальная поверхность

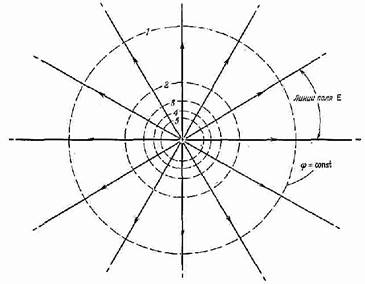Если рассмотреть поле, создаваемое точечным зарядом, то его напряженность падает по мере удаления от заряда в любом направлении. Следовательно, по мере удаления происходит и уменьшение потенциала поля. При этом в пространстве вокруг заряда можно указать ряд точек, обладающих одинаковым потенциалом.

Напомним, что точки, равноудаленные от некоторой заданной, образуют сферу. А значит, точки вокруг точечного заряда, обладающие одним и тем же потенциалом, также будут образовывать сферу с центром, лежащим в точечном заряде. Важное свойство этой сферы – при перемещении заряда по ней работа поля равна нулю, поскольку потенциальная энергия во всех точках этой поверхности одинакова. Нулевая работа перемещения также следует из того факта, что вектор напряженности перпендикулярен этой сфере (а значит, и направлению перемещения).

Рис. 1. Эквипотенциальные поверхности точечного заряда.

Поверхность, образованная точками с одним потенциалом, называется эквипотенциальной. Силовые линии и эквипотенциальные поверхности всегда взаимно перпендикулярны, а значит, работа поля по перемещению заряда по эквипотенциальной поверхности равна нулю. Плотность расположения эквипотенциальных поверхностей характеризует скорость изменения потенциала в данной области. Чем гуще расположены эквипотенциальные поверхности, тем быстрее меняется потенциал при движении перпендикулярно им.

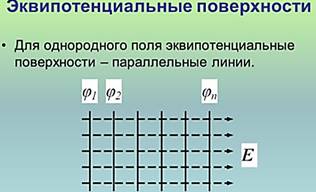
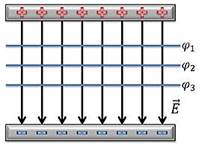
Для однородного поля, например, созданного двумя заряженными пластинами, эквипотенциальные поверхности представляют собой плоскости, параллельные пластинам. И в этом случае также перемещение заряда по любой поверхности равного потенциала происходит перпендикулярно вектору напряженности, а значит работа поля по перемещению равна нулю.

Рис. 2. Эквипотенциальные поверхности однородного поля.

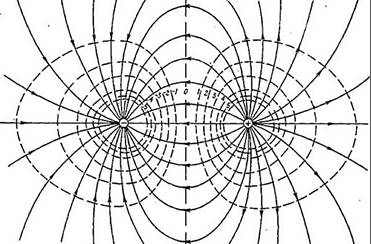
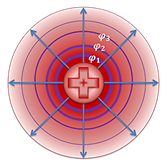
Для поля, образованного несколькими зарядами, эквипотенциальные поверхности имеют более сложную конфигурацию, однако, и в этом случае линии напряженности перпендикулярны этим поверхностям. Например, эквипотенциальные поверхности диполя выглядят следующим образом:

Отметим еще одно интересное свойство эквипотенциальных поверхностей – они могут располагаться плотнее и реже, но никогда не пересекаются.

Существуют две характеристики электрического поля: напряженность и разность потенциалов. Напряженность — это векторная величина, которая является силовой характеристикой поля:

Потенциал — это скалярная величина, которая является энергетической характеристикой поля:

Мы получили две формулы, описывающие работу поля при перемещении заряда: в одном случае работа выражена через напряженность, а во втором случае — через разность потенциалов, то есть, через электрическое напряжение:

Рис. 3. Эквипотенциальные поверхности диполя.

Исходя из этих двух формул, мы можем вывести связь между напряжением и напряженностью:

Итак, в данной формуле, Е — это напряженность поля, U — это разность потенциалов между некоторыми точками 1 и 2, а d — это вектор перемещения, соединяющий эти точки. Из формулы видно, что чем меньше меняется потенциал на расстоянии дэ, тем меньше напряженность поля. Если мы рассмотрим перемещение положительного заряда из точки 1 в точку 2, то убедимся, что поле совершает положительную работу. Это говорит о том, что потенциал в точке 1 больше, чем потенциал в точке 2. Поэтому, вектор напряженности электрического поля направлен в сторону убывания потенциала.

Необходимо отметить, что формула, связывающая разность потенциалов и напряженность справедлива только в том случае, если мы рассматриваем однородное поле. Заметим, тем не менее, что мы можем считать однородным любое электростатическое поле, при рассмотрении достаточно малой области пространства. Таким образом, наша формула также будет справедлива в том случае, если расстояние d настолько мало, что изменением напряженности на этом расстоянии можно пренебречь.

Рассмотрим еще один интересный случай: перемещение заряда в направлении, перпендикулярном линиям напряженности однородного поля.

Как вы понимаете, при этом перемещении, электрическое поле не совершает работу, поскольку вектор силы и вектор перемещения перпендикулярны. Из этого можно заключить, что все точки поверхности, перпендикулярной линиям напряженности обладают одинаковым потенциалом. Такие поверхности называют эквипотенциальными. Как видно из чертежа, эквипотенциальные поверхности однородного поля являются параллельными плоскостями. Что касается поля точечного заряда, то его эквипотенциальные поверхности представляют собой концентрические сферы.

Действительно, в каждой точке поверхности этих сфер, вектор напряженности перпендикулярен этим поверхностям. Следовательно, поверхность любой сферы, центром которой является точечный заряд, является эквипотенциальной.

Напомним, что когда мы рассматривали проводники в электростатическом поле, мы убедились, что все линии напряженности поля перпендикулярны поверхности проводника. Это означает, что поверхность любого проводника в электростатическом поле является эквипотенциальной. Также мы выяснили, что внутри проводника напряженность поля равна нулю. Следовательно, все точки внутри проводника обладают одинаковым потенциалом.