Повторение. Линейные уравнения и линейные неравенства.

Повторение. Линейные уравнения и неравенства.

Справочный материал.

Линейные уравнения.

Уравнение вида  k·x= b , где k – коэффициент (число), b – свободный член (число), х – переменная величина (неизвестная), называется линейным. Например, 5 ·х =20.

В зависимости от того, какие значения принимают «k» и «b», при решении линейных уравнений может быть три разных случая.

1)   k=0 ; b=0

0 ·х = 0 - здесь х может быть любым числом. Линейное уравнение имеет бесчисленное множество решений.

2)   k=0 ; b≠0

0 ·х = b – линейное уравнение не имеет решения.

Например,  0 ·х = 5  - нет решения.

3)   k≠0 ; b – любое число.

Линейное уравнение имеет единственное решение     x =  ;   5 ·х =20;  x =

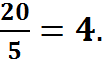
Разберем примеры.

1) Решить уравнение 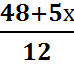  - 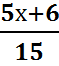 =7

Приведем обе части уравнения к общему знаменателю. Для этого разложим числа, стоящие в знаменатели, на простые множители.

12 = 3·2·2;  15 =3·5  Общим знаменателем будет число  3·2·2·5 =60. Найдем для каждой дроби недостающие множители и домножим на них

каждое выражение в левой и правой части уравнения.

 -  =.

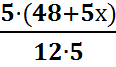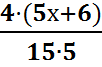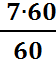Теперь знаменатели можно отбросить, а в числителе раскрыть скобки.

240 + 25х – 20х – 24 = 420

Соберем слагаемые, содержащие х в одной части уравнения, а не содержащие х перенесем в другую часть уравнения, поменяв их знак на противоположный.

25х – 20х= 420 – 240 + 24

5 ·х =204    x =   = 40,8    Ответ: 40,8

2)             Решить уравнение  2(1-2х) –х = 4(2-х) –х

2 - 4х - х= 8 - 4х – х ;  -4х – х +4х +х = 8 -2

-5х +5х =6 ;   0·х = 6  - нет решения.

Ответ : нет решения.

Линейные неравенства.

k·x > b;   k·x < b;    k·x b;    k·x b

k·x b;    k·x b   - нестрогие неравенства

k·x > b;   k·x < b  - строгие неравенства.

Линейные неравенства решаются также как уравнения, но при решении неравенств надо применять еще свойства линейных неравенств. 

Если обе части линейного неравенства умножить или разделить на число положительное, то знак самого неравенства не изменится.

 Если обе части линейного неравенства умножить или разделить на число отрицательное, то знак самого неравенства  изменится на противоположный (  на

>  на  <  и наоборот).

Примеры. 1) 4х -7 + 2 < 3 (4х +3) – 12х

4х -7 + 2 < 12х +9 -12х;   4х < 9 +5;  4х  < 14;   х<

 Ответ:    х<3,5   или  х

2) - 3х  18;  х ;   х

Ответ: х   или  х

Самостоятельная работа.

Вариант 1.

Решите линейные уравнения.

1.         -  х = 4

2.                      15 х +28 -3 х = -7 х -29

3.         = -  

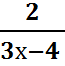4.                      6 ( 12 – х) = - 6 (х+1)

5. 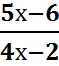        =2.5

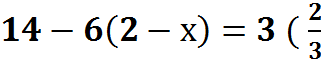6.          + 2х)

Решите линейные неравенства.

  7.   4х -2 (х-4) > - 4

  8.   5х +9 (1 – 2х)

  9.    – х -   3

Вариант 2.

Решите линейные уравнения.

1.      -  х = - 5

2.                  25 х +2х = 420 +21х

3.       =   

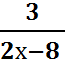4.      7 – 3 (2 –х) = 3 (  -х)

5.       =

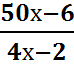6.                  36 -3з = 3 (х +11)

Решите линейные неравенства.

7.      – 4( 1 - 3х)  2 – 3х

8.       5х -3 (5х – 8)

9.            

Вариант  3.

Решите линейные уравнения.

1.      х = - 7

2.           13 -6х =2 (х+4)

3.     =   

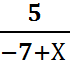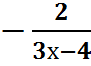
4.           10 – 2(Х – 4)= 1 - 2Х

5. 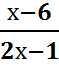    =  1

6.           5 – 2 ( 5Х -1) = 7 – 10 Х

Решите линейные неравенства.

7.    2( 4 +3х)  5 – 3х

8.    -   

9.   – 9 ( 7 + 3Х)

Вариант  4.

Решите линейные уравнения.

1.    -   х = - 6

2.           6 (2Х + 1) = 7Х – 3 - 2

3.     -  =   

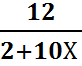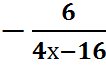
4.           2 ( 6 – х) = - 2 (х+6)

5. 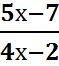    =0.5

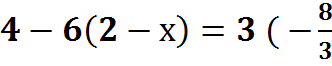6.      + 2х)

Решите линейные неравенства.

  7.   8х - 4 (х-4) > - 8

  8.   10х +9 (2 – 4х)

  9.    – 2х -   6