ПР 9. ВИЗНАЧЕННЯ ДОХОДНОСТІ І РИЗИКУ ПОРТФЕЛЮ

 ПР 9. Визначення доходності і ризику портфелю

9.1 Мета роботи

Метою заняття є отримання практичних навичків  з визначення доходності та ризику портфелю фінансових інструментів

9.2 Методичні вказівки з організації самостійної роботи студентів

При спробі розв'язати пряму або обернену задачу виникає запитання: яким чином визначаються характеристики портфеля (доходність та ризик). На сьогоднішній день найбільш розповсюджені 2 моделі визначення характеристик портфеля: модель Марковіца та модель Шарпа.

Модель Марковіца

Модель базується на тому, що показники прибутковості різних цінних паперів взаємопов'язані: із зростанням доходності одних паперів спостерігається одночасне зростання і по іншим паперам, треті залишаються без змін, а в четвертих, навпаки доходність знижується. Такий вид залежності не детермінований, тобто однозначно визначений, а є стохастичним, і називається кореляцією.

Модель Марковіца має наступні основні припущення:

·                    за доходність цінних паперів приймається математичне очікування доходності;

·                    за ризик цінних паперів приймається середнє квадратичне відхилення доходності;

·                    вважається, що дані минулих періодів, які використані при розрахунках доходності і ризику, повністю відображають майбутні значення доходності;

·                    ступінь і характер взаемозв'язку між цінними паперами виражається коефіцієнтом лінійної кореляції.

За моделлю Марковіца доходність портфеля цінних паперів — це середньозважена доходність паперів, його складових, яка визначається формулою:

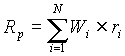
де:
N — кількість цінних паперів, які розглядаються;
W_i — процентна частка даного паперу в портфелі;
r_i — доходність даного паперу.

Ризик портфеля цінних паперів визначається функцією:

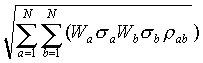
де:
W_i — процентна частка даних паперів у портфелі;
s_a s_b — ризик даних паперів (середньоквадратичне відхилення)
r_ab — коефіцієнт лінійної кореляції

З використанням моделі Марковіца для розрахунку характеристик портфеля пряма задача набуває вигляд:

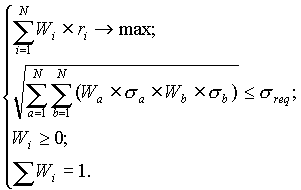
Обернена задача розраховується аналогічно:

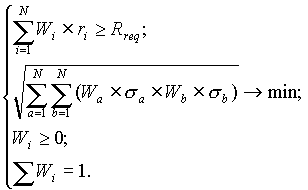
При застосуванні моделі Марковіца на практиці для оптимізації фондового портфеля використовуються наступні формули:

1) доходність цінних паперів:

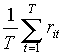
де:
T — кількість мину лих спостережень доходності даних цінних паперів;

2) ризик цінного паперу:

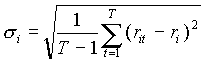
3) коефіцієнт кореляції між двома цінними паперами:

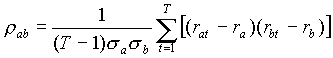
де:
r_at, r_bt — доходність цінних паперів а та b в період t

1                   Модель ефективного портфеля з безризиковим компонентом (задача Тобіна)

Ця задача відрізняється від моделі (3.1)-(3.4) тим, що інвестор крім ризикових цінних паперів враховує також можливість безризикових вкладень з ефективністю  в частках . Задача Тобина формулюється  так – знайти частки ,  що мінімізують  ризик портфеля

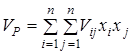 ,                                     (3.5)

при обмеженнях

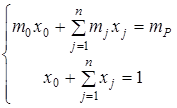                     (3.6)

З задачі Тобина випливає поняття  цінного папера. Величина  -го цінного папера показує, яка частина ринкової прибутковості припадає на прибутковість -ї фірми

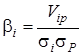 ,                                               (3.7)

де  – коваріація доходностей ї фірми і ринкового портфеля;

 –  ризик го цінного папера і ринкового портфеля.

Тоді прибутковість -го цінного папера, що входить у портфель, визначається за формулою

.                              (3.8)

Якщо , то це означає, що прибутковість дохідного -го цінного папера більше ринкової прибутковості; при  – її прибутковість дорівнює ринкової; при  – прибутковість цінного папера менше ринкової, але більше, ніж безризиковий відсоток  .

Ринкова ціна ризику  визначається у вигляді:

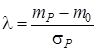 ,                                             (3.9)

де  – прибутковості портфеля цінних паперів і безризикова прибутковість;

 – ризик портфеля.

Приклад 7.6.Сподівана норма прибутку акцій виду А1 становить 60%, ризик цих акцій (середньоквадратчне відхилення) — 20%. Для акцій виду А2 відповідно сподівана норма прибутку — 40%, ризик — 15%. Коефіцієнт кореляції для цих акцій r12 = 0,35. На основі цих акцій створюється ПЦП. Необхідно:

• обчислити сподівану норму прибутку та ризик ПЦП, якщо акції виду А1 складають 20% вартості цього портфеля;
• обчислити сподівану норму прибутку та ризик ПЦП, якщо акції виду А1 складають 80% вартості ПЦП;

!  створити оптимальний ПЦП (тобто такий, що має мінімальний ризик).
Розв’язання. 1) Згідно з умовою частка акцій виду А1 в ПЦП х1 = 0,20, а тому частка акцій виду А2 х2 = 0,80. Тоді

2) Оскільки в цьому випадку  х1= 0,80,  х2 = 0,20, то отримуємо:

3) Оскільки  то


-
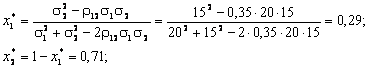
Приклад 7.7.Виходячи з умови прикладу 7.6, знайти структуру ПЦП:
а) сподівана норма прибутку якого становила б 50%; б) ризик якого становив би 16%.

! Розв’язання. а) Скориставшись тим, що
,
  отримуємо систему рівнянь:
.
  Розв’язавши цю систему рівнянь, отримуємо, що x1 = 0,5, x2 = 0,5,
.
  б) Скориставшись тим, що
,
  отримуємо систему рівнянь
.
  Ця система рівнянь зводиться до квадратного рівняння:
  415 x12 – 240 x1 – 31 = 0,
  яке має корені x? = – 0,109 та x?? = 0,687. Оскільки x? < 0, то в ПЦП частка ЦП виду A1 становить x1 = x?? = 0,687, виду A2 — x2 = 1 –
  – x?? = 0,313.
  Сподівана норма прибутку отриманого ПЦП становить
mП = x1m1 + x2m2 = 0,69 ? 60 = 0,31 ? 40 = 53,84(%).-

Приклади аудиторних задач

1. Инвестор намерен за счет сбережений сформировать портфель из двух разновидностей ценных бумаг. Первая из них имеет:  вторая соответственно  Отношение инвестора к риску представлено функцией полезности    где   и - соответственно доходность и степень риска портфеля. Определить оптимальную структуру портфеля для  инвестора.

2. Сформируйте портфель минимального риска из двух разновидностей ценных бумаг:

 ,   .

Рассчитайте для трех коэффициентов корреляции, равных -0,5;  0,5;  0,9

3. Определить доходность и риск () портфелей, сформированных из двух ценных бумаг А и Б. Просчитать показатели для таких  соотношений А и Б в портфеле как : а) 100% А; б) 70% А и 30 % Б; в) 30% А и 70 % Б; г) 100% Б.

Использовать значения коэффициента корреляции между ценными бумагами А и Б на уровне: а) -0,5; б) 0,5; в) 0,9

Скачано с www.znanio.ru