Практическая (контрольная) работа "Код с проверкой на четность " МДК.01.01. Компьютерные сети
Фамилия ________________________________________ Группа__________
1. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
2. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
1 |
1 |
|
|
1 |
0 |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
0 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
3. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
Если нечетное количество единиц, добавляем 0.
Если четное количество единиц, добавляем 1.
Ноль –четное число
Фамилия ________________________________________ Группа__________
1. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
0 |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
2. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
0 |
|
|
1 |
1 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
1. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
1 |
1 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
Если нечетное количество единиц, добавляем 0.
Если четное количество единиц, добавляем 1.
Ноль –четное число
Теоретический блок
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Код с проверкой на четность
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
В каждом пакет данных есть один бит четности, или, так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно . Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
Ниже показана структурная схемы кодера для данного кода
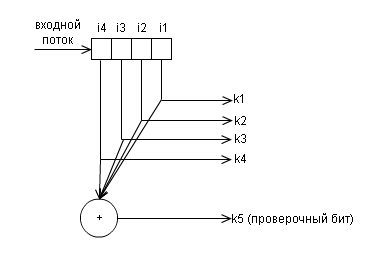
и и декодера
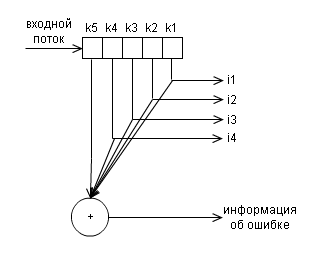
Пример:
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.
Как говорилось ранее, этот метод служит только для определения одиночной ошибки. В случае изменения состояния двух битов, возможна ситуация, когда вычисление контрольного бита совпадет с записанным. В этом случае система не определит ошибку, а это не есть хорошо. К примеру:
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.
Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в
процессе передачи информации допустим ошибку (ошибка нолик вместо единицы,
желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце,
третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в
0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Ответы.
Вариант 1.
1. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
2. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
3. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Если нечетное количество единиц, добавляем 0.
Если четное количество единиц, добавляем 1.
Ноль –четное число
Вариант 2.
3. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
4. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
2. Построить прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку.
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
Если нечетное количество единиц, добавляем 0.
Если четное количество единиц, добавляем 1.
Ноль –четное число
Фамилия ________________________________________
Фамилия ________________________________________
Теоретический блок Параметры помехоустойчивого кодирования
Пример: Начальные данные: 1111
В этом случае система не определит ошибку, а это не есть хорошо
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку
Ответы. Вариант 1. 1.
Если четное количество единиц, добавляем 1
Если нечетное количество единиц, добавляем 0
© ООО «Знанио»
С вами с 2009 года.
