Практическая работа № 5 Тема: Расчет разветвленной R-L-C цепи переменного тока, резонанс токов.

Практическая работа № 5

Тема:  Расчет  разветвленной R-L-C цепи переменного тока, резонанс токов.

Цель работы: исследование электрической цепи синусоидального тока при последовательном соединении резистора, индуктивной катушки и конденсатора. Научиться  по опытным  данным строить векторные диаграммы токов и напряжений, определять параметры электрической цепи. Понимать и уметь устанавливать резонанс напряжений в рассматриваемой цепи.

Краткая теория

     Под резонансом  в электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, а эквивалентная схема представляет собой активное сопротивление.

Резонанс в электрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот.

     При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках.

     В цепи, где  элементы    соединены последовательно (последовательный колебательный контур) может возникнуть резонанс напряжений, а в цепи, где элементы     соединены параллельно, – резонанс токов.

     Основными характеристиками   колебательного контура являются резонансная частота циклическая   или линейная  добротность контура и характеристическое сопротивление .  В последовательном колебательном контуре добротность показывает, во сколько раз происходит увеличение амплитуды колебаний напряжения в индуктивности и емкости  при резонансе по отношению к входному напряжению

      Характеристическое сопротивление контура  равно реактивному сопротивлению   индуктивности и емкости  при резонансе

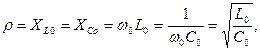
      Для цепи с последовательным соединением катушки индуктивности и конденсатора справедливо соотношение

,                 (1)

                      где     и   - комплексное и полное сопротивление контура,   – угол сдвига фаз между напряжением и током.

                                                                              (2)

При резонансе    и     поэтому  из (1) следует, что это возможно, если

                                                               (3)

 Это выражение называют условием резонанса напряжений.

В зависимости от соотношения величин  и  возможны три различных случая:

 1 ,  следовательно  .  Этому режиму соответствует векторная диаграмма,  изображенная на рисунке 1а.

2  , следовательно  -  резонанс напряжений (рисунок 1б).

3  ,  следовательно .  Этот  случай изображен  на рисунке 1с.

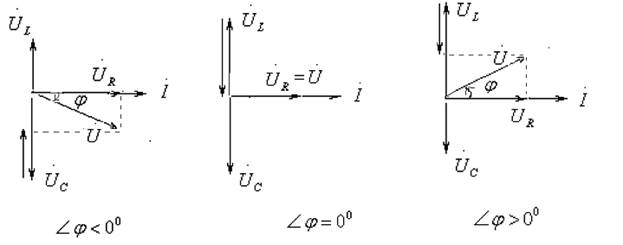
        а)                                  б)                                            с)

Рисунок 1

В области до резонанса при w<w₀ цепь носит ёмкостный характер, в резонансе ( w=w₀ )  - активный, а после резонанса  при w>w₀ – индуктивный характер.

Выразив  и   из   (3),  соответственно, через     и  получим

,    откуда  ,  

 где   - резонансная частота.    

     При  резонансе напряжений  ток  в цепи  резко  возрастает:

.

 Соответственно увеличиваются  и напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания  (при условии ).  Коэффициент усиления напряжения на  реактивных  элементах   (добротность контура - Q):

На рисунке 2 показаны графики  характеристик последовательного резонансного контура   .

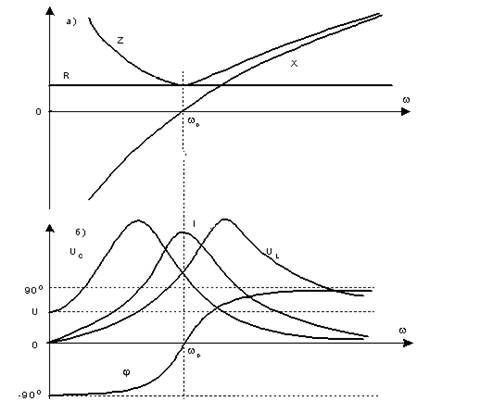
Рисунок 2

В области до резонанса при w<w₀ цепь носит ёмкостный характер, в резонансе ( w=w₀ )  - активный, а после резонанса  при w>w₀ – индуктивный характер.

Интервал частот на границах которого ток  называют полосой пропускания  - . Относительная полоса пропускания называется затуханием цепи:  .

 Затухание цепи связано с добротностью контура соотношением   

Порядок выполнения работы

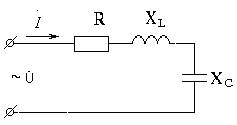
• Собрать схему исследования  (рисунок 3).

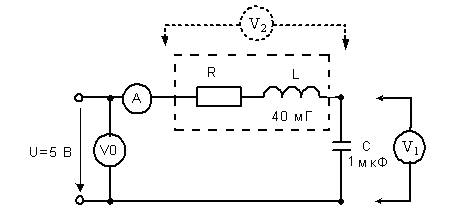
Рисунок 3

• Измерить  омметром  активное сопротивление  катушки  индуктивности.

• Рассчитать теоретическую резонансную частоту  , характеристическое сопротивление  ,    добротность   и затухание контура  -  по формулам:

,         ,          ,          .

• Установить параметры регулируемого источника синусоидального напряжения: =5В, =. Включить виртуальные приборы и, изменяя частоту приложенного напряжения, добиться резонанса по максимальному току. Для более точной настройки резонансного режима проверить показание фазометра.

• Измерить  параметры электрической цепи. Результаты расчетов и измерений занести в таблицу 1.

Таблица 1

• Изменяя частоту от  0,2 до  2, записать в таблицу 2 показания виртуальных   приборов    и    по   этим    результатам     построить    графики

частотных характеристик последовательного резонансного контура       

 Таблица 2

• По экспериментальным данным определить добротность контура   и  затухание цепи  .    Сравнить их  с теоретическими значениями.

 • Построить векторные диаграммы напряжений и тока для трех значений частоты:  ,    и  .

 • Сделать выводы по работе.

Контрольные вопросы и задачи

1  В чем заключается явление резонанса напряжений  и при каком условии оно возникает? Перечислите все особенности цепи при резонансе напряжений.

2  Каков характер цепи  до резонанса, в резонансе и после резонанса?

3  Изменяя  какие параметры цепи, можно получить резонанс напряжений?

4 С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений?

5  Что такое добротность контура и на что она оказывает влияние?

6  Почему при резонансе напряжений ток в цепи максимальный?

7 Определить резонансную частоту последовательного колебательного контура с параметрами:  1 Гн,  С=100 мкФ,   R =10 Ом.

8  Определить ток последовательного колебательного контура при резонансе напряжений, если его параметры   20 мГн,  С=2 мкФ, добротность  =50, напряжение контура   U=2 B.

9  Определить индуктивность  и емкость   последовательного колебательного контура, если его характеристическое сопротивление   = 300 Ом, резонансная частота f₀ = 2 МГц.

10 Определить частоту сети, при которой в цепи возможен резонанс напряжений. Определить  также,  во сколько раз напряжение  на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры:   0,1 Гн,   R= 20 Ом,   C= 5 мкФ.

Выполнение работы

Для получения зачета необходимо оформить отчет:

1. Изучить методическую разработку

2. Выполнить конспект

3 Проверить техническую документацию.

4 Сделать вывод о проделанной работе.

Преподаватель                              Казетов С.Н.

Скачано с www.znanio.ru