Практическая работа № 6. Наращенная сумма обыкновенной ренты

Практическая работа № 6. Наращенная сумма обыкновенной ренты с однократным и m-кратным начислением процентов.

Задача формирования инвестиционного фонда с использованием финансовых функций MS Excel

Задание 1. Решить две задачи для своего варианта. Решение оформить так же, как предыдущие работы (на рабочем листе должно быть: постановка задачи, исходные данные, результаты решения; применить формат к различным фрагментам рабочего листа, см. рис. 1 и рис. 2). Выполнить анализ результата, сделать выводы.

Варианты заданий для решения задачи 1 представлены в табл. 1, задачи 2 – в табл. 2. Номер варианта равен номеру логина. Если номер логина больше 15, то номер варианта равен номер логина минус 15.

Задача 1. В страховую компанию 1 раз в год поступают страховые взносы R. Страховая компания эти взносы помещает в банк под определенную процентную ставку годовых j (номинальная ставка сложных процентов). Начисление процентов осуществляется m раз в году при сроке ренты n лет. Найти наращенную сумму S обыкновенной ренты (постоянного аннуитета постнумерандо) с однократным и m – кратным начислением процентов.

Указания по решению задачи 1

Наращенная сумма S ренты с однократным начислением процентов j (годовых) в конце периода (года) за срок ренты n (лет) вычисляется по формуле

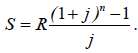
Наращенная сумма S ренты с m– кратным начислением процентов j (годовых) за срок ренты n (лет) вычисляется по формуле

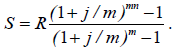
Таблица 1 – Варианты задания к задаче 1

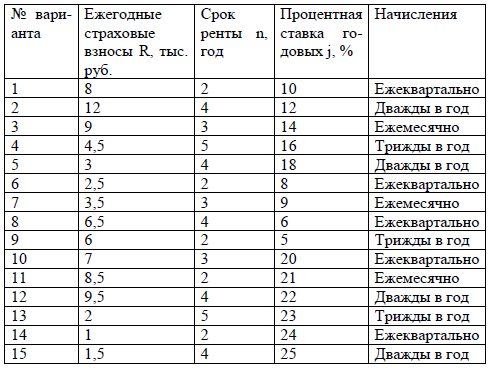
Задача 2. Компания решила создать инвестиционный фонд. Для этого в конце каждого года в течение n лет в банк вносится очередной платеж R (все платежи равны) под известную процентную ставку годовых i (одинакова для всех платежей). Производится капитализация платежа – он прибавляется к уже накопленной сумме.

1. Составить таблицу накопления сумм процентов для каждого из периодических платежей. Поэтапно (по каждому году) показать, как увеличивается сумма каждого отдельного платежа по мере по годичного роста суммы процентов от этого платежа.

2. Вычислить наращенный денежный поток аннуитета постнумерандо в течение срока ренты (n лет) (сумму потока) и за каждый период (k–й год).

3. Величину наращенного денежного потока ренты вычислить тремя способами: а) как сумму всех элементов денежного потока; б) используя финансовую формулу; в) используя функцию MS Excel БС().

4. Вычислить коэффициент наращения ренты.

Образец оформления результата решения задачи 2 на рабочем листе представлен на рис. 2.

Таблица 2 – Варианты задания к задаче 2

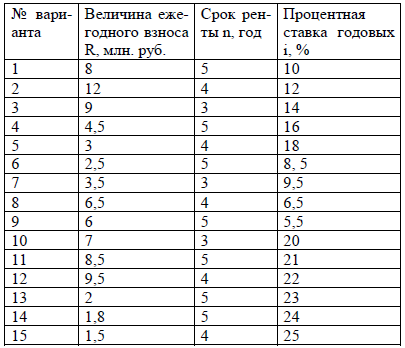
Указания по решению задачи 2

Коэффициент наращения ренты можно вычислить как отношение наращенной суммы к размеру однократного платежа – S/R или прямым расчетом по формуле коэффициента.

На рис. 1 представлено решение задачи для исходных данных: срок аннуитета постнумерандо n=5, ежегодный платеж R= 1 руб., процентная ставка годовых i=10%. Показано решение, которое представляет собой «аннуитетный треугольник» постнумерандо.

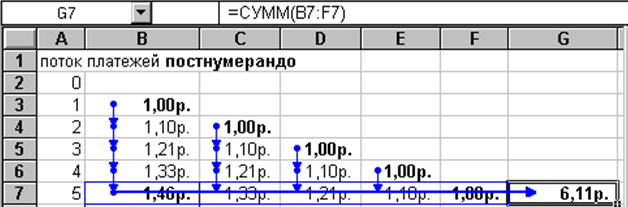
Рисунок 1 – «Аннуитетный треугольник» постнумерандо

Это треугольник размером nхn, на диагонали которого указана величина взноса; заголовки строк – периоды очередного взноса (год k); столбцы – порядковые номера взноса. В столбце B – вычисленная сумма (k-й платеж + проценты к моменту n), наращенная на платеж, сделанный в момент k, к моменту n. По строкам указана последовательность наращения по сложным процентам в момент k (значения повторяются).

Наращенная величина вычисляется по формуле:  Указанную формулу можно использовать для вычисления элемента наращенного потока платежей, как это показано в примере на рис. 2, или использовать функцию MS Excel БС(норма; число_периодов; выплата; текущая стоимость;тип), как это показано ниже для рис. 2.

Для расчета величины B7 (1,46р.) используется формула:

=БС(0,1;4;0;-1;0), или =БС(0,1;4;0;-1;0), или =БС(0,1;4;;-1) – будущая стоимость одного вложенного рубля (текущая стоимость=-1) после четырех раз (число_периодов=4) присоединения к нему процентных денег, начисляемых в конце периода по ставке 10 сложных процентов (норма=0,1) без дополнительных поступлений и выплат. В связи с полным отсутствием в течение срока промежуточного потока платежей нет смысла уточнять и момент их поступления в нулевом размере (выплата=0), тип=0 (значение используется по умолчанию) для аннуитета постнумерандо (тип= 1 для аннуитета пренумерандо).

Для расчета величины G7 (6,11р.) – наращенной суммы аннуитета используется формула:

=БС(0,1;5;-1;0;0), или =БС(0,1;5;-1;0;0), или =БС(0,1;5;-1) – будущая стоимость потока пяти периодических платежей (число_периодов=5) единичного размера, вносимых (выплата=-1) регулярно в конце периода (потоку постнумерандо соответствует тип=0, значение используется по умолчанию) при начислении 10 сложных процентов (норма=0,1) за период между моментами внесения платежей на поступившие ранее средства.

Во всех формулах MS Excel для операндов должны быть указаны ссылки на ячейки с данными, а не абсолютные значения.

Рисунок 2 – Образец оформления результата решения задачи 2

Задание 2. Решить задачу 2 для постоянного аннуитета пренумерандо для тех же исходных данных. Пример решения приведен на рис. 3.

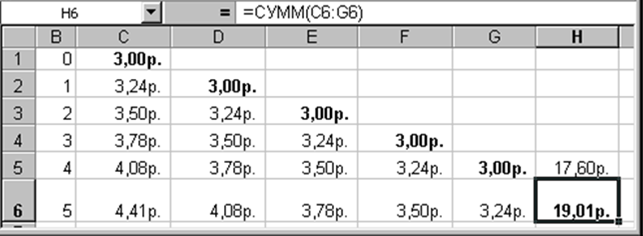
Рисунок 3 – «Аннуитетный треугольник» пренумерандо