Практическая работа метод Гаусса

Группа: Тв-21, Тв-22

УД: Математика

ФИО преподавателя: Никонова Н. С.

Дата проведения занятия (занятий): 22 апреля 2020

Дата выполнения задания: 22 апреля 2020

Вид занятия - Практическая работа – 2 часа

Тема занятия: «Решение систем линейных уравнений третьего порядка методом Гаусса»

Цели работы:

-     расширить представление о методах решения СЛУ и отработать алгоритм решения СЛУ методом Гаусса;

-      развивать логическое мышление студентов, умение находить рациональное решение задачи;

-     воспитывать у студентов культуру письменной математической речи при оформлении ими своего решения.

Задание:

1.      Ознакомиться с теоретическим материалом и оформить краткий конспект теории и разобранных примеров в тетради

2.      Выполнить самостоятельную работу

Форма отчета:

1.      Отчет оформить в текстовом документе (Word): в документ вставить фотоотчет из тетради по плану:

a.       Тема занятия

b.      Цель

2.      Отчет отправить не позднее 22 апреля по ссылке https://vk.com/topic-193207144_40540306 .

Основной теоретический материал.

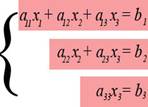Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной (см. рисунок).

Рассмотрим алгоритм решения методом Гаусса на конкретном примере.

Решить систему линейных уравнений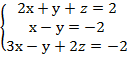 

Применим прямой ход – получим нули под главной диагональю. Для этого:

Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду.

Вначале поменяем первую и вторую строку,

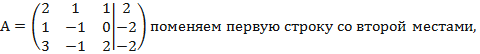
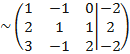
Выполним преобразования, благодаря которым получим нули под главной диагональю в первом столбце.

Для этого от второй строки отнимаем две первых, от третьей - три первых:

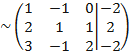
Т.е. каждый элемент первой строки мы умножаем на 2 и вычитаем из соответствующих элементов второй строки

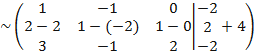
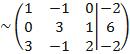
Каждый элемент первой строки умножаем на 3 и вычитаем из соответствующих элементов третьей строки

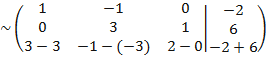
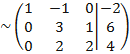         , таким образом получили новую матрицу.

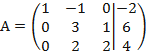
Все элементы третьей строки делим на два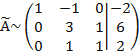      

Выполним преобразования, благодаря которым получим нули во втором столбце под главной диагональю.

Для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

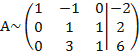
От третьей строки отнимаем вторую, умноженную на 3:

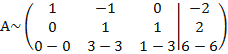 получаем новый вид  А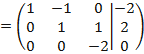 

Разделим третью строку на (-2), получаем: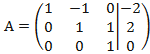

Проведем теперь обратный ход, то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца.

Надо обнулить элемент , для этого от второй строки отнимем третью:

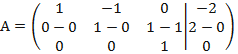  получаем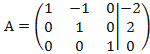   

Далее обнуляем недиагональные элементы второго столбца а₁₂, к первой строке прибавляем

вторую:     получаем 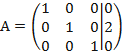  приведем к

неизвестным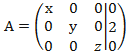 таким образом, полученной матрице соответствует система

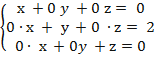             отсюда следует                         Ответ: (0,2,0)

Задания для самостоятельного решения:

ВАРИАНТ 1

Решите системы линейных уравнений методом Гаусса:

А)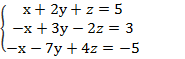   

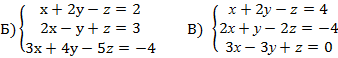
Критерии оценивания:

«3», если: записано решение примера и выполнена проверка решения системы;

самостоятельно методом Гаусса верно решена одна из систем.

 «4», если: самостоятельно методом Гаусса верно решены любые две системы.

«5», если: самостоятельно методом Гаусса верно решены три системы.

Скачано с www.znanio.ru