Практическая работа Метод Крамера

Группа: Тв-21, Тв-22

УД: Математика

ФИО преподавателя: Никонова Н. С.

Дата проведения занятия (занятий): 15 апреля 2020

Дата выполнения задания: 16 апреля 2020

Вид занятия - Практическая работа – 2 часа

Тема занятия: «Решение систем линейных уравнений третьего порядка методом Крамера»

Цели работы:

-          расширить представление о методах решения СЛАУ (система линейных алгебраических уравнений) и отработать алгоритм решения СЛАУ методом Крамера, закреплять точность вычислений;

-          развивать логическое мышление, умение находить рациональное решение задачи;

-          воспитывать внимательность, аккуратность и культуру письменной математической речи при оформлении ими своего решения.

Задание:

1.      Ознакомиться с теоретическим материалом и оформить краткий конспект теории и разобранных примеров в тетради

2.      Выполнить самостоятельную работу – 1 вариант – аудиторная работа, 2 – вариант – домашнее задание.

Форма отчета:

1.      Отчет оформить в текстовом документе (Word): в документ вставить фотоотчет из тетради по плану:

a.       Тема занятия

b.      Цель

2.      Отчет отправить не позднее 10 апреля по ссылке https://vk.com/topic-193207144_40458583.

Критерии оценивания:

Теоретический материал.

Задана система N линейных алгебраических уравнений с  неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами - числа

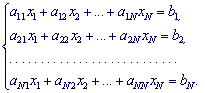Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй - при котором из неизвестным он находится.

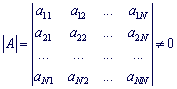Если определитель матрицы не равен нулю, то система линейных алгебраических уравнений имеет единственное решение.

Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность  чисел , которая при превращает каждое из уравнений системы в правильную равенство.

Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной.

В случае, когда некоторые из них отличны от нуля – неоднородной   

Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае - несовместимой.

Если решение системы единственное, то система линейных уравнений называется определенной.

В случае, когда решение совместной системы не единственное, систему уравнений называют неопределенной.

Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот.

Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.

Эквивалентные преобразования СЛАУ

1) перестановка местами уравнений;

2) умножение (или деление) уравнений на отличное от нуля число;

3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.

Теорема Крамера. 

Если определитель системы  линейных алгебраических уравнений с  неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:    - определители, образованные с  заменой -го столбца, столбцом из свободных членов.

Если , а хотя бы один из  отличен от нуля, то СЛАУ решений не имеет.

Если же , то СЛАУ имеет множество решений.

Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера

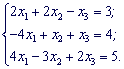Решение.

Найдем определитель матрицы коэффициентов при неизвестных

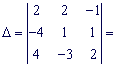
Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:

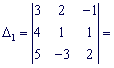
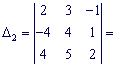
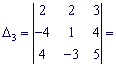
По формулам Крамера находим неизвестные

Итак единственное решение системы.

Задача 2* (на дополнительную оценку).

Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.

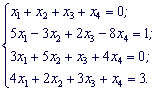
Решение.

Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.

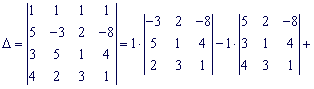
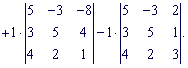
Найдем составляющие определителя:

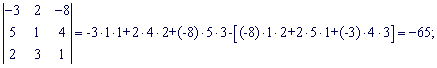
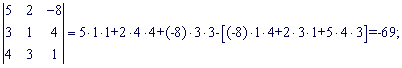
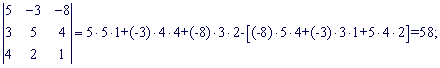
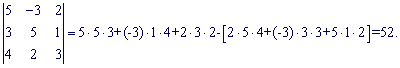
Подставим найденные значения в определитель

Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:

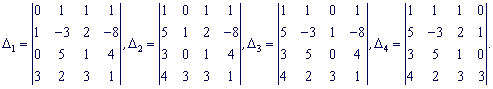
Разложим каждый из определителей по столбцу в котором есть больше нулей.

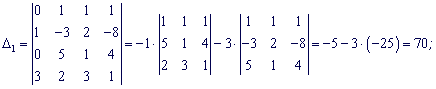
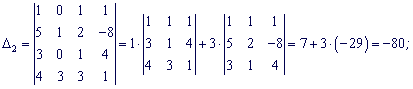
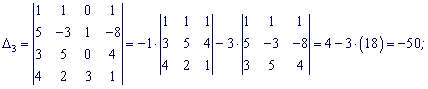
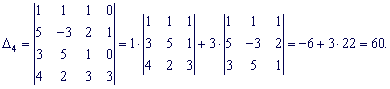
По формулам Крамера находим

Решение системы 

Задания для самостоятельного решения:

Критерии оценивания:

Работа оценивается на «3»,если:   самостоятельно полностью и верно решена одна из систем.

Работа оценивается на «4»,если:   самостоятельно полностью и верно решены любые две системы.

Работа оценивается на «5»,если:   самостоятельно полностью и верно решены три системы.