Практическая работа на тему:" Решение прикладных задач с помощью определенного интеграла"

Практическая работа №3

Тема: «Решение прикладных задач с помощью

определенного интеграла»

 

Цель: уметь применять определенный интеграл к решению задач прикладного характера, а именно нахождение площадей криволинейных трапеций и объемов тел вращения.

 

Оборудование: ручка, карандаш, линейка, методические рекомендации по выполнению работы.

 

Методические рекомендации по выполнению практической работы:

Задание №1. Найти площадь фигуры, ограниченной линиями:

а) ;

б) ;

в)

 

Решение:

а)

Рассмотрим уравнения данных кривых:

 - парабола, ветви направлены вверх.

Найдем вершину параболы

Итак, наша парабола имеет вершину .

Построим таблицу значений для нашей параболы:

 - уравнение прямой, построим для нее таблицу значений:

Построим теперь графики параболы  и прямой  в одной системе координат. Область между этими кривыми и будет искомой площадью нашей криволинейной трапеции.

Найдем координату x точек пересечения рассматриваемых графиков следующим образом:

 

Найдем теперь площадь криволинейной трапеции:

 

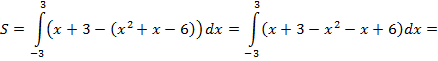
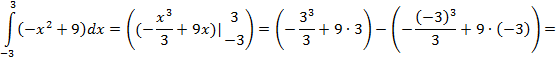
Ответ:

 

 

б)

 

Рассмотрим уравнения данных кривых:

1)  - парабола, ветви направлены вверх.

Построим таблицу значений для нашей параболы:

2)  - парабола, ветви направлены вниз.

Построим таблицу значений для нашей параболы:

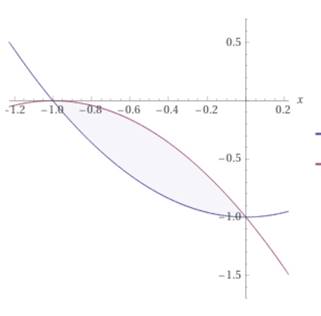
Построим теперь графики данных парабол  и  в одной системе координат. Область между этими кривыми и будет искомой площадью нашей криволинейной трапеции.

Найдем координату x точек пересечения рассматриваемых графиков следующим образом:

Найдем теперь площадь криволинейной трапеции:

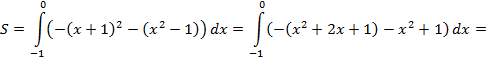
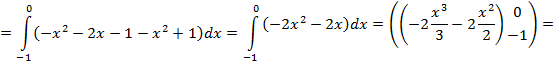
Ответ:

 

 

в)

 

Рассмотрим уравнения данных кривых:

1) , так как , то построим таблицу значений для нашей функции:

2)  - это уравнение оси OX.

 

Построим теперь криволинейную трапецию, ограниченную рассматриваемыми графиками.

 

 

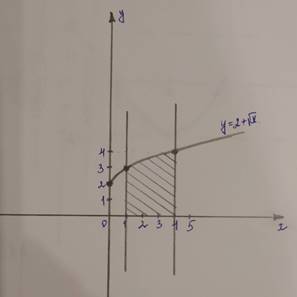
Найдем теперь площадь криволинейной трапеции:

 

 

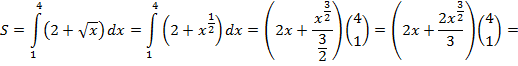
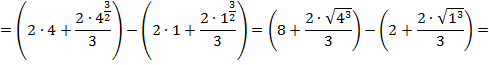
Ответ:

 

Задание №2.  Вычислить объем тела вращения, полученный при вращении кривой:

а)  вокруг оси OX;

б)  вокруг оси OY.

 

Решение:

а)  вокруг оси OX

 

Построим график уравнения  на отрезке .

 

 

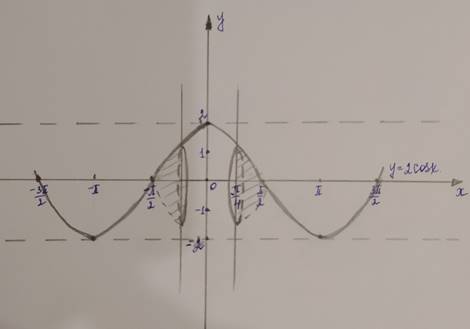
Так как необходимо вычислить объем тела вращения, полученный при вращении кривой  вокруг оси OX, то воспользуемся формулой:  , где .

Итак, искомый объем данного тела вращения равен:

 

=

=

 

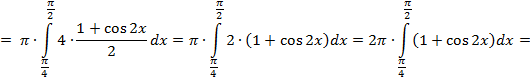
Ответ:

 

 

б)  вокруг оси OY.

 

Построим график уравнения  на отрезке , так как , то есть , откуда

, откуда

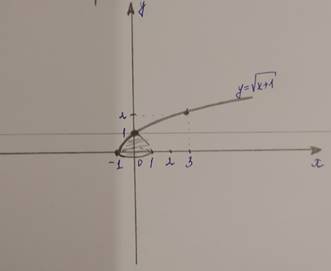
Так как необходимо вычислить объем тела вращения, полученный при вращении кривой  вокруг оси OY, то воспользуемся формулой:  , где .

 

Выразим x из уравнения , а именно

Тогда искомый объем данного тела вращения равен:

 

 

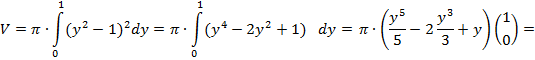
Ответ:

 

Задания для самостоятельной работы:

 

Вариант №1   Задание №1. Найти площадь фигуры, ограниченной линиями: а) ; б) ; в)   Задание №2.  Вычислить объем тела вращения, полученный при вращении кривой: а)  вокруг оси OX; б)  вокруг оси OY.

Вариант №2   Задание №1. Найти площадь фигуры, ограниченной линиями: а) ; б) ; в)   Задание №2.  Вычислить объем тела вращения, полученный при вращении кривой: а)  вокруг оси OX; б)  вокруг оси OY.

 

Контрольные вопросы (ответьте письменно):

1.    Запишите определение криволинейной трапеции.

2.    Запишите формулу для вычисления площади криволинейной трапеции, ограниченной кривой y=f(x) и осью OX, сделайте схематично рисунок.

3.    Запишите формулу для вычисления площади криволинейной трапеции, ограниченной кривыми y=f(x) и y=g(x), сделайте схематично рисунок.

4.    Запишите формулу для вычисления объема тела вращения вокруг оси OX, сделайте схематично рисунок.

5.    Запишите формулу для вычисления объема тела вращения вокруг оси OY, сделайте схематично рисунок.

 

6.