
Практическое занятие: Показательные неравенства.
Цель: освоить решение показательных неравенств .
1. Для того, чтобы освоить решение показательных неравенств необходимо:
1) знать и уметь решать показательные уравнения;
2) знать и уметь применять признак монотонности (возрастания и убывания) показательной функции;
3) уметь решать простейшие неравенства (линейные, квадратные)
- По первому пункту вы сдали зачёт – решение показательных уравнений освоили.
- По второму пункту мы проводили исследовательскую работу: строили графики показательных функций и обобщили признаки возрастания и убывания функций по их формулам.
- Повторением способов решения простейших линейных и квадратных неравенств,; правил, связанных с решением неравенств, мы будем заниматься сегодня.
2. Познакомьтесь с материалом, вспомните или изучите решение простейших линейных неравенств, сделайте конспект и выполните самостоятельную работу,
Материал для повторения:
1) Изображение, обозначение числовых промежутков.

2) Правила преобразования неравенств, приводящие к равносильным неравенствам.

3). Запишите примеры решения линейных неравенств.


4). Решите самостоятельно неравенства:
Реши неравенства:
а) 2х ≥ 18
б) -4х > 16
в) 17х-2 ≤ 12х-1
г) 3(3х-1) > 2(5х-7)
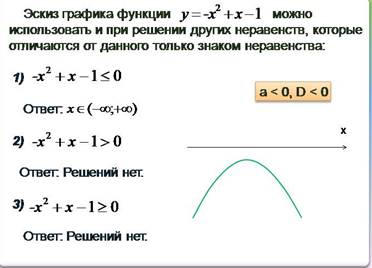
3. Познакомьтесь с материалом, вспомните или изучите решение простейших квадратных неравенств, сделайте конспект и выполните самостоятельную работу.
Материал для повторения:

|
|
|
|
|
|
|
|
|
Решите самостоятельно неравенства:
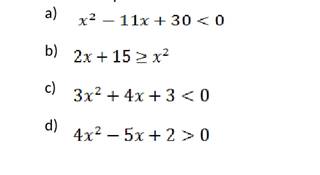
4.Повторите свойство показательных функций на возрастание и убывание (монотонность).
|
|
Укажите из перечисленных показательных функций возрастающие и убывающие: y = 4х y = Пх y = 0,5х y = 46х y = 18х y = 0,9х y = 0,00001х y
=(
|
5.Решение показательных неравенств.
Метод приведения к одному основанию.
Пример 1. Решить неравенство: ![]()
Перепишем неравенство: ![]() ;
;
![]() ;
;
![]() . Т. к 2>1, то по свойству 1
знак остаётся прежним, т. е.
. Т. к 2>1, то по свойству 1
знак остаётся прежним, т. е. ![]() ⇒
⇒ ![]() . Ребята, важно отметить, что
ответ можно записать либо в виде неравенства, либо в виде промежутка. Запишем в
виде промежутка.
. Ребята, важно отметить, что
ответ можно записать либо в виде неравенства, либо в виде промежутка. Запишем в
виде промежутка.
Ответ: х €![]() )
)
Метод вынесения общего множителя за скобки.
Пример 2. Решить неравенство: ![]() .
.
Потому что за скобки выносится наименьшая степень.
![]() ;
;![]() ;
; ![]() (т. к 2>1, то по свойству 1
знак остаётся прежним)
(т. к 2>1, то по свойству 1
знак остаётся прежним)
![]()
![]()
![]() .
.
Ответ: ![]() .
.
Метод введения новой переменной.
Пример 3. Решить неравенство: ![]() .
.
Здесь, как вы видите, лучше использовать Пусть ![]() ⇒
⇒ ![]() .
.
У нас получилось квадратное неравенство.
Для начала найдём корни, т.е. от неравенства перейдём к уравнению:![]() ⇒
⇒![]() .
.
Отмечаем их на числовой прямой, у нас получилось ![]() ⇒
⇒
1) Неравенство ![]() –решений
не имеет, т.к. корень
–решений
не имеет, т.к. корень ![]() не
удовлетворяет нашему условию
не
удовлетворяет нашему условию ![]() ;
;
2) ![]() , т.к. 3>1⇒
, т.к. 3>1⇒![]() .
.
Ответ: ![]()
Решите самостоятельно неравенства:
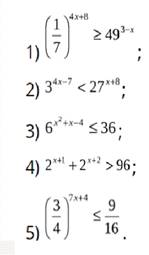
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.