
Практическое занятие № 21
Тема: «Изображение комбинационных устройств в микросхемах -демультиплексоры»
Цель: изучить различные микросхемы, использующие демультиплексоры, спроектировать схемы на этих микросхемах
Теория
Демультиплексор — это комбинационная схема, которая выполняет обратную операцию мультиплексора. Он имеет один вход, n строк выбора и максимум 2 n выходов. Вход будет подключен к одному из этих выходов на основе значений линий выбора.
Так как есть n строк выбора, будет 2 n возможных комбинаций нулей и единиц. Таким образом, каждая комбинация может выбрать только один выход. De-Multiplexer также называется De-Mux .
1×4 De-Multiplexer
1×4 De-Multiplexer имеет один вход I, две строки выбора, s 1 и s 0 и четыре выхода Y 3 , Y 2 , Y 1 и Y 0 . Блок-схема демультиплексора 1×4 показана на следующем рисунке.
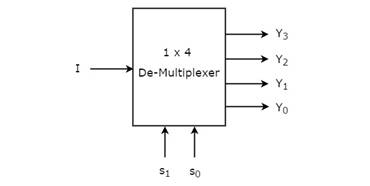
Рисунок 1 – Блок-схема демультиплексора
Мы можем реализовать эти булевы функции с помощью инверторов и вентилей с 3 входами И. Принципиальная схема демультиплексора 1×4 показана на следующем рисунке.
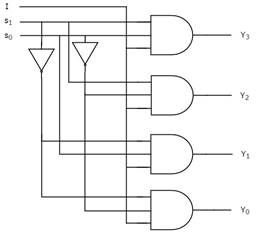
Рисунок 2 – Принципиальная схема демультиплексора
Реализация демультиплексоров высшего порядка
Теперь давайте реализуем следующие два демультиплексора высшего порядка, используя демультиплексоры низкого порядка.
· 1×8 демультиплексор
· 1×16 демультиплексор
1×8 демультиплексор
В этом разделе мы реализуем демультиплексор 1×8, используя демультиплексоры 1×4 и демультиплексор 1×2. Мы знаем, что 1×4 De-Multiplexer имеет один вход, две строки выбора и четыре выхода. Принимая во внимание, что демультиплексор 1×8 имеет один вход, три линии выбора и восемь выходов.
Итак, нам нужны два 1×4 демультиплексора на втором этапе, чтобы получить последние восемь выходов. Поскольку количество входов на втором этапе равно двум, нам требуется 1×2 демультиплексора на первом этапе, чтобы выходы первого этапа были входами второго этапа. Вход этого демультиплексора 1×2 будет общим входом демультиплексора 1×8.
Пусть демультиплексор 1×8 имеет один вход I, три линии выбора s 2 , s 1 и s 0 и выходы с Y 7 по Y 0 . Таблица истинности демультиплексора 1×8 показана ниже.
|
Выбор входов |
Выходы |
|||||||||
|
с 2 |
с 1 |
с 0 |
Y 7 |
Y 6 |
Y 5 |
Y 4 |
Y 3 |
Y 2 |
Y 1 |
Y 0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Мы можем легко реализовать демультиплексор 1×8, используя мультиплексоры низкого порядка, рассмотрев приведенную выше таблицу истинности. Блок-схема демультиплексора 1×8 показана на следующем рисунке.
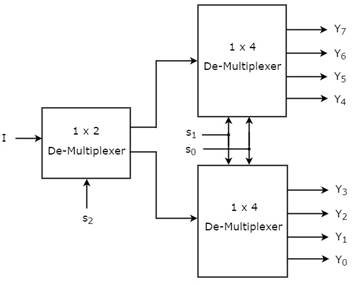
Рисунок 3 – Блок-схема демультиплексора1×8
Общие строки выбора s 1 & s 0 применяются к обоим демультиплексорам 1×4. Выходы верхнего демультиплексора 1×4 — от Y 7 до Y 4, а выходы нижнего демультиплексора 1×4 — от Y 3 до Y 0 .
Другая строка выбора s 2 применяется к демультиплексору 1×2. Если s 2 равно нулю, то один из четырех выходов нижнего демультиплексора 1×4 будет равен входу I, основываясь на значениях линий выбора s 1 & s 0 . Аналогично, если s 2 равен единице, то один из четырех выходов верхнего демультиплексора 1×4 будет равен входу I, основываясь на значениях линий выбора s 1 & s 0 .
1×16 демультиплексор
В этом разделе мы реализуем демультиплексор 1×16, используя демультиплексоры 1×8 и демультиплексор 1×2. Мы знаем, что 1×8 De-Multiplexer имеет один вход, три линии выбора и восемь выходов. Принимая во внимание, что демультиплексор 1×16 имеет один вход, четыре строки выбора и шестнадцать выходов.
Итак, нам нужны два демультиплексора 1×8 на втором этапе, чтобы получить окончательные шестнадцать выходов. Поскольку количество входов на втором этапе равно двум, нам требуется 1×2 демультиплексора на первом этапе, чтобы выходы первого этапа были входами второго этапа. Вход этого демультиплексора 1×2 будет общим входом демультиплексора 1×16.
Пусть демультиплексор 1×16 имеет один вход I, четыре строки выбора s 3 , s 2 , s 1 & s 0 и выходы Y 15 — Y 0 . Блок-схема демультиплексора 1×16 с использованием мультиплексоров более низкого порядка показана на следующем рисунке.
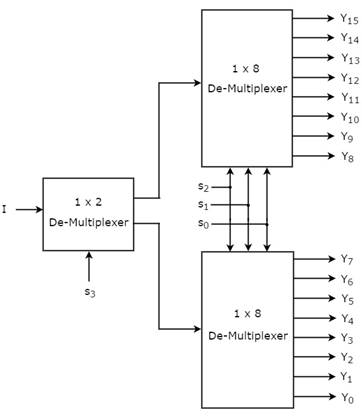
Рисунок 4 – Блок-схема демультиплексора1×16
Общие строки выбора s 2 , s 1 & s 0 применяются к обоим демультиплексорам 1×8. Выходы верхнего демультиплексора 1×8 — от Y 15 до Y 8, а выходы нижнего демультиплексора 1×8 — от Y 7 до Y 0 .
Другая строка выбора, s 3 , применяется к демультиплексору 1×2. Если s 3 равно нулю, то один из восьми выходов нижнего демультиплексора 1×8 будет равен входу I, основываясь на значениях линий выбора s 2 , s 1 & s 0 . Аналогично, если s3 равен единице, то один из 8 выходов верхнего демультиплексора 1×8 будет равен входу I, основываясь на значениях строк выбора s 2 , s 1 & s 0 .
Ход работы
1. Начертить временные диаграммы работы демультиплексора, изображённого на рисунке 1 (в тетради).
2. Используя каскадное включение демультиплексоров, для наращивания числа выходов, синтезировать демультиплексор с 16 выходами (1 → 16) на основе демультиплексоров с 4 выходами (1 → 4).
Изобразить эскиз в тетради и схему на А4 формате.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.