Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования и науки Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое пособие

для проведения

практического занятия

на тему:

«РАЗМЕРЫ ИЗОБРАЖЕНИЙ, ПРИНЦИП ИХ НАНЕСЕНИЯ НА ЧЕРТЕЖ ПО ГОСТ»

по дисциплине: «Инженерная графика»

для студентов 2 курса

спец. 15.02.01, 15.02.05, 19.02.03, 19.02.06, 19.02.08, 19.02.09

очного и заочного отделения

Разработал преподаватель: Е.В. Игнатова

2016

1 ЦЕЛЬ РАБОТЫ:

1.1 Получить сведения о нанесении размеров на чертежах.

1.2 Выполнить изображения вала, ролика и пластины и нанести их размеры.

2 ОБЩИЕ СВЕДЕНИЯ

2.1 Нанесение размеров на чертежах

Правила нанесения размеров на чертежах установлены ГОСТ 2.307-68. Основанием для определения действительных размеров изображенного на чертеже изделия и его элементов служат размерные числа, нанесенные на чертеже. Линейные размеры на чертеже указывают в миллиметрах без обозначения единицы измерения. В случае если размеры указываются в технических требованиях или пояснительных надписях на чертеже, единицы измерения указывают обязательно.

При необходимости указания линейных размеров в других единицах измерения (см, м) их указывают сразу после размерного числа, или оговаривают это в технических требованиях на чертеже. Угловые размеры на чертеже указывают в градусах, минутах и секундах с обозначением единицы измерения, например, 15°; 15°40′; 15°40′30′′.     Количество размеров должно быть минимальным. На чертеже указывают ровно столько размеров, сколько необходимо, чтобы метрически полно определить соответствующие размеры (длину, ширину, высоту, диаметр или радиус и т. д.) каждого элемента детали и их относительное расположение. Размеры на чертеже должны быть проставлены геометрически полно и технологически грамотно, они обязательно должны согласовываться с производственным процессом, типичным для изготовления данной детали (разметка, обработка, контроль).

Для нанесения размеров на чертеже проводят выносные и размерные линии и указывают размерные числа. Размерные линии с обоих концов ограничивают стрелками: внутри, снаружи, с одной стороны (при недостатке места для их простановки, стрелки могут заменяться засечками или четкими точками). Обобщенно эти правила показаны на рис.1

При нанесении размера прямолинейного отрезка (рис.1, а) размерную линию проводят параллельно этому отрезку, а выносные линии – перпендикулярно размерным. Так наносят линейные размеры деталей на чертежах. Размеры радиусов и диаметров на окружностях наносят так, как показано на рис.1 б, в.

Размер стрелок зависит от толщины линий видимого контура и должен быть одинаков для всех размеров данного чертежа. На строительных чертежах вместо стрелок допускается применять засечки на пересечении размерных и выносных линий.

ГОСТ 2.307-68 устанавливает форму и размеры стрелок и засечек, минимальные расстояния от контура изображения детали до первой размерной линии и между соседними размерными линиями.

Стандартом устанавливаются расстояния выхода выносных линий за размерную и размерной линии – за выносную, если вместо стрелок применяются засечки (рис.2). Размерные числа проставляют над размерной линией по возможности ближе к ее середине. При недостатке места над размерной линией для нанесения размерного числа его наносят на продолжении размерной линии или на полке линии-выноски (см. рис.1, а, б). При расположении линейных и угловых размеров с наклоном в пределах зон, указанных штриховкой на рис.2, размерные числа наносят на полках. Только на полках наносят и размеры малых углов, при любом их расположении. Размер шрифта для нанесения размеров принимают в зависимости от масштаба изображения и насыщенности чертежа, но не менее 2,5 мм для чертежей, выполненных тушью или чернилами, и не менее 3,5 мм – для чертежей, выполненных карандашом. Размерные числа и размерные стрелки не допускается пересекать линиями, в местах простановки размерных чисел и размерных стрелок любые линии необходимо прерывать (см. рис.2).

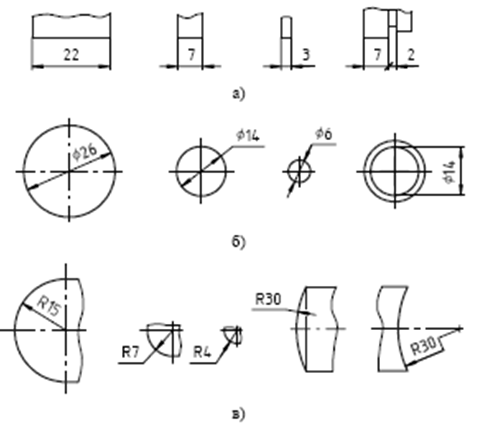
Рисунок 1

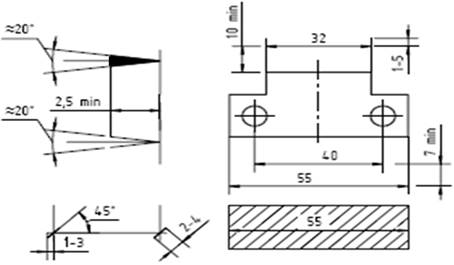Рисунок 2

Для сокращения количества изображений на чертеже, а также для удобства чтения чертежа стандартом предусмотрен ряд обозначений и условных знаков, применяемых при нанесении размеров.

При нанесении размера радиуса перед размерным числом помещают прописную букву R (см. рис. 1в). При указании размера диаметра во всех случаях перед размерным числом наносят знак «∅». Если необходимо проставить размер диаметра или радиуса сферы перед размерным числом также проставляют знак ∅ или R без надписи «Сфера» (рис. 3).

В случаях, когда на чертеже трудно отличить сферу от других поверхностей, перед знаком диаметра или обозначением радиуса допускается указывать слово «Сфера» или знак «Ò», например, «Сфера ∅25, ÒR16 (рис.3 б). Если элемент детали имеет форму квадрата, или его сечение является квадратом, то для нанесения их размеров применяется знак «􀀀» (рис.3 в, г).

Высота знака «􀀀» и диаметр знака «Ò» должны быть равны высоте размерных чисел на чертеже.

При нанесении размеров деталей, форма которых определена одним изображением, перед размерным числом, указывающим толщину детали, проставляется буква s, а перед числом, указывающим длину, – буква l (рис.3 в, д).

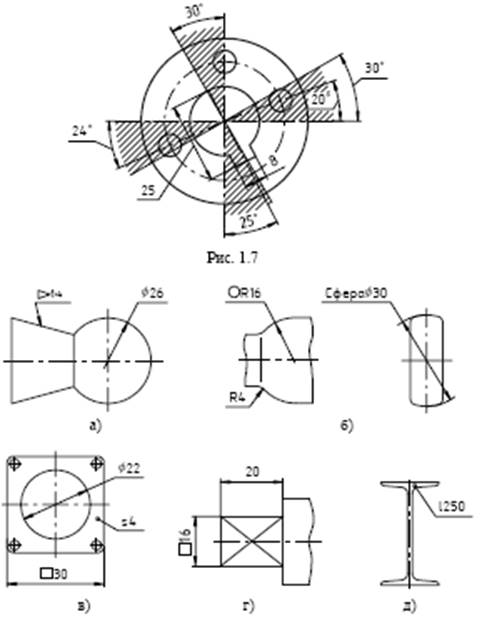
Рисунок 3

Для нанесения размеров конусности и уклона используются специальные знаки, размер, форма и варианты применения которых показаны на рис.4

Многие детали имеют фаски – поверхности, имеющие вид усеченного конуса или грани наклонной призмы. Если фаска выполнена под углом 45°, то ее размер указывают в виде произведения двух чисел, в котором первое число обозначает высоту фаски, а второе – величину угла (рис.5 а). Если фаска выполнена под углом, отличным от 45°, ее размер указывают по общим правилам (рис. 5б). Если деталь имеет несколько одинаковых элементов (отверстий, фасок и др., кроме скруглений), то на чертеже наносится размер одного элемента, а их общее количество указывают либо перед размерным числом, либо под ним – ниже размерной линии (рис.5 в).

Размеры одинаковых, повторяющихся на чертеже элементов (скруглений, уклонов и т.п.) многократно не повторяют, а дают в технических требованиях чертежа их общее обозначение по типу: «Неуказанные формовочные уклоны 5°» или «Неуказанные радиусы 2…3 мм».

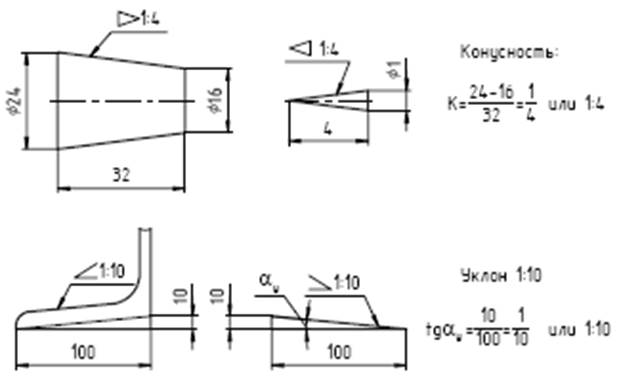
Рисунок 4

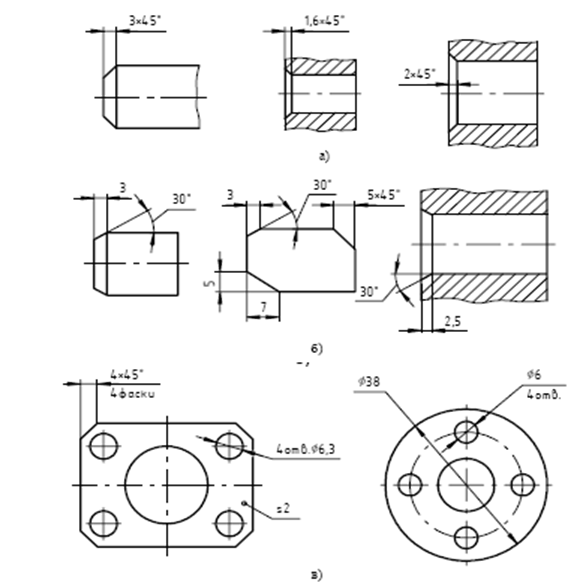Рисунок 5

ЗАДАНИЕ

Содержание задания. На листе чертежной бумаги формата А3 выполнить изображения вала, ролика и пластины и нанести их размеры. Вариант задания для каждой из деталей соответствует порядковому номеру фамилии студента в групповом журнале и выбирается по таблицам

         Задание выполнить в масштабе 1:1. Толщину пластин принять равной 4 мм.

Методические указания к выполнению задания. Для выполнения задания необходимо изучить ГОСТ 2-307-68 – нанесение размеров и предельных отклонений, повторить ГОСТ 2.303-68* – линии чертежа. На каждом из рисунков таблиц приведены определяющие размеры деталей в натуральную величину. По этим размерам рассчитывают коэффициент искажения изображения детали на рисунке и используют для пропорционального увеличения ее изображения на чертеже.

Образец выполнения задания приведен на рис.6

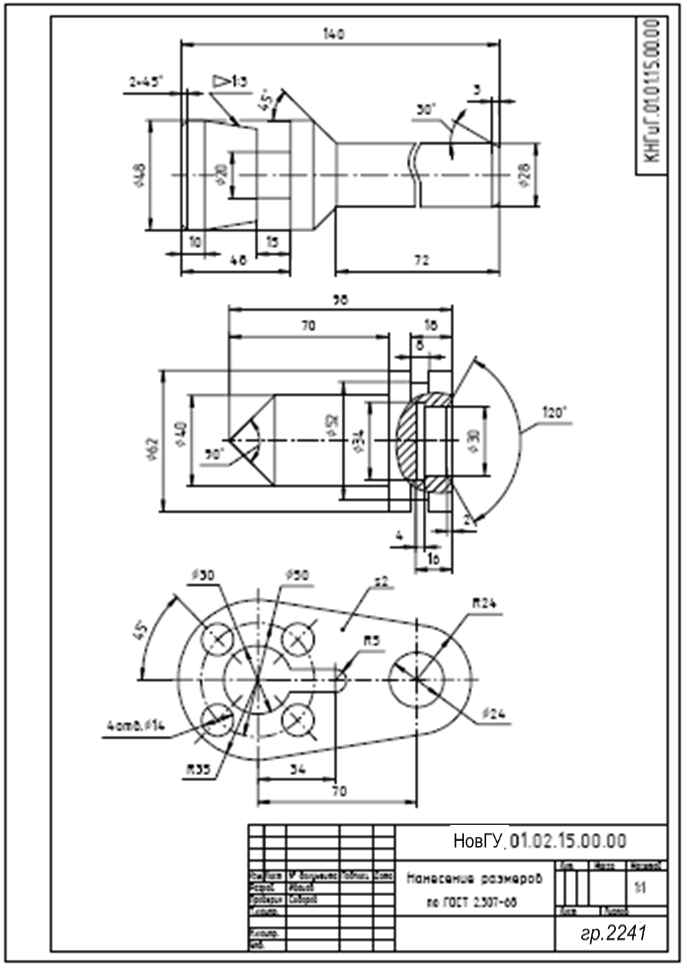
Рисунок 6

Варианты заданий

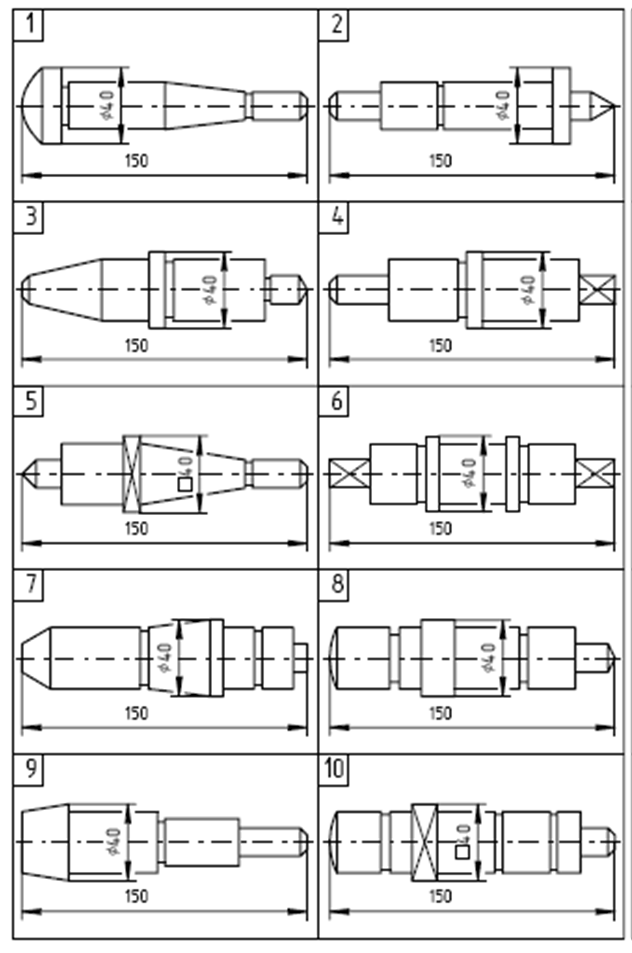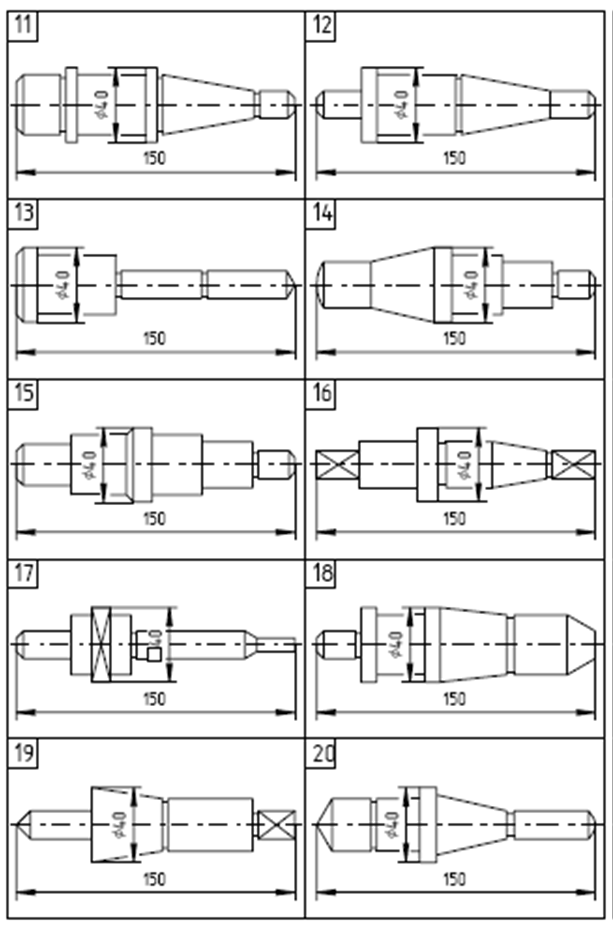
Варианты заданий

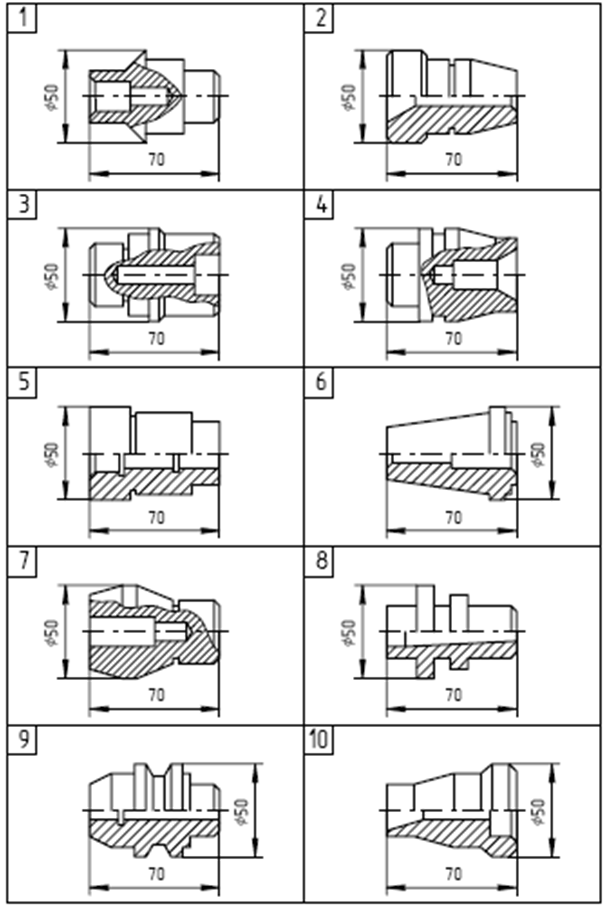
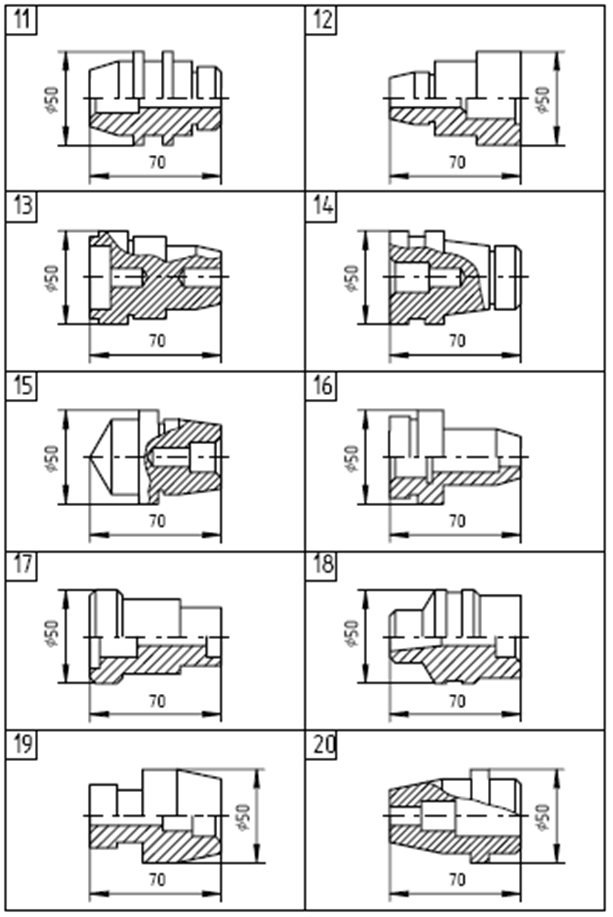
Варианты заданий

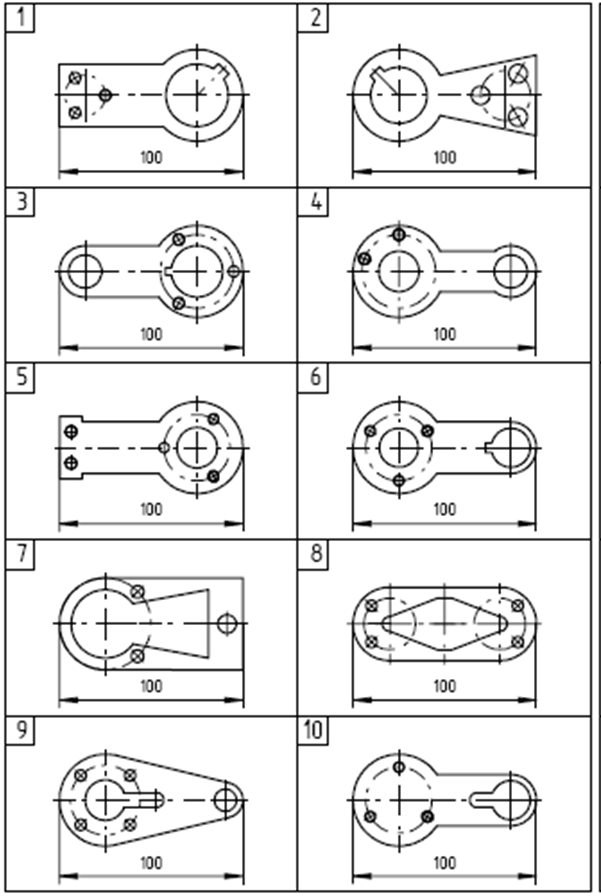
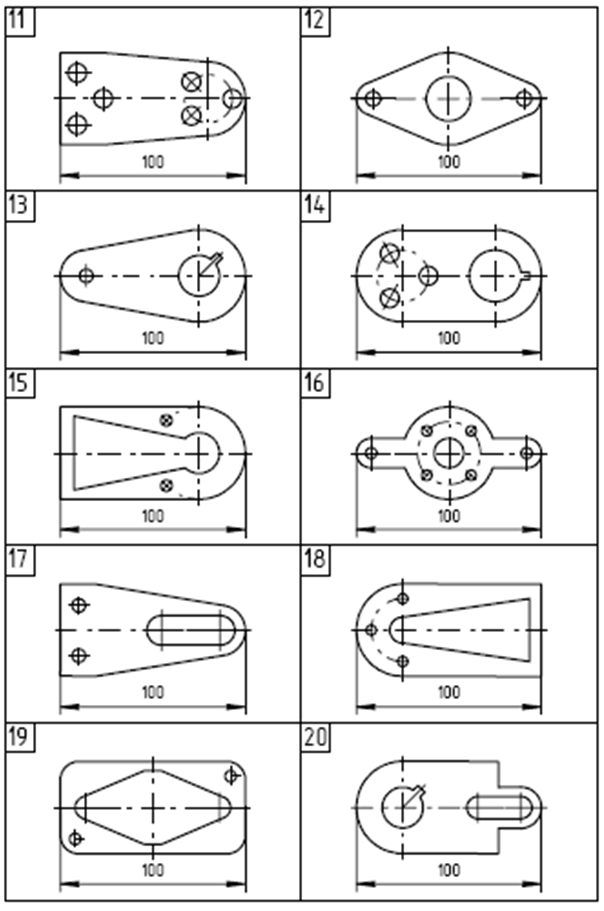
Деление окружности на равные части

Деление окружности на три равные части (рис. а).   

Деление окружности на три равные части выполняем с помощью циркуля. Из лежащей на окружности точки А как из центра проводим дугу. Радиус R  дуги  равен  радиусу  заданной  окружности. Дуга пересекает  окружность в точках 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.             

Деление окружности на шесть равных частей (рис.  б).

Из  центров  в  точках 1  и 4  раствором  циркуля,  равным  радиусу  заданной  окружности R,  проводим  дуги.  Точки 1, 2, 3, …, 6  делят  окружность на шесть равных частей.

Деление окружности на двенадцать равных частей  (рис. в).

Из центров в точках 1, 4, 7, 10 раствором циркуля, равным радиусу заданной окружности R, проводим дуги. Точки 1, 2, 3,…, 12 делят  заданную окружность на двенадцать равных частей.

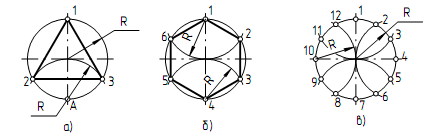
Рис. 1.19

Деление окружности на четыре и восемь равных частей (рис. а).

Взаимно  перпендикулярные  центровые  линии  АС  и BD  делят  окружность на четыре равные части.  Для того чтобы разделить окружность на восемь равных частей, проводим  биссектрисы  углов АОВ  и ВОС.  Точки 1, 2, 3,…, 8  делят  окружность на восемь равных частей.

Деление окружности на пять равных частей (рис. б).

Из центра А раствором циркуля, равным радиусу заданной окружности R, проводим дугу, которая пересекает окружность в точках В и С. Отрезок ВС делит радиус окружности ОА на две равные части в точке D. Из центра D проводим дугу 1K радиусом R₁ (R₁ = 1D). Отрезок 1K есть сторона правильного пятиугольника. От точки 1 по заданной окружности откладываем хорды, которые равны отрезку 1K.

Деление окружности на семь равных частей (рис. в).

Из центра А раствором циркуля, равным радиусу заданной окружности R, проводим дугу, которая пересекает окружность в точках В и С. Отрезок ВС делит радиус окружности ОА на две равные части в точке D. От  точки 1  по  заданной  окружности  откладываем  хорды,  которые равны отрезку ВD, где BD – сторона правильного семиугольника.

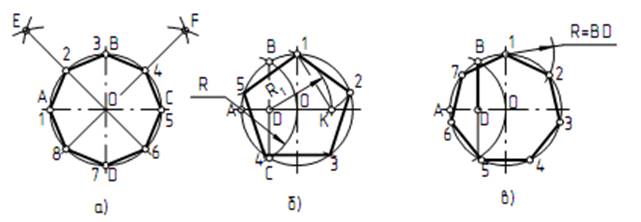
Рис.

Сопряжения

При выполнении геометрических построений часто приходится плавно соединять прямые и кривые линии. Плавный переход одной линии в другую называется сопряжением.

Для построения сопряжения необходимо знать величину радиуса сопряжения, найти центры и точки сопряжений. Элементы сопряжений показаны на рис.

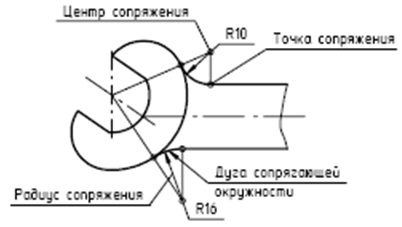
Дуга окружности, по которой одна линия плавно переходит в другую, называется дугой сопрягающей окружности.

Радиус этой окружности – радиус сопряжения. Центр этой окружности – центр сопряжения. Точка, в которой одна линия плавно переходит в другую, – точка сопряжения. Построение сопряжений рассмотрим на примере универсального «чертежа-справочника» (рис. ), при вычерчивании которого применены все основные виды сопряжений.

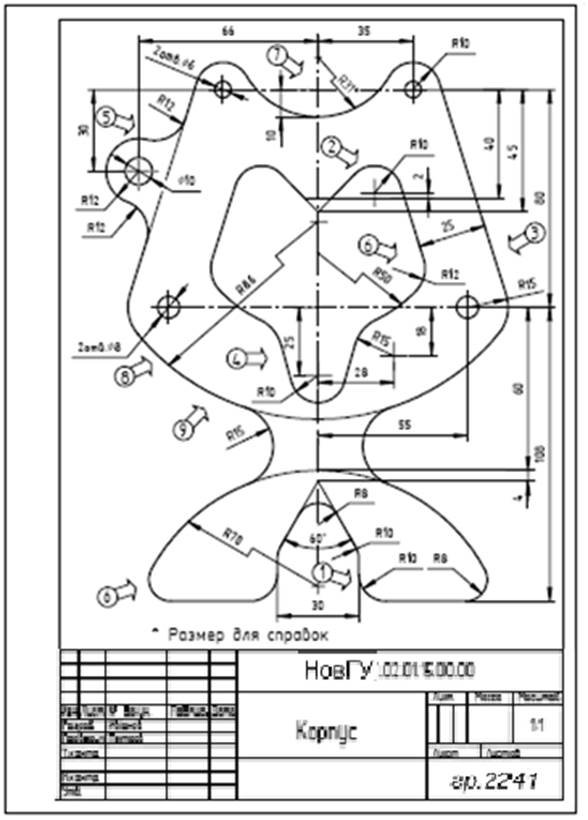
Использованные при построении чертежа виды сопряжений отмечены на нем пронумерованными стрелками, а на рис. показано подробное построение каждого из обозначенных сопряжений с последующим кратким описанием.

Сопряжение сторон острого и тупого углов дугой окружности заданного радиуса R1 (рис. а, б).

Расстояние от центра сопряжения до каждой стороны угла равно заданному радиусу сопряжения R1. Чтобы найти центр сопряжения, необходимо провести две вспомогательные прямые, параллельные каждой стороне угла, на расстоянии R1 от них. Для проведения вспомогательных прямых из произвольных точек, лежащих на сторонах угла, раствором циркуля, равным R1, выполняем две-три засечки и к ним проводим касательные.

Точка пересечения О построенных касательных и будет центром сопряжения. Точки сопряжения получим, опустив из точки О перпендикуляры к каждой стороне заданного угла.

Сопряжение сторон прямого угла дугой окружности заданного радиуса R1 (рис. в).

Из вершины прямого угла как из центра проводим дугу радиуса R1. Из точек пересечения построенной дуги со сторонами заданного угла как из центров выполняем две засечки радиусом R1. На пересечении засечек определяем точку О – центр сопряжения. Из него проводим дугу сопрягающей окружности.

Построение касательной к окружности (рис. а). Дана окружность радиуса R1 с центром в точке О1 и точка А, не принадлежащая окружности. Требуется через точку А провести касательную к заданной окружности. Соединяем точку А с центром заданной окружности О1. Отрезок О1А делим на две равные части – получаем точку В. Из центра В проводим дугу окружности. Её радиус R = АВ. На пересечении построенной дуги с заданной окружностью находим точку касания N. Через неё и точку А проводим касательную.

Построение касательной к двум окружностям (внешнее касание) (рис.б).

Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним внешнюю касательную. Из центра О2 проводим вспомогательную окружность радиуса (R2 – R1). Соединяем центры О1 и О2. Отрезок О1О2 делим на две равные части – получаем точку В. Из центра В проводим дугу окружности. Её радиус R = О2В. На пересечении дуги с вспомогательной окружностью получаем точку N. Через центр О2 и точку N проводим прямую. Её пересечение с окружностью радиуса R2 даст нам первую точку касания М. Через центр О1 проводим отрезок О1K параллельно О2М. Точка K – вторая точка касания. Соединяем точки K и М. Прямая МK есть внешняя касательная к заданным окружностям.

Построение касательной к двум окружностям (внутреннее касание) (рис. в).

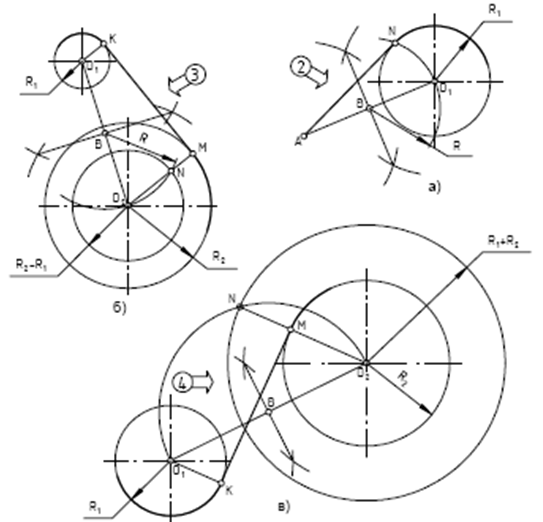
Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним внутреннюю касательную. Из центра О2 проводим вспомогательную окружность радиуса (R2 + R1). Соединяем центры О1 и О2. Отрезок О1О2 делим на две равные части – получаем точку В. Из центра В проводим дугу окружности. Её радиус R = О2В. На пересечении дуги с вспомогательной окружностью получаем точку N. Через центр О2 и точку N проводим прямую, её пересечение с окружностью радиуса R2 даст нам первую точку касания М. Через центр О1 проводим отрезок О1K параллельно О2М. Точка K – вторая точка касания. Соединяем точки K и М. Прямая МK есть внутренняя касательная к заданным окружностям.

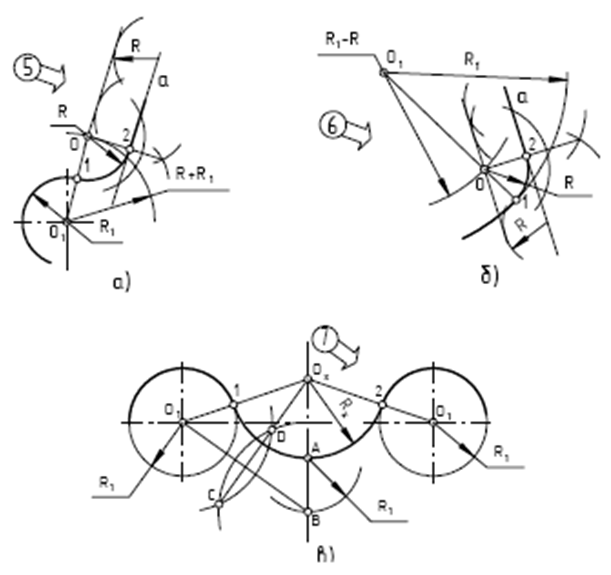
Построение внешнего сопряжения дуги и прямой дугой радиуса R (рис. а).

Даны дуга окружности радиуса R1 с центром в точке О1 и прямая а. Из центра О1 проводим вспомогательную дугу радиуса (R + R1). Проводим вспомогательную прямую, параллельную заданной прямой а, на расстоянии радиуса сопряжения R. На пересечении вспомогательных дуги и прямой получаем точку О – центр сопряжения. Проводим прямую ОО₁ – получаем первую точку сопряжения. Опускаем перпендикуляр из точки О на прямую а – получаем вторую точку сопряжения. Проводим сопрягающую дугу радиуса R от первой до второй точки сопряжения.

Построение внутреннего сопряжения дуги и прямой дугой радиуса R (рис.б).

Даны дуга окружности радиуса R1 с центром в точке О1 и прямая а. Из центра О₁ проводим вспомогательную дугу радиуса (R1 – R). Проводим вспомогательную прямую, параллельную заданной прямой а, на расстоянии радиуса сопряжения R. На пересечении вспомогательных дуги и прямой получаем точку О – центр сопряжения. На продолжении прямой ОО₁ получаем первую точку сопряжения. Опускаем перпендикуляр из точки О на прямую а. Получаем вторую точку сопряжения. Проводим сопрягающую дугу радиуса R от первой до второй точки сопряжения.

Построение сопряжения двух дуг окружностей дугой, проходящей через заданную точку (внешнее касание) (рис. в).

Даны две симметрично расположенные окружности радиуса R₁ с центрами в точках О₁ и точка А, через которую должна пройти неизвестная дуга сопряжения Rx. Из точки А как из центра проводим дугу радиуса R₁. На пересечении дуги с осью симметрии получаем точку В. Соединяем прямой точки В и О₁. Из точек В и О₁ как из центров проводим дуги произвольного радиуса, но большего, чем половина отрезка ВО₁, – получаем точки С и D. Через точки С и D проводим прямую. На пересечении прямой СD c осью симметрии находим

центр сопряжения Оx. Соединяем точку Оx с точками О₁. Пересечение отрезков ОxO₁ c заданными дугами окружностей даст нам точки сопряжения 1 и 2. Проводим дугу радиуса Rx из центра Оx от точки 1 к точке 2.

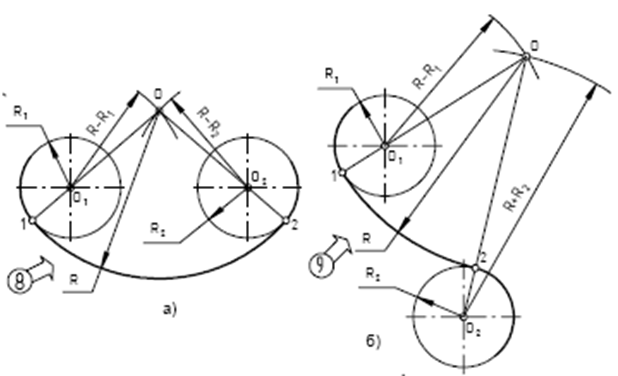
Построение внутреннего сопряжения дуг двух окружностей дугой радиуса R (рис. а).

Даны две окружности с центрами в точках О1 и О2. Их радиусы R1 и R2. Требуется провести к ним сопрягающую дугу радиуса R c внутренним касанием. Проводим вспомогательную дугу радиуса (R – R1) из центра О1 и дугу радиуса (R – R2) из центра О2. Получаем точку О – центр сопряжения. Проводим прямую ОО1 – получаем точку сопряжения 1. Проводим прямую ОО2 – получаем точку сопряжения 2. Проводим сопрягающую дугу радиуса R из

центра О от точки 1 до точки 2.

Построение смешанного сопряжения дуг двух окружностей дугой радиуса R (рис. б).

Даны две окружности с центрами в точках О1 и О2. Их радиусы R₁ и R₂. Требуется провести к ним сопрягающую дугу радиуса R cо смешанным касанием. Проводим вспомогательную дугу радиуса (R – R₁) из центра О₁ и дугу радиуса (R + R₂) из центра О₂ – получаем точку О (центр сопряжения). Проводим прямую ОО1 – получаем точку сопряжения 1. Проводим пря-

мую ОО₂ – получаем точку сопряжения 2. Проводим сопрягающую дугу радиуса R из центра О от точки 1 до точки 2.

ЗАДАНИЕ 2

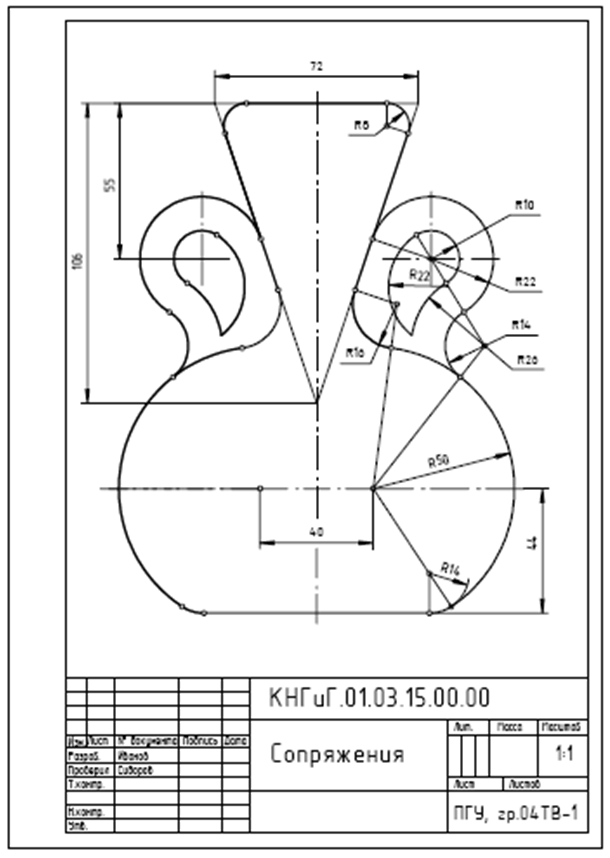
СОПРЯЖЕНИЯ

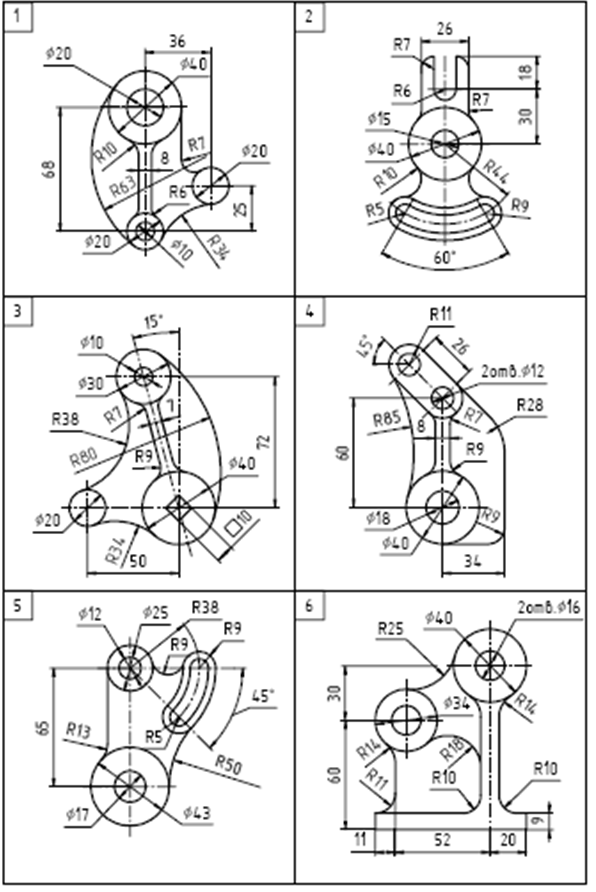
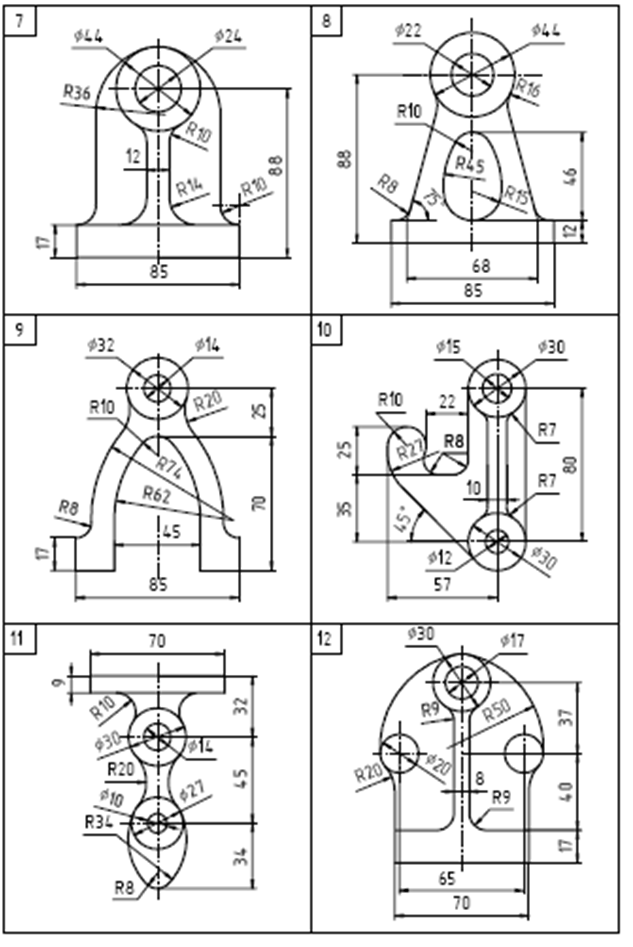
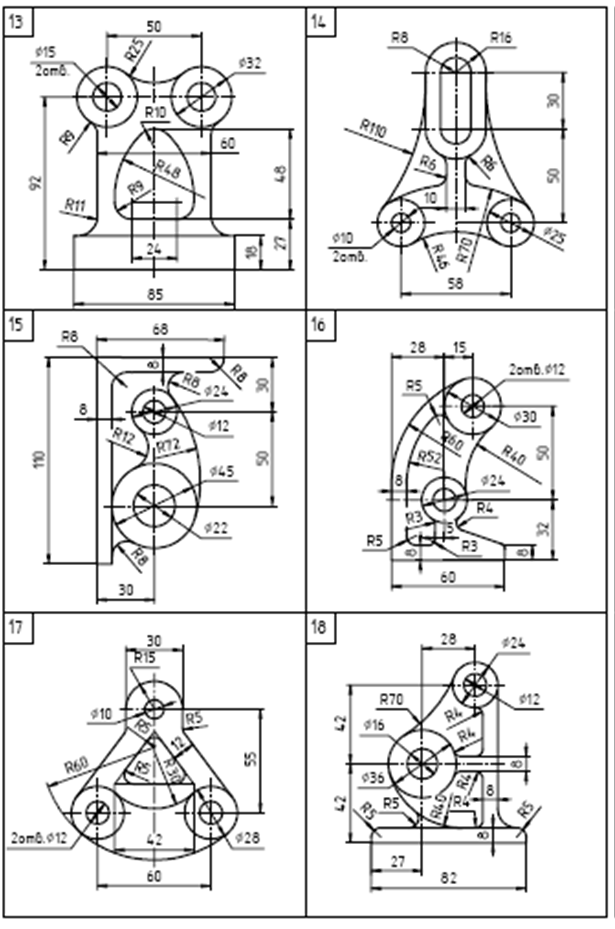
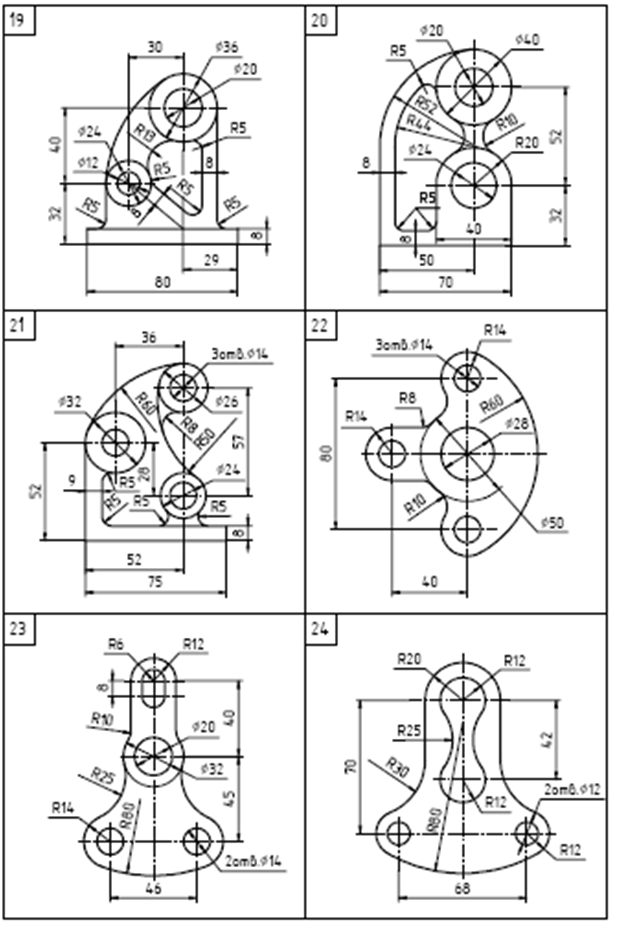
Содержание задания. На листе чертежной бумаги формата А4 или А3 вычертить контур технической детали с построением сопряжений и других геометрических построений. Нанести размеры. Вариант задания соответствует порядковому номеру фамилии студента в групповом журнале и выбирается по табл. Масштаб изображения при выполнении задания выбрать самостоятельно в зависимости от размеров технической детали и размеров используемого формата.

Методические указания к выполнению задания. Приступая к выполнению чертежа, необходимо:

- изучить тему «Геометрические построения на чертежах»;

- из табл.  по своему порядковому номеру в журнале группы вы-

брать вариант;

- произвести анализ графического состава предложенного для построения контура, т.е. определить, какие геометрические построения необходимо применить в данном случае и разбить их на отдельные этапы. Все построения вначале выполняются тонкими линиями, а затем контуры элементов детали обводятся сплошной толстой основной линией. Геометрические построения на чертеже можно не сохранять. Точки сопряжения необходимо сохранить обязательно в виде окружностей радиусом 0,6…1,0 мм.

Образец выполнения задания приведен на рис.

Варианты заданий