Практическая работа специальности 15.02.05. «Техническая эксплуатация оборудования в торговле и общественном питании»

Министерство образования и науки Краснодарского края

Государственное бюджетное профессиональное образовательное учреждение

Краснодарского края

«Армавирский механико – технологический техникум»

Методическое  пособие

для проведения

практического занятия

на тему:

«РАСЧЕТ  НА  ПРОЧНОСТЬ  ПРИ  ИЗГИБЕ»  

по дисциплине: «Техническая механика»

для студентов 2 курса 

спец.  15.02.01

очного отделения

Разработал преподаватель: Е.В. Игнатова

2016

1 ЦЕЛЬ РАБОТЫ

Знать:

- знать распределение нормальных напряжений по сечению балки при чистом изгибе, расчетные формулы и условия прочности;

Уметь:

- строить эпюры поперечных сил и изгибающих моментов;

- выполнять проектировочные и проверочные расчеты на прочность.

2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:

- изучить теоретический материал с помощью  методического пособия;

- по варианту задания выполнить расчеты на прочность и построить эпюры поперечных сил и изгибающих моментов;

- ответить на контрольные вопросы.

3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

3.1 Правила построения эпюр

1. Для участка, где отсутствует распределенная нагрузка, поперечная сила постоянна, а изгибающий момент меняется по линейному закону.

2. В частном случае, когда поперечная сила на участке равна нулю, изгибающий момент постоянен (чистый изгиб), график — пря­мая линия, параллельная продольной оси.

3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов — излом.

4. В сечении, где к балке приложена пара сил (сосредоточенный момент), на эпюре М_и возникает скачок на величину момента этой пары. Поперечная сила при этом не изменяется.

5. В сечении на конце балки поперечная сила равна приложенной в этом сечении сосредоточенной силе или реакции в заделке.

6.  На свободном конце балки или шарнирно опертом конце мо­мент равен нулю, за исключением случаев, когда в этом сечении приложена пара сил (внешний момент).

3.2 Расчетные формулы при изгибе

Распределение нормальных и касательных напряжений при изгибе

  где М_и — изгибающий момент в сечении;

у — расстояние до нейтраль­ного слоя;

J_х — осевой момент инерции сечения (чертеж 1);

Чертеж 1

         Q — поперечная сила в сечении;

          А — площадь сечения.

W_x— осевой момент сопротивления сечения;

Условие прочности при изгибе

где   — допускаемое напряжение.

Знаки изгибающих моментов и поперечных сил (чертеж 2)

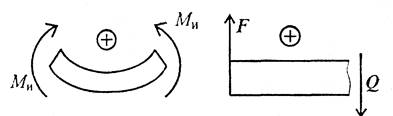
Чертеж 2

4 ПРИМЕР  ВЫПОЛНЕНИЯ  ЗАДАНИЯ

 На двухопорную балку действуют сосредоточенные силы и моменты (чертеж 3), определить реакции в опо­рах. Найти максимальный изгибающий момент и, используя усло­вие прочности, подобрать необходимые размеры поперечных сече­ний. Материал — сталь, допускаемое напряжение изгиба σ =160 МПа. Сечение — швеллер. Построить эпюры поперечных сил и изгибающих моментов.

Решение:

Для двухопорной балки построение эпюр начинают с определе­ния опорных реакций балки. Для их определения использовать систему  уравнений равновесия, составить два уравнения моментов относи­тельно шарнирных опор. Затем произвести проверку правильности решения по уравнению ∑F_nу = 0.

1. Определение реакций в опорах. Уравнения равновесия:

∑ m _А=0;

-F₁• 6 + m - R_В • 10 + F₂• 12  = 0;

-35 • 6 + 80 - R_В • 10 + 70 -12 = 0;

R_В • 10 = -210 + 80 + 840;

R_В = 71 кН.

∑ m _В = 0;

R_А • 10 + F₁ • 4 + m + F₂ • 2 = 0;

R_А • 10 + 80 + 35 • 4 + 70 • 2 = 0;

R_А • 10 = -80 - 140 - 140 = -360;

R_А=-36кН.

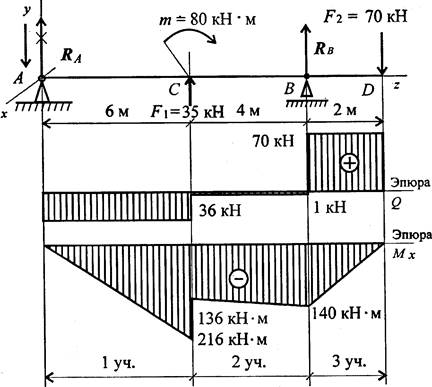
Чертеж 3

Реакция в опоре направлена в обратную сторону.

Проверка: ∑ F _у = 0;

- R_А + F₁ + R_В - F₂ = 0;

 -36 + 35 + 71 - 70 = 0.

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечны: сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр.

Участок 1 (от точки А до точки С).

В точке А приложена реакция R_А, направленная вниз. Поперечная сила на участке постоянна: Q₁=R_А = -36 кН.

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F₁= 35кН, напра­вленная вверх, — здесь возникнет скачок вверх на величину 35 кН. Момент в точке С (слева) может быть рассчитан по известной зави­симости М_с^слева = - R_А • 6;

М_с^слева = -36 • 6 = -216 кН м.

Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна Q_с= — R_А  + F₁;

Q_с = -36 + 35 = -1кН.

В точке С приложена внешняя пара сил с моментом 80 кНм, следовательно, здесь проявляется скачок на величину приложенного момента:

М_с^справа = М_с^слева + m;

М_с^справа = -216 + 80 = 136кН-м.

Поперечная сила на втором участке постоянна: Q₂ = Q_с^справа.

Момент в точке В определяется по зависимости

М_в =- R_А • 10 + F₁• 4 + т;

М_в = -36 • 10 + 35 • 4 + 80 = -140 кНм.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила R_В. Здесь появляется скачок на величину 71 кН, Q_В =-1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т.к. здесь не приложена внешняя пара сил: М_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.

По полученным значениям сил и моментов построить эпюры (эпю­ры под схемой вала, чертеж 3).

     3. Опасное сечение – сечение балки, где действует максимальный момент. Подобрать размеры балки в опасном сечении по условию прочности

;

;

мм³ 

или  W_x=135cм³

Основываясь на значении W_x=135cм³  по таблице ГОСТ 8240-89 выбрать швеллер №20;

момент сопротивления W_x=152cм^3;

площадь сечения  А=23,4 см²

5 ЗАДАНИЕ

Для двухопорной балки, нагруженной сосредоточен­ными силами и парой сил с моментом, определить реакции в опо­рах. Найти максимальный изгибающий момент и, используя усло­вие прочности, подобрать необходимые размеры поперечных сече­ний. Материал — сталь, допускаемое напряжение изгиба              σ =160 МПа. Сечение — швеллер.

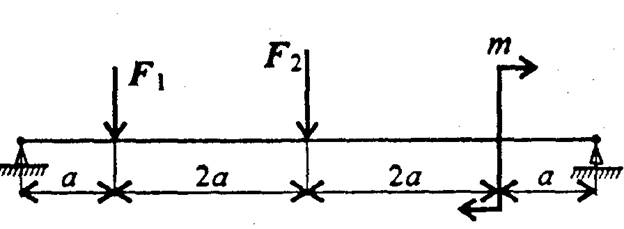
Рисунок 1

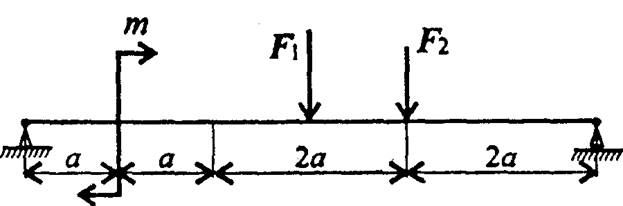
Рисунок 2

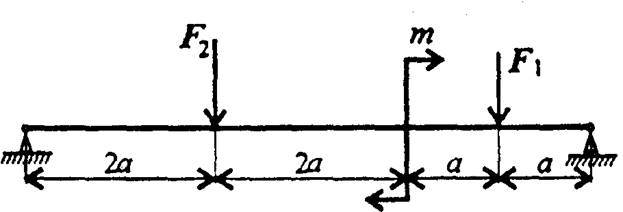
Рисунок 3

ВАРИАНТЫ  ЗАДАНИЙ

6 СПРАВОЧНЫЕ МАТЕРИАЛЫ 

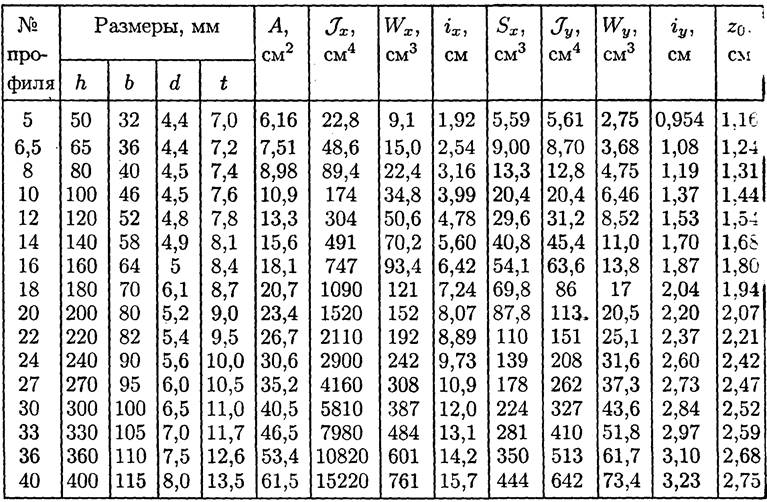
Сталь горячекатаная. ШВЕЛЛЕРЫ (по ГОСТ 8240-89)

 Обозначения:

h — высота швеллера;

Ь — ширина швеллера;

d — толщина стенки;

t — средняя толщина полки;

А — площадь швеллера;

J — момент инерции;

W — момент сопротивления;

i — радиус инерции;

S — статический момент полусечения;

z_о — расстояние от оси у до наружной грани стенки.

Таблица 1

7 КОНТРОЛЬНЫЕ    ВОПРОСЫ

1.     Какое условие прочности при изгибе?

2.     Чему равно допускаемое напряжение при изгибе?

3.     Какие правила построения эпюр вы знаете?

4.     Как определить наибольший изгибающий момент?

5.     По какому параметру подбирается швеллер?

ЛИТЕРАТУРА

1.     Олофинская В.П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий.- М.: ФОРУМ-ИНФРА-М, 2007.

2.     Мовнин М.С., Израелит А.Б., Рубашкин А.Г. Основы технической механики. - Л.: Машиностроение, 1982.

3.     Никитин Е.Н. Теоретическая механика.- М.: Высшая школа, 1983.

4.     Файн А.М. Сборник задач по теоретической механике.- М.: Высшая школа, 1987.