Практическая работа специальности 38.02.04.

Практическое занятие № 1

Тема: Действия над матрицами. Вычисление определителей матриц. Решение прикладных задач в области профессиональной деятельности.

Цель: закрепить практические навыки вычисления определителей и выполнения действий над матрицами, Решение прикладных задач в области профессиональной деятельности.

Наглядные пособия: учебники

Литература:

1. Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2019.

2. Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретическая часть

Определение матрицы

Матрицей размером $m\times n$ называется совокупность $m\cdot n$ чисел, расположенных в виде прямоугольной таблицы из строк и столбцов:

$A=(a_{ij}),~i=1,\ldots,m;~j=1,\ldots,n.$

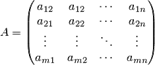
Числа, составляющие матрицу, называются элементами матрицы: $a_{ij}$ — элемент матрицы, стоящий на пересечении i-й строки и j-го столбца матрицы. Всюду далее предполагаются, что элементы матриц являются действительными числами, если не оговорено противное.

Пример. Определить размеры матриц

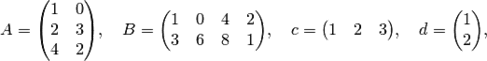Решение. Матрица имеет размеры $3\times 2$ , а матрица $B-2\times 4,~c-1\times 3,~d-2\times 1$ Две матрицы и называются равными , если они имеют одинаковые размеры $(m\times n)$ и равные соответствующие элементы: $a_{ij}=b_{ij},~i=1,\ldots,m;~j=1,\ldots,n$ .

Если у матрицы количество строк равно количеству столбцов , то матрицу называют квадратной (n-го порядка). Элементы $a_{11},a_{22},\ldots,a_{nn}$ образуют главную диагональ квадратной матрицы соединяющая левый верхний угол матрицы (элемент $a_{11}$ ) с правым нижним углом (элемент $a_{nn}$ )).

Действия над матрицами

1. Сумма матриц: А + В.

Складывать можно только матрицы одного размера. При сложении двух матриц одного размера получается матрица того же размера, элементы которой равны сумме элементов слагаемых матриц, стоящих на соответствующих местах.

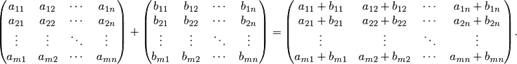
Нельзя, например, найти суммы вида

$\begin{pmatrix}1&2\\3&4\end{pmatrix}+\begin{pmatrix}5\\6\end{pmatrix}$ или $\begin{pmatrix}1&2\end{pmatrix}+\begin{pmatrix}3\\4\end{pmatrix}\!.$

Пример. Найти сумму двух матриц

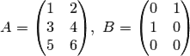$A=\begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}\!,~B=\begin{pmatrix}0&1\\1&0\\0&0\end{pmatrix}$ .

Решение. Складывая соответствующие элементы матриц, получаем

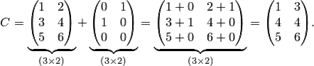
2. Умножение матрицы на число

При умножении числа на матрицу каждый ее элемент умножается на это число.

$c_{ij}=\lambda\,a_{ij},\quad i=1,\ldots,m;~j=1,\cdots,n.$

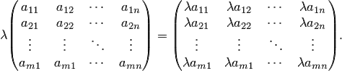
Пример. Найти произведение матрицы на число 2

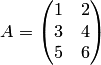
$A=\begin{pmatrix}1&2\\3&4\\5&6\end{pmatrix}$

Решение. Умножая на 2 каждый элемент матрицы , получаем

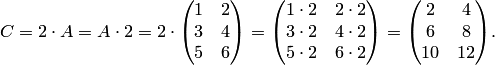
3. Умножение матриц :

Далеко не все матрицы можно перемножать.

Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B.

Таким образом, если порядок матрицы A равен m × p , то порядок согласованной с ней матрицы B должен быть равен p × n. Перемножать можно только согласованные матрицы (отметим, что квадратные матрицы одного порядка всегда согласованы).

Произведением двух согласованных матриц A (размера m × p) и B (размера
p × n ) называется матрица C (размера m × n) , элементы которой вычисляются по правилу: элемент матрицы С равен сумме попарных произведений элементов i-ой строки матрицы А и j-го столбца матрицы В:

Например, если требуется получить элемент c₂₁, то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы

Найдите все элементы матрицы С, которая получается при умножении матриц .

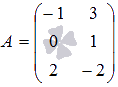
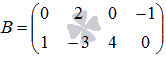
Порядок матрицы А равен p=3 на n=2, порядок матрицы В равен n=2 на q=4, следовательно, порядок порядок произведения этих матриц будет p=3 на q=4.

Последовательно принимаем значения i от 1 до 3 (так как p=3) для каждого j от 1 до 4(так как q=4), а n=2 в нашем случае, тогда

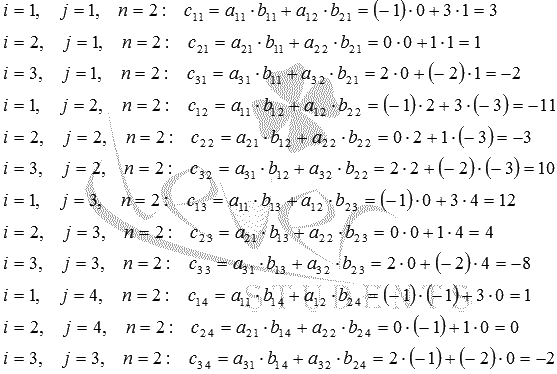
Так вычислены все элементы матрицы С, и матрица, полученная при умножении двух заданных матриц, имеет вид

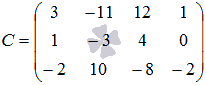
Пусть дана квадратная матрица:

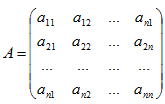
Определителем, соответствующим данной квадратной матрице А, называют число, обозначаемое символом:

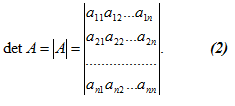
Определителем второго порядка называют число

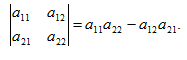
Пример

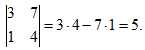
Определителем третьего порядка называют число

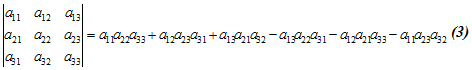
Чтобы запомнить, какие произведения в правой части равенства (3) берутся со знаком "+”, а какие со знаком "-”, полезно использовать следующее правило треугольников (правило Саррюса):

Пример :

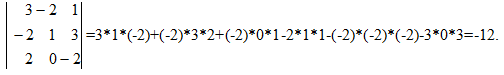
Для определителей справедливы следующие свойства:
1. Величина определителя не изменится, если его строки и столбцы поменять местами,

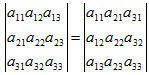Это свойство устанавливает равноправность строк и столбцов определителя. Поэтому следующие свойства действительны и для столбцов.

2. Определитель меняет свой знак на противоположный при перестановке двух столбцов (строк).

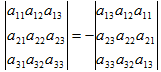
3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.
Пример :

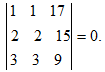
4. Общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак определителя.

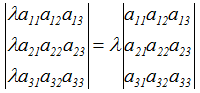
5. Если одна из строк (столбец) определителя состоит из нулей, то определитель равен нулю.

6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.
Пример :

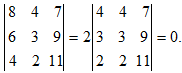
7. Если все элементы i-го столбца определителя представлены в виде суммы двух слагаемых: a_ij=b_ij+c_ij, i=l,n то определитель равен сумме двух определителей, у которых все столбцы, кроме i-го такие же, как и в заданном определителе, а i-й столбец в одном из слагаемых состоит из элементов b_ij , в другом – из элементов c_ij.

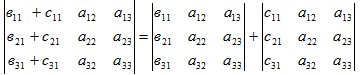
8. Определитель не меняется, если к элементам одной из его строк (столбцов) прибавляются соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Практическая часть

Вариант 1	Вариант 2
1. Сложить матрицы А и В:
А =, В = .	А= , В = .
2.Вычислить линейные комбинации матриц:
C=A+3B, если ,	C=2A-B, если , .
3.Найти произведение AB:
,	,
4.Вычислите определить
а) второго порядка б) третьего порядка	а) второго порядка 1. ; 2.; 3. ; б) третьего порядка 1.; 2. ; 3.

Практическое занятие № 1 Тема:

Умножение матрицы на число При умножении числа на матрицу каждый ее элемент умножается на это число

Последовательно принимаем значения i от 1 до 3 (так как p=3 ) для каждого j от 1 до 4 (так как q=4 ), а n=2…

Чтобы запомнить, какие произведения в правой части равенства (3) берутся со знаком "+”, а какие со знаком "-”, полезно использовать следующее правило треугольников (правило

Определитель не меняется, если к элементам одной из его строк (столбцов) прибавляются соответствующие элементы другой строки (столбца), умноженные на одно и то же число

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

26.11.2022