Практическая работа специальности 38.02.04.

Практическое занятие  № 8

Тема: Комплексные числа и действия с ними.

Цель: сформировать умение выполнять арифметические действия с комплексными числами.

Наглядные пособия: учебники

Литература:

1.     Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2019.

2.        Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретические сведения

Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i² = - 1.

Исходя из этого, получим следующее определение комплексного числа.

Определение. Комплексным числом называется выражение вида a + bi, где a и b - действительные числа. При этом выполняются условия:

а) Два комплексных числа a₁ + b₁i и a₂ + b₂i равны тогда и только тогда, когда a₁=a₂, b₁=b₂.

б) Сложение комплексных чисел определяется правилом:

(a₁ + b₁i) + (a₂ + b₂i) = (a₁ + a₂) + (b₁ + b₂) i.

в) Умножение комплексных чисел определяется правилом:

(a₁ + b₁i) (a₂ + b₂i) = (a₁a₂ - b₁b₂) + (a₁b₂ - a₂b₁) i.

3. Алгебраическая форма комплексного числа.

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0

Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.

Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.

Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

4. Действия над комплексными числами в алгебраической форме.

Над комплексными числами в алгебраической форме можно выполнять следующие действия.

1) Сложение.

Определение. Суммой комплексных чисел z₁ = a₁ + b₁i и z₂ = a₂ + b₂i называется комплексное число z, действительная часть которого равна сумме действительных частей z₁ и z₂, а мнимая часть - сумме мнимых частей чисел z₁ и z₂, то есть z = (a₁ + a₂) + (b₁ + b₂)i.

Числа z₁ и z₂ называются слагаемыми.

Комплексное число –a –bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z.

Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0

Пример 1. Выполните сложение (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Вычитание.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z, что z + z₂ = z₁.

Теорема. Разность комплексных чисел существует и притом единственна.

Пример 2. Выполните вычитание (4 – 2i) - (-3 + 2i).

(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.

3) Умножение.

Определение. Произведением комплексных чисел z₁=a₁+b₁i и z₂=a₂+b₂i называется комплексное число z, определяемое равенством: z = (a₁a₂ – b₁b₂) + (a₁b₂ + a₂b₁)i.

Числа z₁ и z₂ называются сомножителями.

Умножение комплексных чисел обладает следующими свойствами:

На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.

В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.

Пример 3. Выполните умножение (2 + 3i) (5 – 7i).

1способ(2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.

2 способ. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.

4) Деление.

Определение. Разделить комплексное число z₁ на комплексное число z₂, значит найти такое комплексное число z, что z · z₂ = z₁.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.

Пусть z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, тогда

.

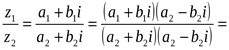
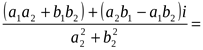
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.

Пример 4. Найти частное .

1 способ.

.

2 способ.

.

5) Возведение в целую положительную степень.

а) Степени мнимой единицы.

Пользуясь равенством i² = -1, легко определить любую целую положительную степень мнимой единицы. Имеем:

i³ = i² i = -i,

i⁴ = i² i² = 1,

i⁵ = i⁴ i = i,

i⁶ = i⁴ i² = -1,

i⁷ = i⁵ i² = -i,

i⁸ = i⁶ i² = 1 и т. д.

Это показывает, что значения степени iⁿ, где n – целое положительное число, периодически повторяется при увеличении показателя на 4 .

Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

Пример 5. Вычислите: (i ³⁶ + i ¹⁷) · i ²³.

i ³⁶ = (i ⁴)⁹ = 1⁹ = 1,

i ¹⁷ = i ^{4× 4+1} = (i ⁴)⁴× i = 1 · i = i.

i ²³ = i ^{4× 5+3} = (i ⁴)⁵× i³ = 1 · i³ = - i.

(i ³⁶ + i ¹⁷) · i ²³ = (1 + i) (- i) = - i + 1= 1 – i.

б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.

Пример 6. Вычислите: (4 + 2i)³

(4 + 2i)³ = 4³ + 3× 4²× 2i + 3× 4× (2i)² + (2i)³ = 64 + 96i – 48 – 8i = 16 + 88i.

Практическая часть

Вариант 1

1)     Решите уравнение: x²–24x+169=0.

2)     Вычислите: z₁+z₂; z₁–z_2; z₁·z₂; z₁:z₂ если, z₁=5–24i; z₂=25+7i

3)     Выполнить действия над комплексными числами

4)     Вычислите: i⁴²+i⁶³+5–36i.

Вариант 2

1)     Решите уравнение: x²–18x+106=0.

2)     Вычислите z₁+z₂; z₁–z_2; z₁·z₂; z₁:z₂ если, z₁=5–18i; z₂=25+4i

3)     Выполнить действия над комплексными числами

4)     Вычислите: i³³+i⁵¹+5–27i.

Вариант 3

1)     Решите уравнение: x²–14x+74=0.

2)     Вычислите z₁+z₂; z₁–z_2; z₁·z₂; z₁:z₂ если, z₁=5–14i; z₂=25+2i

3)     Выполнить действия над комплексными числами

4)     Вычислите: i²⁷+i⁴³+5–21i.

Контрольные вопросы:

1.      Какие числа называются комплексными?

2.      Как выполняются операции над комплексными числами?

3.      Модуль комплексного числа.

4.