Практическое решение геометрических задач.11 класс.

Практикум по теме «Площадь поверхности составного многогранника» 15 января 2020 г. 11 класс

Цель: практическое закрепление ЗУН.

Задачи из открытого банка задач.

1. Задание 8 № 25541

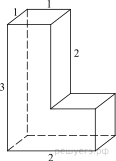Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей прямоугольников со сторонами 2, 1:

Ответ: 18.

2. Задание 8 № 25561

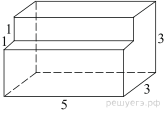Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 5 и двух площадей квадратов со стороной 1:

Ответ: 76.

3. Задание 8 № 25581

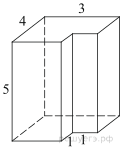Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух квадратов со стороной 1:

Ответ: 92.

4. Задание 8 № 25601

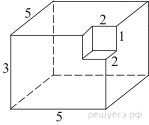Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:

Ответ: 110.

5. Задание 8 № 25621

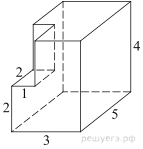Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:

Ответ: 94.

Примечание для тех, кто не верит в это решение.

Посчитайте площадь поверхности, сложив площади всех девяти граней данного многогранника, и смиритесь:

6. Задание 8 № 25641

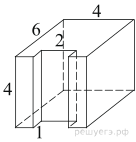Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 6, 4, 4 и двух прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников со сторонами 1 и 2:

Ответ: 132.

7. Задание 8 № 25661

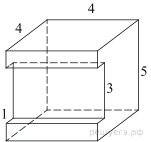Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 4, 4, 5 и двух прямоугольников со сторонами 1 и 4, уменьшенной на площадь двух прямоугольников со сторонами 1 и 3:

Ответ: 114.

8. Задание 8 № 25681

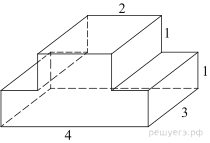Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей прямоугольников со сторонами 1, 3, 4 и 1, 2, 3, уменьшенной на удвоенную площадь прямоугольника со сторонами 2, 3:

Ответ: 48.

9. Задание 8 № 25701

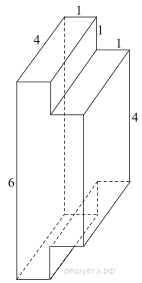
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4:

Ответ: 84.

Приведем другое решение

Площадь поверхности заданного многогранника равна площади прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади квадратов со стороной 1:

10. Задание 8 № 25721

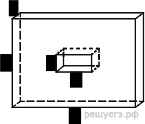Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:

Ответ: 96.

11. Задание 8 № 25881

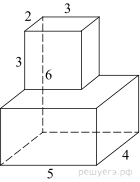Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов со сторонами 2, 3, 3 и 5, 4, 3 уменьшенной на удвоенную площадь прямоугольника со сторонами 3, 2:

Ответ: 124.

12. Задание 8 № 27071

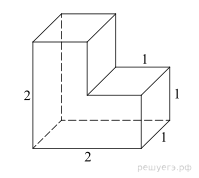Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение.

Площадь поверхности заданного многогранника складывается из четырех площадей квадратов со стороной 1, двух прямоугольников со сторонами 1 и 2 и двух граней (передней и задней), площади которых в свою очередь складываются из трех единичных квадратов каждая. Всего 4 + 4 + 6 = 14.

Ответ: 14.

13. Задание 8 № 27158

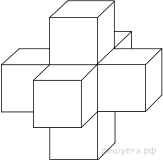Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Решение.

Поверхности креста составлена из шести поверхностей кубов, у каждого из которых отсутствует одна грань. Тем самым, поверхность креста состоит из 30 единичных квадратов, поэтому ее площадь равна 30.

Ответ: 30.

14. Задание 8 № 77155

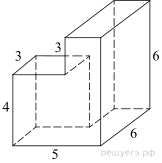Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4, уменьшенной на две площади прямоугольников со сторонами 3 и 4:

Ответ: 162.

15. Задание 8 № 77156

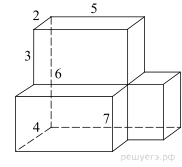Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех составляющих ее параллелепипедов с ребрами 2, 5, 6; 2, 5, 3 и 2, 2, 3, уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:

Ответ: 156.

16. Задание 8 № 77157

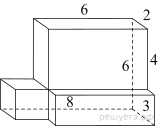Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности тела равна сумме поверхностей трех составляющих его параллелепипедов с измерениями 2, 4, 6; 1, 6, 2 и 2, 2, 2:

Ответ: 152.

17. Задание 8 № 512330

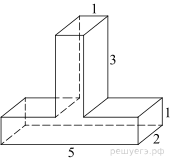Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Площадь поверхности данного многогранника складывается из площадей двух параллелепипедов со сторонами 1, 3, 2 и 1, 2, 5 за вычетом двух площадей прямоугольников со сторонами 2 и 1, которые учитываются дважды в представленном многограннике: 

Ответ: 52