Практико-ориентированные задачи в курсе математики

 

 

ПРАКТИКО-ОРИЕНТИРОВАННЫЕ ЗАДАЧИ

В КУРСЕ МАТЕМАТИКИ

 

 

 

 

 

Оглавление

1.     Введение…………………………………………………………..………..3

2.     Теоретическая часть……………………………………………..……….4

2.1   Понятие практико-ориентированной задачи………………................4

2.2   Методика решения задач с практическим содержанием…………..10

2.3   Роль и место задач с практическим содержанием в процессе        обучения математике…………………...…………………………….14

3.     Практическая часть…………………………………………………….18

4.     Список литературы……………………………………………………..29

 

 

 

 

 

 

 

 

 

 

 

1.Введение

Проблема организации практико-ориентированного обучения не является абсолютно новой, но, тем не менее, и сегодня является актуальной, так как современное образование должно ориентировать учащегося к решению тех реальных проблем, с которыми он столкнётся в жизни. Идея формирования у школьников универсальных умений, необходимых для решения жизненных и профессиональных проблем, является одной из ключевых в ФГОС.

При отсутствии мотивации процесс обучения превращается в тяжелую повинность, трудную и малопривлекательную деятельность. По мнению многих педагогов детей можно усадить за парты, добиться идеальной дисциплины, но без интереса к обучению, без внутренней мотивации учебный процесс не имеет успех. Все эти условия обусловили актуальность и явились причиной выбора темы, так как одним из средств повышения мотивации на уроках математики  является включение в систему обучения школьника практико-ориентированных задач.

         На уроках  ученики иногда задают вопрос: «А пригодится ли нам математика в дальнейшей жизни?» Это заставляет задуматься, как убедить детей, что изучать математику необходимо, чтобы правильно ориентироваться в реальной жизни. Пока еще в силу своего возраста дети не понимают, что и сегодня, и в дальнейшем они постоянно сталкиваются с теми или иными ситуациями, для решения которых необходимо пользоваться математическими знаниями и умениями. Зачастую школьникам приходится прилагать много усилий для разрешения возникших трудностей реальной жизни: они не знают с чего начать, как действовать, какое решение лучше предпринять. Для того, чтобы в реальной жизни ученики могли не бояться встретившихся на их пути проблем, необходимо в школьном курсе разбирать такие задачи, которые будут отражать реальную действительность, и которые можно с легкостью решить математическими методами, то есть практико-ориентированные задачи.

 

 

2. Теоретическая часть

2.1 Понятие практико-ориентированной задачи

        Под практико-ориентированными задачами будем понимать задачи, материал для составления которых взят из окружающей действительности и ориентирован на формирование практических навыков учащихся. В широком смысле задача рассматривается как проблемная ситуация с явно заданной целью, которую необходимо достичь. В более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать. Под практико-ориентированной задачей понимается, прежде всего, текстовая математическая задача, в которой выделяется четыре основных компонента:

1) условие – начальное состояние;                        

2) базис решения – теоретические основы решения;

3) решение – преобразование условия задачи для нахождения требуемого;

4) заключение – конечное состояние.

       Как и к любой другой задаче, задаче с практическим содержанием можно предъявить ряд требований. Во-первых, она должна обладать познавательной ценностью и оказывать воспитывающее влиянием на обучающихся. Во-вторых, ученикам должен быть понятен нематематический материал задачи. В-третьих, в задаче с практическим содержанием обязательно должны быть реальные ситуации, числовые данные, задаваемые вопросы и полученные ответы, которые ученики могли бы наблюдать в настоящей жизни. В-четвертых, задача с практическим содержанием должна отражать математическую и нематематическую проблему и их взаимосвязь. В-пятых, практическая задача не должна перекрывать её математическую значимость. В-шестых, в тексте задачи с практическим содержанием не должно быть указания на способы и средства её решения. Все выше перечисленные требования должны соблюдаться не только в задачах практического содержания, но и в других задачах.

       В литературе имеется много публикаций по рассматриваемой теме. Можно назвать таких авторов: А.С. Бикеева, Л.В. Виноградова, М.В. Егупова, О.Н. Приютко, В.И. Берник и др. В работах названных авторов дано определение прикладных задач, определение практико-ориентированных задач, определение задач с практическим содержанием, описаны требования для таких задач и мотивация обучения, функции практических задач и этапы их решения, рассматриваются причины малого количества практических задач в школьном курсе математики.

      В настоящее время современное общество нуждается в людях, которые подготовлены к настоящей жизни, занимают активную жизненную позицию, умеют работать в коллективе, имеют возможность быстро переучиться в зависимости от требований рынка и социального заказа. Несомненно, образовательные организации формируют данные качества и умения через ориентацию на практическую направленность познавательной деятельности учащихся.  Как известно, математическая подготовка школьников включает в себя теоретические знания, прикладные, практические умения и навыки. Прикладная направленность обучения математики, по мнению Ю.М. Колягина, означает ориентацию содержания и методов обучения математике на применение её в технике, смежных науках, в профессиональной деятельности и в быту. В связи с этим необходимо рассмотреть понятие прикладной задачи, которое определяется как «задача, поставленная вне математики и решаемая математическими средствами».

      По мнению исследователей, прикладная задача несёт в себе научное или практическое значение не только в математике, но и в других областях знания, поэтому к ним в рамках школьного курса относятся практические и межпредметные задачи. Такие известные методисты-математики, как Т.А. Иванова, Д. Пойа, Г.И. Саранцев, Л.М. Фридман и другие, определяли практико-ориентированные задачи как задачи, которые, по их мнению, формируют у обучающихся способность решения конкретных проблем, возникающих в реальной жизни, применяя обобщённые знания и умения по математике.

     Таким образом, практико-ориентированные задачи – это задачи из окружающей действительности, которые тесно связанны с формированием практических навыков, необходимых в повседневной жизни.

     Цель этих задач – формирование умений действовать в социально-значимой ситуации. Практико-ориентированные задачи помогают учащимся работать с информацией, выделять и отбирать главное, выстраивать собственные пути решения и обосновывать их, работать в парах и в группах, развить свои точки зрения, чувства, убеждения и желания в поисковой творческой деятельности учащихся.

      Важными отличительными особенностями практико-ориентированных задач являются :

- значимость: познавательная, профессиональная, общекультурная,

социальная, получаемого результата, что обеспечивает познавательную мотивацию учащегося;

- условие задачи сформулировано как сюжет, ситуация или проблема,

для разрешения, которой необходимо использовать знания из разных разделов основного предмета – математики, из другого предмета или из жизни, на которые нет явного указания в тексте задачи;

- информация и данные в задаче могут быть представлены в

различной форме: рисунок, таблица, схема, диаграмма, график и т.д.

- указание (явное или неявное) области применения результата,

полученного при решении задачи.

    Одной из характеристик практико-ориентированных задач является их нестандартность, т.е. в структуре задачи неопределенны некоторые из ее компонентов. Другой особенность является присутствие различной степень рациональности – это наличие нескольких способов решения задачи. Также в задаче достаточно объёмная формулировка условий при наличии избыточных или недостающих данных.

    Как показывает практика, технология обучения с применением практико-ориентированных заданий, позволяет ученика из пассивного объекта педагогического воздействия превратить в активный субъект учебно-познавательной деятельности.

     Школьники с восторгом решают и осознают задачи практического характера, им интересно наблюдать, как практическая задача превращается в теоретическую и как теоретическую задачу можно применить на практике.

      Привожу примеры практико-ориентированных задач из школьных учебников математики. Самыми распространёнными, несомненно, являются задачи на движение: движение лодки, катера по реке; движение автомобиля, пешехода по дороге; движение навстречу друг другу, в противоположные стороны либо в одном направлении. Пример такой задачи можно найти в учебнике алгебры за 8 класс: «Два велосипедиста одновременно выехали из пункта А в одном и том же направлении. Скорость первого на 2 км/ч больше скорость второго. Через 12 мин первый велосипедист остановился на 6 мин, чтобы устранить неисправность, и, возобновив движение, догнал второго велосипедиста на расстоянии 14 км от места своей остановки. Определите скорость велосипедистов».

Также не менее распространены среди практических задач задачи на производительность: изготовление деталей или изделий токарем либо бригадой, уборка урожая комбайном, вспашка поля трактором и так далее. Пример можно рассмотреть из того же учебника: «Двое рабочих выполняют некоторую работу. После 45 мин совместного труда первый рабочий был переведен на другую работу, а второй закончил оставшуюся часть работы за 2 ч 15 мин. За какое время мог бы выполнить всю работу каждый рабочий в отдельности, если известно, что второму на это понадобиться на 1 ч больше, чем первому?».

Далее среди практических задач хотелось бы отметить задачи на смеси и сплавы, которые у большинства обучающихся вызывают затруднения, потому что для получения ответа, кроме математических вычислений, требуется применение знаний на проценты. Приведем пример такой задачи: «В сплав меди и цинка, содержащий 5 кг цинка, добавили 15 кг цинка, после чего содержание цинка в сплаве повысилось на 30%. Какова первоначальная масса сплава, если известно, что в нём меди было больше, чем цинка?».

Следующим видом задач являются задачи на проценты. К ним относятся задачи о вкладах в банк, о кредитах, о прибыли либо об изменении цены на товар. Такие задачи крайне актуальны и очень полезны для обучающихся, потому что, благодаря им, ученики не только учатся работать с процентами, но и могут применить данные знания на практике самостоятельно. Пример такой задачи: «Первый банк даёт 5% годовых, а второй - 10%. Вкладчик часть своих денег положил в первый банк, а остальные - во второй. Через 2 года суммарное число вложенных денег увеличилось на 18,85%. Какую долю своих денег положил вкладчик в первый банк?».

Одним из важных видов задач с практическим содержанием, конечно, являются, так называемые, житейские задачи, в которых требуется найти, сколько понадобится краски для забора, рулонов обоев для комнаты, досок для строительства, килограммов ягод для варенья, кирпичей для камина и так далее. Такой вид задач можно встреть в учебниках по математике любого класса. Например, из алгебры за 7 класс: «Сколько рулонов обоев необходимо приобрести для того, чтобы оклеить стены квадратной комнаты, высота которой равна 3 м, площадь пола - 9 м², окна - 1,5 м², двери - 1,8 м², если одним рулоном можно оклеить 7,2 м²?».

Дополнительно из видов практических задач можно выделить экономические задачи. К ним обычно относятся задачи, требующие рассчитать расходы семьи за услуги ЖКХ, рассчитать экономическую выгоду от установления счётчика на воду, рассчитать выгоду от использования энергосберегающих приборов и так далее. К сожалению, экономических задач с практическим содержанием очень мало предлагается для решения ученикам, но данный вид формирует у обучающихся, не только математические навыки, но и подготавливает их к реальной жизни, учит экономии и бережливости. В учебнике алгебры за 7 класс предлагается следующая задача: «В квартире Ивана Петровича установлен двухтарифный счетчик, который позволяет учитывать расход электроэнергии по разным тарифам в дневное и ночное время. В январе расход электроэнергии в дневное время составил 200 киловатт (кВт), а в ночное - 20 кВт. По квитанции Иван Петрович заплатил 64 0 р. В июле расход электроэнергии в дневное время составил 20 кВт, а в ночное - 10 кВт. По квитанции Иван Петрович заплатил 380 р. Вычислите дневной и ночной тариф, расходы электроэнергии (Тариф - это цена 1 киловатта электроэнергии)».

Следующим видом задач практического содержания хотелось бы отметить исторические или старинные задачи. Рассмотрение таких задач на уроке повышает мотивацию учеников к обучению математике, расширяет их познавательную сферу. В предыдущем учебнике приводится следующая задача: «Говорят, что на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «Половина моих учеников изучает математику, четверть изучает природу, седьмая часть проводит время в молчаливом размышлении, остальную часть составляют три девы». Сколько учеников было у Пифагора?»

И в заключение можно привести примеры геометрических задач, которые непосредственно связаны с реальной жизнью и практической деятельностью учеников. В учебнике Геометрии за 10-11 классы  приводится, например,  следующая задача: «Стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает?»

 

 

 

2.2 Методика решения задач с практическим содержанием

      Способность самостоятельно решить задачу - главное умение для всех обучающихся, в том числе и для тех, кто собирается в дальнейшем изучать математику. В реальной жизни люди ежедневно ставят и решают задачи, конечно, они отличаются от задач, предлагаемых школьными учебниками математики, поэтому важным является умение решать именно задачу практического содержания, которая в наименьшей степени будет отличаться от задач повседневной жизни. Умение организовать и самостоятельно решить практическую задачу присуще активным, самостоятельным, высокоинтеллектуальным ученикам, но, к сожалению, таким умением обладает не каждый школьник.

      Чтобы научиться решать задачу с практическим содержанием, необходимо уметь анализировать условие данной задачи; уметь применять полученные ранее знания на практике, т.е. понимать, когда и какие знания нужно использовать. Также следует уметь абстрагироваться и находить общее решение, которое можно будет использовать при решении другой задачи; и, конечно, нужно контролировать и проверять каждое своё действие, т.е. проводить самоконтроль. Именно из этих действий складывается умение решать практическую задачу.

       Особенность процесса решения задач с практическим содержанием состоит в том, что необходимо более детально анализировать текст задачи, проверить задачу на избыток и недостаток условий, выявить взаимную связь с другими разделами математики и с различными сферами деятельности, правильно составить математическую модель для решения, не упустив важных условий задачи, и, наконец, необходимо верно интерпретировать полученный результат.

       Решение любой задачи, как с практическим содержанием, так и нет, можно осуществить, пройдя четыре этапа:

1) анализ условия;

2) поиск пути решения - выдвижение гипотез - составление плана решения;

3) реализация полученного плана;

4) исследование полученного решения - «взгляд назад».

      Рассмотрим каждый этапа решения задачи на конкретном примере.  В учебнике алгебры за 7 класс представлена следующая задача: «В жилом доме всего 215 квартир. Сколько из них однокомнатных, если известно, что трёхкомнатных квартир на 10 меньше, чем двухкомнатных, и на 5 больше, чем однокомнатных?». На первом этапе проводится анализ условия задачи, где должны быть осознанны все данные, необходимо четко понимать, что дано, какие условия и что нужно найти. Для этого с учениками проводится работа по составлению списка вопросов и ответов к ним. Можно составить следующий список, приведенный в таблице (табл. 1).

Таблица 1

Список вопросов и ответов к тексту задачи

Вопросы	Ответы
О чём задача?	О жилом доме, в котором есть одно-, двух- и трехкомнатные квартиры
Что требуется найти?	Количество однокомнатных квартир
Известно, сколько всего квартир?	Да, 215 квартир
Известно, сколько двухкомнатных квартир?	Нет
Известно, сколько трехкомнатных квартир?	Нет
Что известно про трехкомнатные квартиры?	Их на 10 меньше, чем двухкомнатных, и на 5 больше, чем однокомнатных

 

    По возможности все данные сводятся в единую схему, таблицу, чертеж, рисунок или краткую запить. К данной задаче можно составить таблицу  следующим образом (табл. 2):

Таблица 2

Таблица по тексту задачи

Квартира	Однокомнатная	Двухкомнатная	Трехкомнатная
Количество	?	?	?, на 10 меньше, чем однокомнатных
Всего 215 квартир

 

     Для выявления того, как обучающийся понял тест задачи, можно попросить его пересказать задачу своими словами, также необходимо обязательно со всеми учениками проработать постановку вопросов и ответов к ним.

     Второй этап выполняется через введения взаимных связей между тем, что дано, и тем, что надо найти. Если напрямую этого сделать не получается, то следует переформулировать данные задачи и заново попытаться связать условия и требования. Поиск пути решения может осуществляться как от условия к заключению, так и наоборот, либо двигаться сразу с двух сторон. Применительно к данной задаче ученики, скорее всего, предложат её решить через введение новой переменной. Данный способ распространен и несложен. Для упрощения, лучше всего за x обозначить количество однокомнатных квартир, чтобы сразу получить нужный ответ. Тогда представленная таблица по тексту задачи (табл. 2) будет выглядеть следующим образом (табл. 3):

Таблица 3

Таблица по тексту задачи после введения переменной

Квартира	Однокомнатная	Двухкомнатная	Трехкомнатная
Количество	x	x+5+10	x+5
Всего 215 квартир

       Далее необходимо сложить количество однокомнатных, двухкомнатных и трёхкомнатных квартир, полученное введением переменной x, и приравнять к общему количеству квартир в доме, т.е. к 215. Поиск пути решения завершен.

     На третьем этапе важно грамотно и достаточно развернуто записать решение, каждое действие должно быть обосновано и доказано, иначе задача не будет считаться решённой. Это важно проделывать при решении любой задачи, особенно на начальных этапах усвоения определённого метода. Применительно к данной задаче решение оформляется с помощью уравнения: x + (x+5+10) + (x+5) = 215. После раскрытия скобок и приведения подобных слагаемых уравнение примет вид: 3x = 195. Отсюда, x = 65. Ответ: 65 однокомнатных квартир в жилом доме.

      На четвертом этапе проверку полученного ответа можно осуществить, подставив его в краткую запись (в данном примере в таблицу 3). Можно допустить, что полученный ответ равен не 65, а, например, 30. Подставив его в таблицу 3, можно заметить, что однокомнатных квартир 30, двухкомнатных - 45, трехкомнатных - 35, а всего 30 + 45 + 35 = 110. Дети заметят, что задача решена неверно, а, подставив полученный ранее ответ, всё получается правильно. Кроме того, на данном этапе можно предложить ученикам решить туже задачу, только за x взять количество не однокомнатных квартир, а двухкомнатных или трехкомнатных, и сравнить получившиеся результаты.

    К сожалению, не многие учителя проводят четвертый этап работы с практической задачей, потому что это трудоемко и требует много времени. Но исследование полученного решения проводить надо, потому что именно на этом этапе можно убедиться в осознании учениками решения данной задачи.

     Итак, способность самостоятельно решить практическую задачу - главное умение для всех обучающихся. Данное умение очень важно, потому что, зная методы решения задач практического содержания, обучающиеся учатся взаимодействовать с разными задачами, которые могут встретиться им в повседневной жизни. При решении задач с практическим содержанием ученики осваивают алгоритм решения таких задач, у них развиваются ценные навыки применения математических знаний, приходит осознание роли математики в целом. Кроме того, считаю, что благодаря практическим задачам у школьников воспитывается трудолюбие, самостоятельность, настойчивость, активность, формируется когнитивный интерес, они помогают выработать и отстоять свою точку зрения.

2.3  Роль и место задач с практическим содержанием в процессе обучения математике

         Чтобы определить роль и место задач с практическим содержанием в процессе обучения математике следует рассмотреть, какие функции они выполняют. Л.В. Виноградова выделяет воспитывающие, развивающие и обучающие функции. Воспитывающая функция таких задач заключается в том, что в ней может содержаться различная информация из разных областей знания. С помощью данных задач расширяется кругозор знаний,  и увеличиваются познавательные возможности. Развивающая функция состоит в том, что практические задачи вырабатывают способность применения теоретических, математических знаний на практике, учат выделять общие методы решения и применять их на новых задачах, развивают внимание, память, логическое мышление, воображение учеников. Обучающая функция проявляется на каждом этапе изучения нового материала: на этапе подготовки к изучению, на этапе усвоения, на этапе первичного применения полученных знаний и на этапе контроля и закрепления.

На сегодняшний день интерес к задачам с практическим содержанием только увеличивается, потому что их включают в содержание как ОГЭ, так и ЕГЭ. Разбор задач практического содержания с учениками помогает повысить практическую значимость изучения математики в школе; научить необходимым навыкам решения таких задач и умениям рассчитывать величины и их примерное значение; усилить интерес, мотивацию к обучению математике; увеличить результативность обучения школьного курса математики.

 Хотя  задачи с практическим содержанием с каждым годом становятся все актуальнее, в школьном курсе математики крайне мало отводится времени  на такие задачи.  На основе  анализа содержания школьных учебников, мною была составлена  следующая таблица (табл.4), отражающая процентное соотношение практико-ориентированных задач в школьных учебниках.

 

Таблица 4

Процентное соотношение практических задач в школьных учебниках

 

Название учебника	Процентное соотношение практических задач
Математика, 5 класс	≈32%
Математика, 6 класс	≈ 23%
Алгебра, 7 класс	≈ 9%
Алгебра, 8 класс	≈ 5%
Алгебра, 9 класс	≈ 11%
Алгебра и начала математического анализа, 10 - 11 класс	≈ 4%
Геометрия, 7 - 9 класс	≈ 3%
Геометрия, 10 - 11 класс	≈ 2%

 

     Таким образом, возникает необходимость создания некой копилки или сборника  практико-ориентированных задач, в которую войдут не только задачи из учебников или сети Интернет, но и составленные учащимися из опыта своей жизни.

     В реальной жизни существует мало ситуаций, в которых применяется одно решение либо один ответ. Чаще же в повседневных проблемах людям приходится делать выбор, потому что и решение может быть не одно, и ответов несколько. При решении практических задач нужно учить детей размышлять, искать разные ответы, самим просчитывать варианты развития задачи и выбирать самый разумный. Такой вид заданий заставляет детей думать критически, осмысленно и внимательно рассматривать проблему, которая затрагивается в практической задаче.

     Из чего можно заключить, что роль практических задач огромна. Они раскрывают всё многообразие практического применения математических знаний, полученных на уроках; закрепляют и углубляют данные знания на практике; наглядно иллюстрируют учебный материал; развивают логическое, познавательное мышление; учат детей самостоятельно принимать решение и видеть значимость изучения математики в целом. Практические задачи должны занимать главное место в процессе обучения математики. Необходимо постоянно тренироваться в умении использовать полученные математические знания в реальной жизни, на каждом уроке либо через урок предлагать ученикам решить задачу с практическим содержанием. Тем самым у обучающихся повысится активная деятельность, улучшатся мыслительные операции, произойдет прочное усвоение математических знаний, будут формироваться математические навыки.

     Можно рассмотреть некоторые способы мотивации учеников с помощью практических задач:

1)                если изначально рассмотреть какие-либо физические явления или технические проблемы и на основе этого сформулировать для решения практическую задачу, то обучающиеся воспримут её намного лучше и будут решать её с большим желанием, потому что они наглядно рассмотрели, из чего и как именно она возникла.

2)                для мотивации обучения математике можно использовать исторические или старинные задачи, которые создадут эмоциональный настрой в классе, вызовут интерес к новой теме, несмотря на то, что изначально она им может показаться совершенно неинтересной. Для большей стимуляции детей к обучению можно использовать задачи с необычной формулировкой, ссылаясь на древний источник.

3)                перед изучением новой темы можно предложить практическую задачу, которая изначально покажется ученикам простой, и ответ на которую они дадут незамедлительно. Но полученные ответы окажутся разными, из-за чего возникнет спор. Активные дискуссии во время спора увлекут учащихся, им захочется узнать верное решение и ответ, который они смогут получить, только изучив новую тему.

4)                в начале урока учитель может предложить ученикам практическую задачу, ответом на которую будет некруглое число. Школьники подумают, что допустили где-то ошибку и получили неверный ответ, проверив все вычисления, дети придут в недоумение, которое учитель должен развить, изучив новую тему урока.

5)                 для мотивации обучения можно использовать практические задачи из банка заданий по ОГЭ или ЕГЭ, мотивировав учеников тем, что полученные навыки и умения пригодятся им для сдачи экзамена.

6)                 для мотивации можно использовать практические задачи, которые будут проиллюстрированы с помощью компьютерной техники, способствующей творческому умению решать задачи, устойчивой мотивации получения нового знания.

    В дополнение, задачи с практическим содержанием можно использовать на уроке для того, чтобы показать дальнейшую перспективу применения полученных знаний в повседневной жизни.

 

 

 

 

 

 

 

 

 

3. Практическая часть

На уроках математики и во внеурочной деятельности я довольно широко использую практико-ориентированные задачи, которые были составлены к каждой конкретной теме отдельно.

Привожу  для примера несколько составленных практико-ориентированных задач.

Математика ,5-6  классы.

Тема: «Числовые и буквенные выражения»

Учащимся предлагается решить следующие задачи на закрепление:

1. Цена молока стоит – (?) р. за упаковку, а цена творога – на 45 р.

 

больше. Запишите на математическом языке:

a) цену 1 упаковки молока;

b) стоимость трёх пачек творога;

c) стоимость 5 пачек молока;

d) стоимость молочной продукции из 2 упаковок молока и 2 пачек творога вместе.

2. Цена 1 кг конфет стоит – (?) р., а шоколад в 3 раза дешевле.

 

Запишите на математическом языке:

a) цену 1 кг конфет и шоколадки;

b) стоимость пяти шоколадок;

c) стоимость трёх кг конфет;

d) разницу между 2 кг конфет и 3 шоколадок.

 

Тема: «Умножение и деление обыкновенной дроби на натуральное число»

Задача:Какое расстояние вы преодолеваете, идя из дома в школу за 1 мин? За 5 мин? За 10 мин?

Тема: «Масштаб»

Данная задача предназначена для домашней работы:

«Начертите схему своего маршрута, по которому вы ходите из своего дома в школу. Найдите длины этих маршрутов и соответствующие расстояния. Схему выполните в масштабе 1:1000»

Тема: «Круговые диаграммы»

Задача: Изобразите на круговой диаграмме расходы семейного бюджета за месяц в процентах.

Тема «Прямоугольный параллелепипед»

Данная задача предназначена для домашней работы.

«Вычислить площадь и объём своей комнаты и всей квартиры (дома), записав все размеры в таблицу. Изготовить модель своей комнаты в виде  прямоугольного параллелепипеда, с размерами, уменьшенными в 100 раз»

          Кроме этого учащимся можно предложить выполнить следующие проекты:

Проект «Покупка в кредит». Необходимо исследовать возможность совершить покупку, на приобретение которой пока нет денежных средств. Что выгоднее – заработать и накопить, сохраняя деньги в «банке», заработать и накопить, открыв счет в сбербанке; совершить покупку в кредит, выплачивать который нужно будет из заработанных средств? Какие виды кредитов более выгодны? Соответствие цены и качества. Проведение необходимых расчетов по погашению кредита. Финансовые издержки (сколько денежных средств затрачено дополнительно на оплату кредита, что кажется учащемуся более выгодным и правильным – покупка в кредит, или накопление денежных средств на счете в банке, а затем совершение покупки).

Учащиеся получают так же необходимые дополнительные разъяснения об основах трудового законодательства для несовершеннолетних и возрасте, начиная с которого они могут получить кредит.

Проект «Идеальный ремонт» может быть разработан учащимися как творческое задание при изучении темы «Площадь и периметр». Проект может включать разделы: фотографии жилых помещений; планы жилых помещений; каталоги отделочных материалов; прайсы с указанием цен на различные отделочные материалы; прейскурант стоимости услуг ремонтной фирмы; расчеты площадей отделываемых поверхностей; расчеты необходимого количества отделочных материалов; расчеты стоимости отделочных материалов; расчеты стоимости услуг ремонтной фирмы; расчеты общей стоимости ремонта. Класс может быть разделен на несколько групп – строительные бригад: оклейка обоями и окрашивание стен и потолков;  укладка паркетных полов; отделка ванных комнат кафелем и др.

Проект «Здоровое питание».  Разрабатывается при изучении темы «Проценты». Учащиеся изучают зависимость между энергозатратностью организма и энергоёмкостью (калорийностью) пищи для организации здорового питания школьника. В результате выполнения проекта учащиеся учатся вычислять свою дневную норму, считать калорийность своего суточного рациона питания.

Решение практико - ориентированных задач также использую в работе по профориентации. В начале учебного года учащиеся пишут  домашнее мини-сочинение : «Математика в жизни и профессии моих родителей». Затем учащиеся по группам обобщают результаты , подбирают задачи из учебника, имеющие отношение к профессии родителей. Завершаем этот этап работы конструированием собственных задач. По итогам работы группы оформляю мини проекты или презентации: "Математика - в профессии моих родителей".
                 Примеры задач

	Профессия	Задачи
1.	Кулинар	1.     Мама решила приготовить салат  из огурцов, помидоров и редиски. Вся масса салата должна составить 400 г. Сколько нужно положить помидор, если масса огурцов составляет 150 г., а масса редиски в 2 раза меньше массы огурцов? 2.      Хозяйка собрала 17 кг яблок. Сколько получится свежевыжатого сока, если сок составляет 80% от массы всех яблок? 3.     Купили 15 кг груш. На компот решили истратить 40% все груш, а остальное пошло на варенье. Сколько кг сахара нужно купить для варенья, если на 1 кг свежих груш нужно 800 г. сахара? 4.     Для приготовления летнего салата для семьи нужно 500г помидор по цене 25 руб. за 1 кг, 300 г огурцов по цене 40 руб. , 30 г зеленого лука по цене 6 руб., 50 г сметаны по цене 50 руб. за баночку массой  200 г. Какова  будет стоимость салата?
2	Продавец	1.     В магазин привезли 400 кг апельсинов. В первый день продали 15%, а во второй день 0,5 оставшихся. Сколько осталось апельсинов в магазине? 2.     В школьный буфет привезли пирожки. Ученики старших  классов скупили 120 пирожков, что составило 48%  всего количества. Сколько всего привезли пирожков? Сколько пирожков купили ученики младших классов,  если 17 пирожков остались не проданными?
3	Строитель	1.     Для строительства гаража  можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо    5 м3 пеноблоков и 2 мешка цемента. Для бетонного фундамента необходимы 4 т щебня и 40 мешков цемента.  1 м3  пеноблоков  стоит 2400 руб., щебень стоит 640 руб. за 1 тонну, а мешок цемента стоит 240 руб. Сколько будет стоить материал если выбрать наиболее дешевый вариант? 2.     Постройка дома начинается с котлована. Требуется выкопать котлован размером 10х 11 м  и глубиной 2 метра. Сколько нужно вывезти машин грунта, если грузоподъемность одной машины 10 м3?
4	Медсестра	1.     В больницу поступила девочка с отравлением. Сколько таблеток активированного угля ей необходимо дать в течение дня, если известно, что на 1 кг массы тела требуется 0,25 мг лекарства, а ее вес составляет 50 кг? 2.     Больному прописано лекарство, которое нужно пить о 0,5 г. 3 раза в день в течении 8 дней. В одной упаковке 8 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5	Бухгалтер	1.     Клиент взял в банке кредит  18000 руб. на год под 12% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно? 2.     Какой будет заработная плата после повышения ее на 30%, если до повышения она составляла 8760 руб., и с работника берется подоходный налог 13%?
6	Водитель	1.     Водителю выдали американский автомобиль, на спидометре которого скорость измеряется в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 26 мили/час?  Ответ округлить до целого числа. Американская миля равна 1609 м. 2.     Таксист за месяц проехал 10000 км. Стоимость 1 л бензина 32 руб. Средний расход бензина на 100 км составляет 7 литров. Сколько рублей потратил таксист на заправку автомобиля?
7	Воспитатель	В летнем лагере 245 детей и 29 воспитателей. В автобус помещается не более 46 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?
8	Зав. производством в кафе (столовой, ресторане)	В школьной столовой питается 145 человек. На каждого полагается 15 г. масла в день. Сколько упаковок масла по 250 г. понадобится на 1 день?
10	Дорожник	Для приготовления асфальта берется 43,06% щебня,     40,19 % песка дробленого,4,78% песка природного,   4,31 %битума, 7,66 % минерального порошка. Сколько надо взять каждого вещества, чтобы сварить 15 т асфальта?

 

          В своей работе я также часто использую технологию квестов.

           Квест- это  одна из форм интерактивной игры в образовательном процессе . «Квест »- в переводе с английского языка означает «целенаправленный поиск». История появления квестов связана с одним из жанров компьютерных игр, представляющих управление главным героем, которые выполняет проблемное задание в виде головоломок, задач, требующих умственных усилий. При этом игра может включать старинные математические, занимательные, геометрические, практические задачи, которые необходимо решить. Условия игры могут быть различными: могут соревноваться как команды, так и отдельные ученики. Сам термин «квест» как образовательная технология был применен профессором университета Сан-Диего Берни Доджем в значении поисковой системы, которая призвана находить решение поставленной главной задачи прохождением промежуточных станций, где необходимо выполнить задание, чтобы добыть ключ, или перейти на следующую станцию. Возможно есть некоторая схожесть со всем известными играми «по станциям».

          Выделим основные виды квестов:

• по месту проведения: веб-квесты, квесты в формате урока, квесты во внеурочной деятельности;

 • по форме организации: линейные, штурмовые, кольцевые. Линейные квесты предполагают процесс решения задач одну за другой – последовательно, так что один этап открывает возможность переходить к следующему этапу. Штурмовой квест включает наличие определенного перечня подсказок, позволяющий сделать выбор. Наконец, кольцевые квесты предполагают участие команд или отдельных участников из разных точек маршрута, и завершение - в решении конечной проблемы. Структура построения квеста может быть представлены в виде схемы, представленной на рисунке 1.

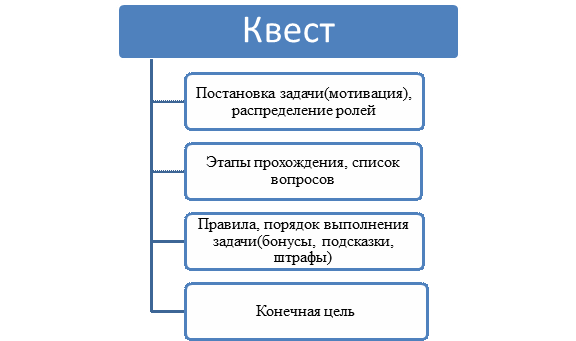
                                                          Рис.1 Структура  квеста

 

        Организацию реализации математического квеста как игровой технологии на уроке можно представить в виде следующих этапов:

 • дидактические цели ставятся перед учащимися в виде игровой задачи, решение которой позволяет открыть «ключ», «шифр», найти клад, возможность перейти к следующему заданию;

• учебная деятельность подчинена правилам квеста: это может быть «зарабатывание» условных денег, баллов, фишек. Вводится соревновательная деятельность, способствующая переходу дидактических задач к игровым;

• учебный материал является средством, а его успешное усвоение связывается с игровым результатом.

Математический квест «Мой веселый день»

      Цели занятия:

·        обучение переносу теоретических знаний по математике в практическую жизнедятельность учащихся

·        применение знаний и умений в познавательной и предметно-практической деятельности.

·        подготовка учащихся к реальной жизни

·        формирование способности решать личностно-значимые проблемы

·        формирование ключевых компетенций: ценностно-смысловой, общекультурной, учебно-познавательной, информационной, коммуникативной, социально-трудовой и компетенции личностного самосовершенствования

·        формирование метапредметных  и  универсальных учебных действий с учетом реальных потребностей и интересов в общении и познании.   

·        ориентация на тесную связь обучения с непосредственными жизненными потребностями, интересами и социокультурным опытом учащихся. 

·        получение учащимися знаний, которые могут быть применимы не только в рамках образовательного процесса, но и в реальных жизненных ситуациях.

образовательные:

·         расширение и закрепление знаний обучающихся по математике ;

·         совершенствование умений применять полученные знания на практике;

·         внедрение интерактивных игровых технологий в образовательный процесс;

развивающие:

·         повышение интереса к изучению математики;

·         развитие умений поиска необходимой информации, способности грамотно формулировать свои мысли, идеи;

·         развитие логического мышления, умения быстро принимать решения и аргументировать свой выбор;

·         развитие навыков работы в команде;

·         развитие коммуникативной компетенции обучающихся;

воспитательные:

·         формирование интереса к решению нестандартных задач и умения применять полученные знания на практике;

·         воспитание активной, инициативной личности,

·         формирование чувства ответственности за членов своей команды.

       Образовательные технологии: информационно-коммуникационные, игровые технологии, педагогика сотрудничества.

     Участники мероприятия: ученики 5-9 классов

Игра начинается с разбиения на команды по 3-6 человек в зависимости от общего количества учащихся. Каждая команда представляет из себя семью (мама, папа, дети), распределяются роли. Команда получает распорядок дня со списком заданий (мероприятий)-5-6 пунктов, обязательных для выполнения, также дополнительные мероприятия-бонусы.

 Примеры заданий (мероприятий) в  распорядке дня:

1)    Покупки в магазине

2)    Аптека

3)    Приготовление обеда

4)    Посещение цирка (кино, театра)

5)    Транспорт

6)    Оплата коммунальных услуг

7)    Подарки и т.д.

Каждое задание содержит 3 задачи различных уровней сложности. Правильное решение задачи оценивается смайлами. Команды вправе сами выбирать задание, но могут выполнить и все 3 задачи. Возвращаться обратно к пройденным пунктам распорядка нельзя.

        Примеры некоторых заданий:

Покупки в магазине: 1. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?(1 смайл)

2. Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?(2 смайла)

3.(практическое) Для по­крас­ки 1 м² по­тол­ка тре­бу­ет­ся 240 г краски. Крас­ка про­да­ет­ся в бан­ках по 2,5 кг. Сколь­ко банок крас­ки нужно ку­пить для по­крас­ки по­тол­ка в этом классе? Оборудование: метровая линейка. (3 смайла). Данную задачу можно чуть усложнить, если вместо расхода краски на квадратный метр площади предоставить учащимся этикетку с банки с краской для нахождения недостающих данных.

Аптека: 1. Больному про­пи­са­но лекарство, ко­то­рое нужно пить по 0,5 г 3  раза в день в те­че­ние 21 дня. В одной упа­ков­ке 10 таб­ле­ток лекарства по 0,5 г. Ка­ко­го наименьшего ко­ли­че­ства упаковок хва­тит на весь курс лечения?(2 смайла)

2. В больницу поступила девочка с отравлением. Сколько таблеток активированного угля ей необходимо дать в течение дня, если известно, что на 1 кг массы тела требуется 0,25 мг лекарства, а ее вес составляет 50 кг?(2 смайла)

3.(практическое)  У ребенка хроническое заболевание. Рассчитать количество таблеток, необходимых для проведения одного  курса лечения. Оборудование: инструкция к лекарству, весы напольные. (3 смайла)

          После выполнения всех пунктов распорядка дня команда, которая справилась быстрее, имеет право выполнить дополнительные задания, дающие возможность заработать дополнительные баллы.

        Примеры дополнительных заданий:

1.     Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

2.     Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.

Пользователь предполагает, что его трафик составит 600 Мб в месяц и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Мб?

3.                 Строительный подрядчик планирует купить 5 тонн облицовочного кирпича у одного из трех поставщиков. Вес одного кирпича 5 кг. Цены и условия доставки приведены в таблице. Во сколько рублей обойдется наиболее дешевый вариант покупки? 

 

Заключительным этапом квеста является аукцион, где команды на заработанные смайлы покупают себе призы.

 

 

 

 

 

 

 

 

 

 

 

 

 

Список литературы

1.                 Атанасян Л.С. Геометрия. 10–11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.], – 22-е издание – М.: Просвещение, 2013. – 255 с.

2.                 Бикеева А.С. Какие задачи хотелось бы решать в школе // Математика в школе. 2013. №1. С. 3-7.

3. . Виноградова Л.В. Методика преподавания математики в средней школе: учебное пособие / Л.В. Виноградова. — Ростов н/Д.: Феникс, 2005. – 252 с.

4. Егупова М.В. Использование практических задач в обучении геометрии // Математика в школе. 2011. №10. С. 39 — 44.

5. Литвинова И.Н. Математический квест как современная форма игровой технологии, 2017// [https://cyberleninka.ru/article/v/matematicheskiy-kvest-kak-sovremennaya-forma-igrovoy-tehnologii]

6.Печёнкина Е.Н. Практико-ориентированные задачи на уроках математики в основной школе // Электронный ресурс [http://rudocs.exdat.com/docs/index-100680.html]

7. Приютко О.Н., Берник В.И. Практико-ориентированные задачи в контексте изменения программ школьного курса математики [Электронный ресурс] // Практико-ориентированные задачи в контексте изменения программ школьного курса математики. URL http://Matem/praktiko-orientzadachi/izmen/progr/matematika

8.  Соболев С.К. Роль и место прикладных задач в обучении математики. [Электронный ресурс] // Роль и место прикладных задач в обучении математики. URL https://kopilkaurokov.ru/matematika/prochee

9. Ябурова Е.А. Задачи с практическим содержанием как средство реализации практико-ориентированного обучения математике - http://www.dissercat.com/content/zadachi-s-prakticheskim-soderzhaniem-kak-sredstvo-realizatsii-praktiko-orientirovannogo-obuc