Практико-ориентированные задачи в курсе математики (задачи на проценты)

Практико-ориентированные задачи в курсе математики

(задачи на проценты)

Преподаватель  математики

 Усова Е.В.

Содержание

Введение……………………………………………..…………………………….2

Понятие о проценте……………………………………………………………….4

Основные типы задач на проценты………………………………………….......9

Примеры практико-ориентированных задач………………………………..…11

Простейшие задачи………………………………………………………….......11

Задачи на проценты, решаемые путем составления уравнения или системы уравнений………………………………………………………………………...13

Задачи на концентрацию………………………………………………………...15

Сложные проценты……………………………………………………………...19

Заключение……………………………………………………………………….21

Список источников и литературы………………………………………………22

Введение

Проценты - одна из самых непростых тем школьной математики. Она трудно усваивается учащимися.  И вместе с тем проценты очень важный материал, потому что знание процентов важно в практическом плане. В этой  работе сделана попытка проследить изучение процентов в курсе основной школы на примере практико-ориентированных задач.

К моменту изучения процентов в 6 классе у учащихся сформировано понятие о проценте как о сотой доле величины, им известен знак «%» и сформирован первичный опыт решения простейших задач на проценты, поэтому следующим шагом может являться уточнение понятия процента. В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями. Учащиеся учатся выражать проценты числом и число процентами как для общего случая, так и для основных дробей: половина – 50%, четверть – 25%, три четверти – 75%, пятая часть – 20% и т.д., переводить на язык процентов речевые обороты, выражающие изменение величин (например, «увеличить в два раза», «уменьшить на четверть») и делать обратный перевод.

«Понять – значит привыкнуть и научиться применять» (Ричард Флейнман, лауреат Нобелевской премии по физике "за фундаментальные работы по квантовой электродинамике, имевшие глубокие последствия для физики элементарных частиц"). Именно привыкания к пользованию часто не хватает нашему школьнику для понимания изучаемого материала. Мы торопим его: успевай запоминать, успевай усвоить. Поможем детям привыкнуть и спокойно пользоваться полученными знаниями.

Для человека чрезвычайно важно не столько энциклопедическая грамотность, сколько способность применять обобщённые знания и умения для разрешения конкретных ситуаций и проблем, возникающих в реальной действительности. По мнению известных психологов и методистов – математиков, формировать способность разрешения проблем помогают специальным образом подобранные задачи. Это практико-ориентированные задачи.

Практико-ориентированные задачи – это вид сюжетных задач, требующий в своем решении применения всех этапов метода математического моделирования. Под задачей с практическим содержанием понимается математическая задача, фабула которой раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит ее с использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций.

Понятие о проценте

Процентом от любой величины называется одна сотая ее часть.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например, 65%=  Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, его нужно умножить на 100, например 0,65=65%.

Правило перевода процентов в числа и чисел в проценты: p%=p:100=

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раза» говорится об одном и том же. Точно так же увеличить в 2 раза – это значит увеличить на 100%, увеличить в 3 раза – это значит увеличить на 200%, уменьшить в 2 раза – это значит уменьшить на 50%. Для   наглядного представления удобно использовать графическую модель, которая помогает учащимся лучше осознать смысл процентов (рис.1).

Рис. 1

Понимание разных форм выражения одного и того же изменения величины с помощью процентов и без них является сегодня важным жизненным навыком.

Примеры упражнений, направленных на актуализацию понятия процента как одной сотой части величины.

Пример 1. Верно ли, что:

а) 1 см составляет 1% от 1 м;

б) 1 г составляет 1% от 1 кг;

в) 245 человек составляют больше 1% от 10 тыс. человек?

При выполнении следующих упражнений учитель предлагает использовать графические модели для наглядного представления смысла процентов. Полученный опыт работы с моделями будет применяться при выполнении других заданий на проценты.

Пример 2. Объясни смысл предложений и построй их графическую модель:

а) в воздухе содержится 21% кислорода;

б) цена на компьютеры снизилась на 10%;

в) бригада выполнила план на 150%;

г) бригада перевыполнила план на 150%.

3. Построй графическую модель высказываний, изобразив в обоих случаях продажную цену товара отрезком в 20 клеток.

а) «Доход составляет 25% продажной цены товара»;

б) «Доход составляет 25% себестоимости товара».

В каком случае доход составляет большую величину?

Решение.

а) 25% от 20 клеток (100%) – 5 клеток; б) 25% от 20 клеток (125%) – 4 клетки.

Закрепить умение выражать проценты числами и числа процентами можно на следующих упражнениях.

1.Замени проценты числами: 2%, 56%,  .

2.Вырази в процентах части величин: 0,04; 0,32; 1,7;  .

Сформировать представление о приблизительном значении третьей части величины в процентном выражении как 33,3% учащиеся могут при решении следующих задач.

1.Один ученик сказал: «Одна треть всех учащихся школы – это 30% всех учащихся школы». Прав ли он?

2.На совете акционеров говорилось: «Две трети планируемых инвестиций направлены в производство, значит, на социальную сферу остается 30%». Согласен ли ты с этим утверждением?

Следует обратить внимание на задания, которые показывают «хитрость» процентов: одна  и та же величина составляет различное количество процентов при сравнении ее с различными данными, одно и то же количество процентов от разных величин дает различные значения.

Задача 1. В классе мальчиков на 25% больше, чем девочек. На сколько процентов девочек в этом классе меньше, чем мальчиков?

Задача 2. В первом квартале доля продажи товаров отечественных производителей увеличилась с 20% до 25%, а во втором – с 25% до 30%. В каком квартале процент увеличения был больше? (Процент увеличения – это отношение прироста в процентах к первоначальной доле в процентах.)

В первой задаче разность между количеством мальчиков и девочек составляет 25% при сравнении числа мальчиков с числом девочек (за 100% берется количество девочек), но только 20% при сравнении числа девочек с числом мальчиков (за 100% берется количество мальчиков). Это задание лучше выполнять с использованием графической модели (рис.2).

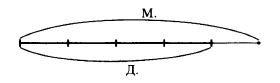
Рис.2

Во второй задаче процент увеличения за первый квартал составляет 5% от 20%, т.е. одну четверть, или 25%, а за второй квартал те же 5 % берутся от 25% и составляют уже одну пятую, или 20%. Следует обратить внимание учащихся на это особенность процентов: казалось бы, и в том и в другом квартале доля продаж увеличилась на одинаковое количество процентов, но в первом квартале процент увеличения был значительнее.

Основные типы задач на проценты

Основная содержательная цель уроков по данной теме: систематизировать задачи на проценты,   вывести формулу процентов, сформировать умение использовать эту формулу для решения задач на проценты. Проценты можно выразить дробями, поэтому задачи на проценты решаются как задачи на дроби. Перед изучением этого вопроса учителю целесообразно провести подготовительную работу, в ходе которой актуализируется умение решать основные задачи на дроби: нахождение дроби от числа, числа по значению дроби и отношения чисел. После этого можно приступить к рассмотрению основных типов задач на проценты, при этом использование графической иллюстрации дает большую наглядность.

Пусть a – некоторая величина, взятая за 100%, b –  ее часть, которая составляет p% от a. В зависимости от того, что надо найти, a, b или p, можно выделить три основные задачи на проценты (рис.3).

 Рис.3

1. Нахождение процента от числа. Чтобы найти p% от числа a, надо это число умножить на дробь :                .

2. Нахождение числа по его проценту.   Чтобы найти число по его части, составляющей   p% этого числа, надо эту часть разделить на дробь:   .

3. Нахождение процентного отношения двух чисел. Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100:  .

В результате рассмотрения этих задач знания учащихся о задачах на проценты систематизируются, устанавливается взаимосвязь между ними: формулы, описывающие решение задач всех трех типов являются преобразованиями одной и той же формулы – формулы процентов               .

Знание этой формулы дает новый подход к решению задач на проценты.

Этот способ позволяет рассматривать задачи на проценты как задачи на формулу произведения и дает новый подход к их решению, сводящийся к подстановке в формулу известных данных и выполнению формальных преобразований. Тем самым учащимся не приходится расширять круг известных типов задач, задачи на проценты решаются ими уже известным способом, что особенно ценно для менее подготовленных учащихся.

Примеры практико-ориентированных задач

Простейшие задачи

При обучении решению основных типов задач на проценты учитель предлагает задачи с практическим содержанием.

Задачи на нахождение процента от числа:

1.Сколько составляют:

а) 8% от 6 кг; б) 30% от 15 м; в) 75% от 80%.

2. Что больше:

а) 15% от 17 или 17% от 15?

б) 1,2% от 48 или 12 % от 480?

в) За поиск покупателей фирма предлагает своему агенту-дилеру вознаграждение в размере 6% от суммы заказа. На какое вознаграждение может рассчитывать дилер, если он нашел подходящий заказ на сумму 20000 рублей?

г) Сколько соли получится при выпаривании 375 граммов 12% раствора соли?

д) Сколько будет, если 100 р. увеличить на 300%?

е) Подоходный налог установлен в размере 13% от начисленной зарплаты. Какую зарплату получит работник, если ему начислено 25000 рублей?

ж) В референдуме приняли участие 60% всех жителей города, имеющих право голоса. Сколько человек приняли участие в референдуме, если в городе 150 тыс. жителей, а право голоса имеют 83%?

Задачи на нахождение числа по его проценту:

1. Найти, от какой величины:

а) 7% составляют 7 р.;

б) 25% составляют 10г;

в) 12% составляют 36 экземпляров.

2. Фирма платит рекламным агентам 5% от стоимости полученного заказа. На какую сумму агенту надо найти заказ, чтобы заработать 2000 рублей?

3. Сколько было, если после увеличения на 30% стало 520 р.?

4. В каком случае первоначальная цена была больше:

а) если при скидке 5% заплачено 190 р.;

б) если при скидке 10% заплачено 180 р.?

Задачи на нахождение процентного отношения чисел:

1. Длину прямоугольника увеличили на 20%, а ширину – на 25%. На сколько процентов увеличилась площадь прямоугольника?

2. Имеются два раствора соли массой 80г и 120г. В первом растворе содержится 12 г соли, а во втором – 15г соли. Чему равна концентрация этих растворов?

3. При выполнении работы по математике15% учеников класса вовсе не справились с задачей, 255 учеников допустили ошибки, а остальные 24 человека решили ее верно. Сколько учеников класса выполняли работу?

Решение подобных задач повышает практическую значимость математики в глазах учащихся. После отработки трех основных типов задач на проценты учащиеся решают составные задачи на проценты.

Задачи на проценты, решаемые путем составления уравнения или системы уравнений

По мере изучения уравнений и систем уравнений (7 класс) учащиеся получают возможность решать более сложные задачи на проценты. Вот примеры задач, которые можно предложить ученику 7 класса.

1. Семь одинаковых рубашек дешевле куртки на 2%. На сколько процентов десять таких же рубашек дороже куртки?

Решение:

Пусть цена куртки x р.– 100%, тогда стоимость 7 рубашек составляет 98% от цены куртки, т.е. 0,98x. Значит, цена рубашки равна 0,98x:7=0,14x, а 10 рубашек стоят 1,4x. Посчитаем, на сколько процентов десять таких же рубашек дороже куртки: 1,4x – x=0,4x, что составляет 40% от цены куртки. Ответ: 40%.

2. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась втрое, общий доход семьи вырос бы на 112%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 3%. Сколько процентов от общего дохода семьи составляет зарплата жены?

Решение. Пусть зарплата мужа – это %, зарплата жены - %, а стипендия дочери - % от общего дохода семьи. Запишем условие задачи в виде таблицы.

Составим и решим систему уравнений.

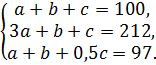
Решая систему, получаем, что

Ответ: 38%.

3. Митя, Артём, Паша и Женя учредили компанию с уставным капиталом 200000 рублей. Митя внёс 18% уставного капитала, Артём  — 60000 рублей, Паша  — 0,18 уставного капитала, а оставшуюся часть капитала внёс Женя. Учредители договорились делить ежегодную прибыль пропорционально внесённому в уставной капитал вкладу. Какая сумма от прибыли 1100000 рублей причитается Жене? Ответ дайте в рублях.

Решение. Посчитаем, сколько процентов уставного капитала внёс Артём. И внесем данные в таблицу.

Таким образом, Жене причитается 34% от 1100000 рублей.

Ответ: 374000 рублей.

Задачи на концентрацию

Среди задач на проценты популярны задачи на понятие концентрации раствора, смеси или сплава. Впервые с этим понятием можно познакомить учеников в 6 классе, решая простейшие задачи. Концентрация раствора – это процент, который составляет масса растворенного вещества от массы раствора. Учащимся 6 класса можно предложить подобрать или составить задачи из жизни, где используются понятие концентрации, например, «математика на кухне». Для учащихся более старшего возраста, изучающих химию, можно предложить следующие задачи.

1. В сосуд, содержащий 7 литров 14-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Решение. 1-й способ.

Запишем условие.

Сначала посчитаем, какой объём составляет некоторое вещество.

Затем найдем концентрацию после добавления 7 л воды: .

Ответ: 7 %.

2-й способ.

Объём увеличился в 2 раза, значит, при неизменной массе растворенного вещества, концентрация уменьшилась в 2 раза.

.

Ответ: 7%

2. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 82 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

Решение. Пусть  - это масса винограда.

Составим и решим уравнение.

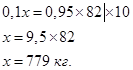
Ответ: 779 кг.

3. Смешали некоторое количество 13-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Сначала посчитаем, какой объём составляет некоторое вещество, взятого раствора.

Затем посчитаем, какой объём составляет некоторое вещество, добавленного раствора:  и концентрацию.

Ответ: 15%

4. Имеется два сплава. Первый содержит 10% никеля, второй  — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение.

Cоставим и решим систему уравнений.

Решая систему, получаем x=90, y=135. И ответим на главный вопрос задачи  кг.

Ответ: 45 кг.

5. Первый сплав содержит 5% меди, второй  — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение.

Масса меди в III сплаве равна  и равна .

Составим уравнение.

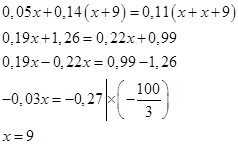
Найдем массу III сплава.

 кг.

Ответ: 27 кг.

6. Смешав 54-процентный и 61-процентный растворы кислоты и, добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?

Решение. Пусть x кг – масса 54%-го раствора кислоты, а y кг – масса 61%-го раствора, тогда

Массу растворенной кислоты можно считать равной, или . Получим уравнение 0,54x+0,61y=0,46(x+y+10).

Рассмотрев второй вариант смешивания, получим:

Массу растворенной кислоты можно считать равной 0,54x+0,61y +5, или 0,56(x+y+10). Получим уравнение 0,54x+0,61y+5 = 0,56(x+y+10).

Составим и решим систему уравнений.

Значит, масса 54%-го раствора кислоты равна 20 кг.

Ответ: 20 кг.

Сложные проценты

Если некоторая величина изменяется многократно на одинаковое число (p) процентов, то последовательность получившихся значений этой величины составляет геометрическую прогрессию, (n+1)-ый член которой вычисляется по формуле: .

1. Бизнесмен Печенов получил в 2000 году прибыль в размере 1000000 рублей. Каждый следующий год его прибыль увеличивалась на 16% по сравнению с предыдущим годом. Сколько рублей заработал Печенов за 2002 год?

Решение. Воспользуемся формулой ,где  - конечная цена, - начальная цена,  - число процентов от предыдущей цены,  - время.

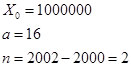
руб.

Ответ: 1345600 руб.

2. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20900 рублей, через два года был продан за 16929 рублей.

Решение. Воспользуемся формулой ,где  - конечная цена, - начальная цена, - число процентов от предыдущей цены,  - время.

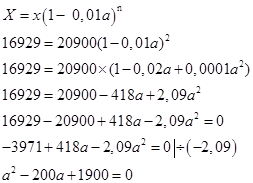
 - не удовлетворяет условию задачи

Ответ: 10 %.

3. Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 4000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2004 году, имея капитал в размере 4500 долларов, и, начиная с 2005 года, ежегодно получала прибыль, составляющую 200% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2007 года, если прибыль из оборота не изымалась?

Решение.

Воспользуемся формулой ,где  - конечная цена, - начальная цена,  - число процентов от предыдущей цены,  - время.

Сначала посчитаем капитал в 2007 г. компании "Альфа".

2007 год тоже включается во время получения прибыли.

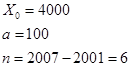
 долларов.

Затем посчитаем капитал в 2007 г. компании "Бета".

 долларов.

И ответим на вопрос, на сколько долларов капитал одной из компаний был больше капитала другой к концу 2007 года.

 долларов.

Ответ: на 1345000 долларов.

4. В четверг акции компании подорожали на некоторое число процентов, а в пятницу подешевели на то же самое число процентов. В результате они стали стоить на 36% дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?

Решение. 1-й способ.

Пусть  – начальная цена, тогда  (100-36) – конечная, а  - некоторое число процентов.

Ответ: 60%.

Заключение

В данной работе изложен опыт работы учителя-практика по использованию практико-ориентированных задач на материале «Проценты». Показано изучение данной темы на разных возрастных категориях учащихся. Решение таких задач позволяет учащимся самостоятельно выполнять задания прикладного характера, анализировать результаты, что важно в процессе реализации практико-ориентированного обучения математике. Многолетняя практика показывает, что систематическая работа по решению и конструированию практико-ориентированных задач и использование разнообразных приёмов дает положительные результаты при обучении математике.

Список источников и литературы

1. Г.В. Дорофеев, Л.Г. Петерсон «Математика», учебник для 5 класса Части 1 и 2, изд-во «ЮВЕНТА», М.- 2017

2. Г.В. Дорофеев, Л.Г. Петерсон «Математика», учебник для 6 класса Части 1,2 и 3, изд-во «ЮВЕНТА», М.- 2017

3. Алгебра. 7 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни/ [Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин]. 6-изд. – М. : Просвещение, 2017.

4. Алгебра. 9 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни/ [Ю. М. Колягин, М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин]. 6-изд. – М. : Просвещение, 2017

5. «Сборник самостоятельных и контрольных работ к учебникам математики 5 - 6 классов Г.В. Дорофеева, Л.Г. Петерсон», авт. Кубышева М.А., 2012 г. УМЦ «Школа 2000»

6. Петерсон Л.Г., Грушевская Л.А., Кубышева М.А., Рогатова М.В. Методические рекомендации к учебнику «Математика» 5 класс/ Г.В. Дорофеев, Л.Г. Петерсон «Математика», учебник для 6 класса Части 1,2 и 3, изд-во «ЮВЕНТА», М.- 2013

7. Петерсон Л.Г., Грушевская Л.А., Кубышева М.А., Рогатова М.В. Методические рекомендации к учебнику «Математика» 6 класс / Г.В. Дорофеев, Л.Г. Петерсон «Математика», учебник для 6 класса Части 1,2 и 3, изд-во «ЮВЕНТА», М.- 2013

8. www.mathege.ru

9. https://oge.sdamgia.ru/

.

Скачано с www.znanio.ru