Практикум по графам

ПРАКТИКУМ ПО ТЕОРИИ ГРАФОВ И СЕТЕЙ

Введение

1 Элементарные понятия теории графов

2. Матричное представление  графов и сетей

3. Институты и сети

4. Структуры управления и взаимодействие акторов

5. Кёнигсбергские мосты и эйлеровы циклы

ПРАКТИКУМ ПО ТЕОРИИ СЕТЕЙ

Введение

Считается, что теория графов начала формироватся в ее математических основаниях в 18 веке при решении задачи о семи мостах Кёнигсберга (Калининграда). Cреди жителей Кёнигсберга была распространена загадка: Как пройти по семи мостам города, не проходя ни по одному из них дважды? Решение считалось неизвестным. По легенде на одном из праздников ученые в шутку предложили решить ее кайзеру Вильгельму, который попросил перо и с честью вышел из положения, нарисовав дополнительный мост. Теоретическое объяснение решений обеих задач в 1736 году разработал выдающийся математик, член Петербургской академии наук Леонард Эйлер.

Теория графов нашла широкое применение в решении транспортных и коммуникационных задач, в частности, для определения маршрута данных в Интернете. Однако технические задачи не исчерпывают перспективы использования теории графов. Теория графов может применяться для количественного анализа в сфере общественных наук: экономики (торговые потоки), социологии (объемы сетевых коммуникаций), политологии (струрирование и динамика  партийных групп), медицине (пути инфекций) и т.д. История науки показывает, что первая работа по социальной теории сетей «Кто выживет? Основы социометрии, групповая психотерапия и социодрама» была написана Якобом Морено в 1934 году. Эта работа, в сущности, определила для математической теории графов целый ряд прикладных направлений в социальной сфере, которые имеют большой, пока еще недооцененный потенциал развития. В институциональной экономике применение элементов теории графов позволяет исследовать сетевое устройство экономических, политических, социальных правил-институтов (взаимодействий) на различных уровнях человеческого сообщества: между людьми, организациями или странами, которые образуют на первый взгляд сложные сети, но имеют определенную структуру и поддаются анализу.

В институциональной экономике структура транзакций, которая связывает между собой множественных участников этих отношений, создает определенные правила взаимодействия, и может рассматриваться как система специфических институтов. Изучение основ теории графов нацелено на развитие понимания сетевых взаимодействий, взаимовлияния структуры сети и эффективности взаимодействий. В дальнейшем при использовании терминов «сети» и «графы», будем понимать симметричные двухсторонние транзакции акторов, а для описания направленных односторонних воздействий используем термин «орграф» (ориентированный или направленный граф). В орграфе ребро - это упорядоченная пара вершин, его концов, что учитывается при анализе путей. Граф может быть ориентированным или нет. По ребрам неориентированного графа можно двигаться в обоих направлениях. Анализ путей из одной вершины в другую позволяет определять кратчайшие пути для любой пары точек-акторов в направленном графе, и оценивать эффективность коммуникаций.

В результате систематических занятий по теории графов и сетей студент должен

знать основные элементарные понятия  теории орграфов и сетей

уметь находить (определять, строить)

      - матричное представление (М) сетей и направленных графов по заданному графическому образу

- графический образ сети или направленного графа по заданному матричному представлению М (сети или графа)

- находить (вычислять последовательно) различные степени  K матрицы М (М^K) с использованием программы Excel. Например, программа МУМНОЖ(B15:N27;B43:N55) выдает 3-ю степень матрицы М, где B15:N27 – исходная матрица М, а (B43:N55)  - квадрат матрицы М (М²)

владеть основами социально-экономической интерпретации понятий

            - сети, графы, вершины-акторы, ребра-связи

- степень вершины

            - пути и циклы,

            - мосты, брокеры

Литература

1. Кузьминов Я.И., Бендукидзе К.А., Юдкевич М.М. Курс институциональной экономики. Гл.3: Сети в институциональном анализе.
2. Градосельская Г.В. Современные подходы к измерению сетевых взаимодействий.
3. Учебная тема: Эйлеровы графы.Материал из Saratov FIO wiki./
4. Чураков AM. Анализ социальный сетей//Социологические исследования. 2001. №1. С. 109-121.
5. Термины. Теория графов. http://dic.academic.ru/dic.nsf/ruwiki/878623

1. Элементарные понятия теории графов

АЛЬТЕРНАТИВНЫЙ ВЫБОР (поясните кратко)

1.1. Термины «акторы» и «связи»  в  теории сетей соответствуют терминам «вершины» и «ребра» в теории графов

Различие терминов исторически связано со сферой применения: сети рассматриваются в гуманитарных и технических науках, а графы – в математике.  Применение математических методов анализа сетей стирает границы применимости терминов, когда учитывается направление связей

1.2. Полный граф - граф, где для любых двух вершин существует соединяющий путь

 Правильный ответ: полный граф – это граф, у которого любые две вершины соединены одним ребром. Вместо этого дано определение Связного графа (без висячих, автономных вершин или подграфов)

1.3. Орграф – это граф, где на каждом ребре задано направление связи

Заданное направление связи означает одностороннее движение, например, денежных средств от спонсора→университету, или отчета от подчиненного→ руководителю

1.4. Размер сети –  это число вершин

Сеть – это связанный граф. Размер связанного графа равен максимальному из кратчайших путей между любыми парами вершин maxmin (l_ij). Размер сети не может быть больше, чем N-1.  N – число вершин в графе

1.5. Степень центральности актора  – это число его связей

Степень центральности актора характеризует его активность и положение (коммуникационную роль) в сети. Чем больше прямых связей, тем больше путей может проходить через него, тем выше его роль в коммуникации акторов сети

1.6. Нормированная степень центральности актора  – это число его связей, деленное на размер сети

Нормированная степень центральности актора  позволяет оценивать охват, и сравнивать активность акторов в различных сетях

1.7. При отсутствии прямой связи между акторами теория графов позволяет вычислить число путей любой длины, например 2-х (или 3-х) шаговых путей

Для этого сеть представляют как матрицу размера NxN, где в клеточке ij ставят ноль (если нет связи между акторами) и единицу (если есть). Возведение матрицы в степень 2 (или 3) с использованием программы Excel дает число 2-х (или (3-х) шаговых путей из вершины i в вершину j. Этот метод позволяет в больших сетях решать проблемы доступа к любой вершине, рассылки информации, приказов и т.д.

1.8. Цикл - это такой путь, который приводит начальной вершине

Цикл - это такой путь, который приводит начальной вершине, после обхода всех вершин.

1.9. Путь в графе или орграфе - это последовательность ребер, по которым можно поочередно проходить так, чтобы каждая вершина встречалась не более, чем однажды.

2.10.    Ребро - это неупорядоченная пара вершин, его концов  

Граф может быть ориентированным или нет. В орграфе, ребра рассматриваются как упорядоченные пары вершин: первая вершина - это начало ребра, а вторая - его конец.

МНОЖЕСТВЕННЫЙ ВЫБОР ВСЕХ ПРАВИЛЬНЫХ ОТВЕТОВ

1.8. Актором может быть

1) экономика

2) страна

3) Газпром

4) индивид

5) любой субъект социально-экономических отношений

1. 9. Реляционные связи отношений между акторами в графе могут описывать следующие типы взаимодействий:

1) реальные или потенциальные

2) новые

3) множественные: однородные и неоднородные

4) государственные

5) торговые, финансовые, информационные

2. Матричное представление  графов и сетей

Правила заполнения матрицы направленного графа:

1)      Если нумерация вершин не задана для данного графического образа сети, то для единообразия и сопоставимости матриц мы будем определять ее следующим образом. Двигая линейку вертикально слева направо, нумеруйте вершины по мере их попадания на вертикальную линию сверху вниз.

2)      Номер ячейки матрицы определяется парой чисел:

 (номер строки i; номер столбца j) = (i; j)

3)      Число, стоящее в ячейке (i; j) матрицы М^К, означает число К-шаговых связей из вершины i  в вершину  j.

4)      Если рассматривается сеть  (двустороннее направление связей между любыми вершинами), то матрицы любой степени М^К будут иметь симметричный вид относительно главной диагонали. Стрелочки связей в этом случае не рисуют.

2.1. По  данной матрице связей графа восстановите его графический образ с обозначением вершин и направлением связей. Можно ли рассматривать его как сеть?

2.2. Восстановите графический образ, является ли он сетью?

2.3. Проверьте соответствие матрицы и направленного графа

	n1	n2	n3	n4	n5	n1   n3   n5   n4   n2
n1
n2
n3
n4
n5

2.4. Заполните матрицу представления заданного орграфа

	n1	n2	n3	n4	n5	n1   n2   n4   n34   n5
n1
n2
n3
n4
n5

3. Институты и сети

3.1. Можно ли из вершины 5 не более чем за три шага попасть в вершину 4?

Ответ - НЕТ

3.2. Заполните матрицу представления заданного направленного графа. Можно ли утверждать, что акторы n4 и n5 знакомы?  

Ответ – НЕТ

	n1	n2	n3	n4	n5	n5   n1   n3   n4   n2
n1
n2
n3
n4
n5

3.3. Заполните матрицу представления заданного направленного графа. Какие общественные функции мог бы исполнять актор 4?

Вариант ответа: Закрытый архив материалов от 1, 2, 3, 5 акторов.

	n1	n2	n3	n4	n5	n1   n3   n5   n4   n2
n1
n2
n3
n4
n5

3.4. Заполните матрицу представления заданного направленного графа. Сколько 2-х шаговых путей существует  в графе? Предложите интерпретацию вершин «начальник-подчиненный».

	n1	n2	n3	n4	n5	n1   n3   n5   n4   n2
n1
n2
n3
n4
n5

Вариант ответа:  n1 – начальник; n2 – его заместитель; n5 – подчиненный; n4 – не может быть обычным подчиненным, потому что у него не должно быть 2-х начальников, но он может быть курьером на этой фирме; тогда возможно n3 – это начальник курьера или автономный сотрудник, работающий на фирме через курьера.

3.5. Заполните матрицу представления заданного направленного графа. Сколько 2-х шаговых путей существует  в графе? Предложите интерпретацию вершин как футбольных игроков на тренировке.

	n1	n2	n3	n4	n5	n1   n3   n5   n4   n2
n1
n2
n3
n4
n5

Ответ -  1) пути n1- n2- n3 или n1- n3- n4; 2) путь n5- n2- n3. Если акторы – футболисты то эти пути – футбольные передачи.  Игрок  n4, скорее всего, – вратарь, и команда  нарабатывает атаки на ворота типа n1- n2- n3- n4; n1- n3- n4; n5- n2- n3- n4, игроки n5 и  n3 могут бить прямо по воротам.

4 Структуры управления. Взаимодействия акторов

4.1. Нарисуйте направленный граф. 1) Сколько двух шаговых путей из n2 в n3?. 2) Если вершины – это группы или люди, а стрелки – предложения или указания, можно ли считать эту структуру иерархией? 3) Если да, то кто руководитель и его заместитель?

Вариант ответа:  1) Только один путь n2- n5- n4.  2) Да. 3) n5 – это руководство: совет директоров или генеральный директор; n1 – исполнительный директор и руководит головным отделом n4. Пояснение. n2 – это отдел сбыта  и планово-договорной, через них подписываются договора у директора; n3 и  n4 – это  основные производственные или аналитические отделы на этой фирме, n4 – головной. Через руководство n5 также идут также распоряжения на зарплату и отпуска.

4.2. Заполните матрицу представления заданного направленного графа. Какого типа функции может выполнять организация 4?

	n1	n2	n3	n4	n5	n1   n3   n5   n4   n2
n1
n2
n3
n4
n5

Вариант ответа:  Это может быть медицинская организация, таможня, предприятие по утилизации отходов, государственные склады, архивы, библиотеки. Это общественные, государственные или частные некоммерческие организации исполняющие заказы.

4.3. Нарисуйте направленный граф. Можно ли интерпретировать его как связи правительства с министерствами?

Вариант ответа:  Если n1 – это Правительство – центральный орган власти РФ,  а n2- n5 – это Министерства – органы исполнительной власти, то можно. Такая интерпретация возможна, потому, что Министерства, как органы исполнительной власти, самостоятельны в осуществлении своих полномочий, установленных федеральными законами, актами Президента РФ и Правительства РФ. При осуществлении этих полномочий  Министерство непосредственно взаимодействует с другими органами государственной власти и органами местного самоуправления

4.4. К какому типу связей и организаций можно отнести эту сеть на рис.1?

Расположите вершины по кругу и восстановите графический образ. Определите наличие и число трехшаговых путей

 Рис. 1 Матрица представления графа. Голубым цветом выделены связи вершин.

Ответы: Мы классифицируем это сообщество как сеть или неориентированный граф. Число трех-шаговых путей представлено на рис 2. в матрице третьей степени М³.  Цифры в ячейках этой матрицы означают число трех-шаговых путей. Наличие более коротких путей для этих ячеек(пары вершин) отображено с помощью цвета.

 Рис. 2. Матрица третьей степени М³

Голубым цветом выделены ячейки (пары вершин) сети, где помимо трехшаговых путей существуют прямые, одно-шаговые связи. Желтым цветом выделены пары вершин, где существуют двух-шаговые пути. Остальные ячейки (пары вершин) среди закрашенных выделены зеленым  цветом. Зеленые определяют пары, для которых трех-шаговый путь наиболее короткий. Незакрашенные ячейки (где стоят нули) отображают пары вершин, которые находятся более чем в трех шагах друг от друга.

4.5. К какому типу связей можно отнести сообщество на рис.3? Постройте матрицу связей. Определите размер сети.

Рекомендации по построению матрицы сети. Двигая линейку вертикально, нумеруйте вершины по мере их попадания на вертикальную линию сверху вниз. Картинка растянута, чтобы порядок был единственно очевидным для всех студентов. Здесь 2 случая попадения вершин (акторов) на одну вертикаль. Задание: Определите размер сети.

Рис. 3. Система трех офисов, с персональными коммуникациями

Решение: Порядок решения должен быть следующим 1. Построить матрицу связей и раскрасить ячейки, где есть связи. 2.  Возвести матрицу во 2-ю степень. Ячейки, где стоят не нули показывают число 2-х шаговых путей, нужно раскрасить те из них, где были прямые связи в «родной» цвет. 3. Если остались ячейки, где стоят нули в М², то вычислить следующую (третью) степень матрицы, и раскрасить известные ячейки одно-шаговых и двух-шаговых путей, и так далее. 4. После исчисления матрицы М⁵ , когда на поле матрицы не останется нераскрашенных нулей, это будет означать, что размер сети 5, потому что среди кратчайших путей в сети путь в 5 шагов максимальный, то есть, не более чем пять шагов достаточно, чтобы перейти от одной вершины к другой.

4.6. Постройте матрицу представления сети на рис 4. Двигая линейку вертикально, нумеруйте вершины по мере их попадания на вертикальную линию сверху вниз. Если в сети есть «брокеры»  и «мосты» определите номера вершин. Предложите интерпретацию вершин различного цвета. Определите размер сети.

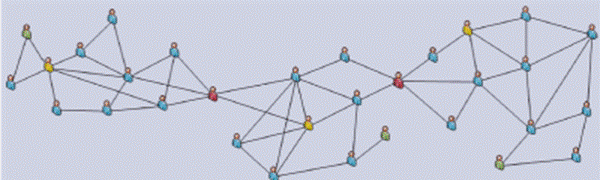
Рис. 5. Сеть с разноцветными вершинами

Решение: Брокерами являются первая из желтых вершина (№ 3) и две красные (№11 и № 20). Эти вершины обладают свойством: если их убрать, то нарушится связность графа (сети). Остальные вершины таким свойством не обладают. Мостом является случай висящей вершины или «листа», где  ребро, соединяет зелёную вершину с сетью. Желтые вершины, возможно, означают формальных руководителей  трех групп (организаций). Если вершины – это населенные пункты, то желтые вершины - формальные  региональные центры. Формальный актор или вершина-носитель может не быть одновременно лидером коммуникативности, которыми обладают другие (голубые) вершины.

4.7. Задача о мостах Кёнигсберга

Город Кенигсберг представлен в виде районов четырех автономных районов – вершин A, B, C, D, соединенных семью мостами – ребрами a, b, c, d, g, e, f.

Задача 1: можно ли  пройти по всем мостам, не проходя ни по одному из них дважды?

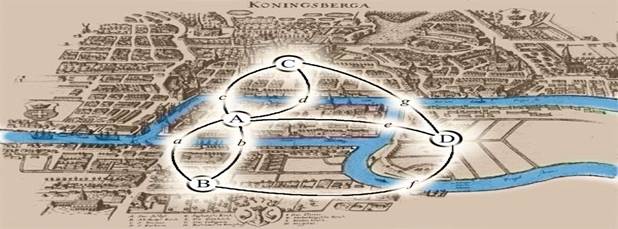
Рис. 6. Стилизованные мосты-ребра в Кёнигсберге

Задача о семи мостах была решена  Эйлером.  Эйлер доказал следующие теоремы:

1).Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.

2). Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

3. Если граф содержит более двух нечётных вершин, то обход невозможно начертить одним росчерком - решения не существует. Если граф содержит не более двух нечётных вершин, то задача имеет положительное решение.

Рис.7.  Граф Кёнигсбергских мостов

У графа кёнигсбергских мостов все четыре вершины нечётные, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Задача 2: Заполните матрицу смежности (связей), для схемы мостов-ребер города Кенигсберга.

Задача 2:  Какой мост нарисовал кайзер Вильгельм, когда его попросили решить задачу 1?

Ответы: 1) не существует, т.к. граф содержит больше двух нечетных вершин, 2) см. рис 7,

3) мост между районами С и  В.

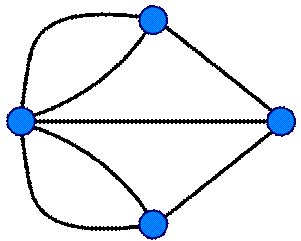
4.8. Вопрос: Существует ли Эйлеров цикл для данного на рис. 8 графа?

 Ответ: Каждая вершина графа  имеет чётную степень, поэтому этот граф — эйлеров. Обход рёбер в алфавитном порядке даёт эйлеров цикл

Рис.8.     Граф

Скачано с www.znanio.ru