Практикум СИМПЛЕКСНОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

4.5.2. Задачу из п. 2.5.3 записать в базисном виде, определить для него базисное решение и сделать выводы о его допустимости и оптимальности.

Задача 2.5.3:

Найти

При ограничениях:

Определение 4.1. Форма записи ЗЛП при наличии системы m линейно независимых ограничений задачи с n переменными, в которой m переменных выражены через остальные (n - m) переменные, называется ее базисным видом.

Здесь n = 4, m = 2.

В результате преобразования заданной системы ограничений методом Жордана-Гаусса получена система уравнений (см задачу 2.5.3, файл Tema2-zad2.doc )

А также выражение для целевой функции:

Из этой системы можно выразить х1 и х2 через х3 и х4. Получаю решение:

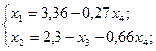
Это и есть базисный вид записи этой задачи.

Приравнивая свободные переменные х3, х4 к нулю, получаю следующее базисное решение:

Определение 4.3. Решение задачи ЛП, в котором все свободные переменные равны нулю и, следовательно, базисные переменные равны свободным членам, называется базисным.

Так как в базисном решении х1 и х2 положительны, это решение является допустимым.

Определение 4.4. Базисное решение, в котором все базисные переменные неотрицательны, является допустимым (так как по условию задачи ее переменные являются неотрицательными).

Оптимальность допустимых базисных решений можно установить на основе принципа оптимальности, который для задачи (4.4) - (4.6) заключается в том, что в выражении целевой функции, записанном через свободные переменные, все коэффициенты при таких переменных либо меньше, либо равны нулю.

Следовательно, это базисное решение не является оптимальным, так как коэффициенты при свободных переменных х3 и х4 в выражении для целевой функции ПОЛОЖИТЕЛЬНЫ.