Правила по математике для 5 класса

1.   Натуральные числа.

Для  счѐта  предметов  применяют  натуральные  числа.  Любое натуральное   число  можно   записать  с  помощью  десяти  цифр: 0,  1,  2,  3,  4,  5,  6,  7,  8,  9.  Самое  маленькое  натуральное  число  — единица  (1).  Ноль  не  относят  к  натуральным  числам.

2.   Отрезок. Луч. Прямая.

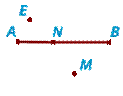Две  точки  A  и  B  соединенные  прямой линией называются   отрезком  АВ. 

Тот  же отрезок можно обозначить ВА.  Точки  А  и  В называют  концами  отрезка  AB.  Любые две  точки  можно  соединить  только  одним  отрезком.  На  рисунке   изображен   отрезок  АВ.  Точка  N  лежит  на  этом   отрезке  между 

точками  A  и  B,   а  точки  E  и  M  на  нем  не  лежат.  Точка  N  разделяет  отрезок  AB на  два  отрезка  AN  и  NB.  Их  также  можно  назвать  NA  и  BN. 

 Через любые две точки проходит одна единственная прямая.  Прямая не имеет концов.

Если прямую AB разделить точкой O, то мы получим два луча,  которые будут называться луч OB   и луч OA . Переставлять буквы  в их названиях нельзя, потому что точка O является началом этих лучей,   и названия начинаются именно с нее.    

        В отличие от прямой луч бесконечен только в одну сторону. 

3. Сложение и вычитание натуральных чисел.

Слагаемые — это числа, которые мы складываем,  а результат их сложения называется суммой.

Число, из которого вычитают, называют уменьшаемым,  а число, которое вычитают, вычитаемым.  Результат вычитания называют разностью.    

Свойства сложения и вычитания:

1)   Переместительное свойство сложения.

При перестановке слагаемых сумма не меняется.    

                                        3 + 4   =   4 + 3   =   7 .    

2)   Сочетательное свойство сложения.

Сумма трех и более слагаемых не изменится от изменения порядка сложения чисел.           a + ( b + c )   =   ( a + b ) + c .

Например:   3 + ( 7 + 2 )     =   ( 3 + 7 ) + 2     =   12 .

3)   При прибавлении нуля к числу сумма равна самому числу.  Если из числа вычесть нуль, оно не изменится.  Если из числа вычесть это число, получится нуль. 

a + 0 = a ;         a – a = 0;         a – 0 = a .

4)   Свойство вычитания суммы из числа.

В этом выражении мы вычитаем сумму из числа, можно сделать иначе, сначала вычесть из уменьшаемого одно слагаемое, а потом из полученной разности второе слагаемое. 

a – ( b + c )   =   a – b – c .

5)   Свойство вычитания числа из суммы. 

При вычитании   числа из суммы, можно вычесть его из любого слагаемого и к разности прибавить другое слагаемое.

( a + b ) – c   =   a + ( b – c ).

Периметр многоугольника — это сумма длин его сторон.

4. Уравнение.

Значение буквы, при котором уравнение — верно,  называют корнем уравнения. 

Решить уравнение —  значит найти все его корни или убедиться, что оно не имеет решения.   

1.    Чтобы найти неизвестное слагаемое, надо из суммы вычесть

известное слагаемое.                                                                                        а + 3 = 5  →  а = 5 – 3  → а = 2

2.    Чтобы найти неизвестное уменьшаемое, надо к разности

прибавить вычитаемое.                                                                                    с – 4 = 6  →  с = 6 + 4 → с = 10

3.    Чтобы найти неизвестное вычитаемое, надо из

12 – y = 5  →  y = 12 – 5 → у = 7 уменьшаемого вычесть разность. 4. Чтобы найти неизвестный множитель, надо произведение x ∙ 7 = 21  →  x = 21 : 7 → х = 3 разделить на известный множитель. 5. Чтобы найти неизвестное делимое, надо частное умножить на y : 3 = 10  →  y = 3 ∙ 10 → у = 30 делитель. 6. Чтобы найти неизвестный делитель, надо делимое разделить

20 : x = 4  → x = 20 : 4 → х = 5 на частное.

5.   Умножение натуральных чисел и его свойства.

Произведение чисел   m   и   n   —  это сумма  n   слагаемых, каждое из которых равно   m:   

5∙3 = 5 + 5 + 5.

 Выражение вида   m • n ,   а также значение этого выражения, называют   произведением чисел   m   и   n .   Числа   m   и   n   называют множителями.    

1)   Переместительное свойство.

При перестановке множителей значение произведения не меняется. m • n   =   n • m .

2)   Сочетательное свойство.

В произведении трех и более множителей при их перестановке или   изменения порядка выполнения умножения результат не меняется. 

a • (b • с)   =   (а • b) • c .

3)   Произведение любого натурального числа и единицы, равно   самому этому числу.                                                         n • 1   =   n .

4)   Произведение любого натурального числа и нуля, равно нулю.                                                             n • 0   =   0 .

Произведения с буквенными множителями записывают так: 

вместо  8 • x  пишут   8x, вместо   a • b   пишут   ab .  Также опускают знак умножения и перед скобками,   вместо   2 • (a + b)   пишут   2(а + b).

6.   Деление натуральных чисел и его свойства.

Действие, с помощью которого по произведению и одному из множителей находят второй, называют делением. 

Число, которое делят, называется делимым; число, на которое делят, называют делителем;  а результат деления частным. Частное показывает во сколько раз делимое больше делителя. 

1)            Выражение вида  а : 0  —  не имеет смысла. Делить на нуль нельзя.   

2)            В результате деления любого числа на   1   получается это же число.     а : 1   =   а.       

3)            Результатом деления двух одинаковых чисел будет единица.    

                                                             а : а   =   1 

4)            Зная, что     y  •  0   =   0     можно понять что,     0 : y   =   0 .       При делении нуля на любое число частным будет нуль.     

5)            Если нам надо найти делимое, зная делитель, неполное частное   и остаток. Надо перемножить делитель и неполное частное и   прибавить остаток.    

    Если    делитель  =  7 ,    неполное частное  =  12 ,  а остаток =1 ,   то  делимое  = 7 • 12 + 1  =  85 .  

7.   Порядок выполнения действий.

Для удобства принятия решения о последовательности выполнения   действий их разделили на две ступени:         первая ступень — сложение   и   вычитание,       вторая ступень — умножение   и   деление.    

При нахождении значения выражения действия выполняются   в следующем порядке:  

1)                 В выражении отсутствуют скобки, и оно включает в себя действия только одной ступени, то тогда все операции выполняются по порядку слева на право.  

2)                 Если в выражении отсутствуют скобки, и присутствуют действия двух ступеней. Тогда в первую очередь выполняются действия второй ступени, а во вторую действия первой ступени. Правило слева направо при выполнении действий одинаковой ступени выполняется.  

3)                 Если выражение содержит скобки, то действия в скобках выполняются в первую очередь. Остальные действия выполняются в соответствии с правилами 1. и 2.   

8.   Упрощение выражений.

Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. Это правило называется распределительным свойством умножения относительно сложения.    

                   ( a + b ) • c     =     a • c + b • c ,                   ( a – b ) • c     =     a • c   –   b • c

Например:  

              3a + 5a     =     3 • a + 5 • a       =       ( 3 + 5 ) • a     =     8a. 

Также для упрощения выражений можно применять сочетательное свойство умножения:    

                                  3х • 4 • 5     =     ( 3 • 4 • 5 ) • х     =     60х.

9.   Степень числа. Квадрат и куб числа. 

Для выражений вида   5 + 5 + 5 + 5   существует  более короткая запись 5 • 4 .  

       Аналогично сумме с одинаковыми слагаемыми, для произведения с одинаковыми множителями существует короткая запись.  

      Например:  2 • 2 • 2 • 2   =   2⁴ .  

Запись   2 ⁴   читается так, два в четвертой степени, и обозначает произведение четырех множителей, каждый из которых равен двум.    

        2 называется основанием степени и показывает, чему равны множители в произведении.    

        4 — показатель степени, показывает, сколько множителей в произведении.    

Число во второй степени   a ²   =   a • a   называют число в квадрате (в данном случае a в квадрате).    Число в третьей степени   x ³   =   x • x • x     называют число в кубе (в данном случае   x   в кубе).    

Степени чисел входящие в числовые выражения выполняются   в первую очередь.  

                2 ³ +   4 ²     =     8 + 16     =     24 ;  

                2 ² •   3 ²     =     4 • 9     =     36 .  

        Знак степени стоящий сразу за скобками предполагает произвести   вычисления в скобках, а затем полученный результат возвести в степень.  

              (2+4) ²     =   6 ²   =     36 . 

10.   Формулы. Формула скорости, пути.

Формула это математическая запись правил, в которой величины представлены в виде  общепринятых букв (переменных). 

Скорость это физическая величина, показывающая, какое расстояние пройдет объект за единицу времени. Скорость 90 км/ч обозначает, что объект за один час преодолеет 90 км.   Скорость — V     Путь — S     Время — t  Формула скорости будет выглядеть так:   V   =   S : t .

Формула нахождения пути:   S   =   V • t .

Формула нахождения времени:   t   =   S : V .

11.   Площадь.

Прямоугольник — это четырехугольник со всеми прямыми углами.   Квадрат — прямоугольник, у которого все стороны равны.  

 Площадь фигуры — это сумма площадей фигур, из которых она состоит. 

Чтобы найти площадь прямоугольника, надо длину умножить на ширину: 

                                                         S   =   a • b.  

a   —   длина;       b   —   ширина;       S   —   площадь.

Площадь квадрата:     S   =   a².

12.   Прямоугольный параллелепипед. Объем.

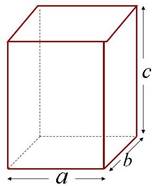
 a – длина b – ширина с – высота

 Объем прямоугольного параллелепипеда:  V = abc.

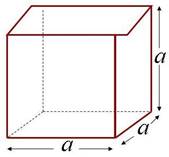
Объем куба: V = a³. 

13.   Окружность и круг.

Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R . Центр окружности обозначают буквой O. 

 Окружность разделяет плоскость на две части, внутреннюю и внешнюю. Внутренняя часть, включающая саму окружность, называется кругом.

Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет круг на два полукруга, а окружность на две полуокружности.  

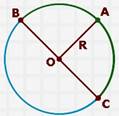Диаметр равен двум радиусам, это хорошо видно на рисунке:   D   =   2R . 

Дуга окружности — это часть окружности ограниченная двумя точками: 

 BC (дуга BC);  BAC (дуга BAC).

14.   Доли. Обыкновенные дроби.  

Длина отрезка   АВ   равна   6см.  Значит,   1см   составляет  (одну шестую)   отрезка   АВ.  

  Некоторые доли имеют особые названия:  

(одну вторую)   называют   половиной,

(одну третью)   —   третью,

(одну четвертую)   —   четвертью.

В дроби число, написанное сверху черты, называют числителем дроби, а число, написанное снизу черты   —   знаменателем дроби.  

Знаменатель обозначает, на какое количество частей разделили. А   числитель   —   сколько   таких частей взято.    

 Дроби можно изображать на координатном луче.

 Дроби, у которых числитель больше либо равен знаменателю называются неправильные, а те у которых числитель меньше знаменателя - правильными.    

При сравнении дробей надо руководствоваться следующими правилами:  

1)   Если у дробей одинаковые знаменатели, большей дробью будет та,   у которой числитель больше.  

2)   Если у дробей одинаковые числители, то большей дробью будет та,   у которой знаменатель меньше. 

При сложении дробей с одинаковым знаменателем, складываются числители, а знаменатель переписывают. 

При вычитании дробей с одинаковым знаменателем, из числителя уменьшаемого вычитают числитель вычитаемого,  а знаменатель оставляют без изменения.       

15. Десятичная запись дробных чисел.

Дроби со знаменателями 10, 100, 1000, 10 000 и т. д. принято записывать без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.

Разряды:   123, 4567

1 – сотни,  2 – десятки,  3 – единицы,  4 – десятые,  5 – сотые,  6 – тысячные,  7 – десятитысячные.

16.   Сравнение десятичных дробей.

Важно знать, что дробь 0,3 и дробь 0,30 равны друг другу. 

При сравнении десятичных дробей в первую очередь сравниваем целые части (расположены слева от запятой).   Если целые части равны тогда сравниваем дробные части.  

Если число символов после запятой у сравниваемых дробей не совпадает, тогда к дроби с меньшим количеством символов приписываем нули и сравниваем получившиеся числа дробных частей.  

Сравним 7,5 и 7,47. Припишем нуль 7,50 и 7,47:  7,50 > 7,47.

17.   Сложение и вычитание десятичных дробей.

При сложении (вычитании) десятичных дробей надо: 

1)                 при необходимости уравнять количество знаков после запятой,  добавляя нули к соответствующей дроби. 

2)                 Записать дроби так, чтобы их запятые находились друг под другом.      3) Сложить (вычесть), не обращая внимания на запятую.      4) Поставить запятую в сумме (разности) под запятыми,  складываемых (вычитаемых) дробей.    

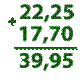
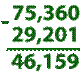
18.   Приближенные значения чисел. Округление чисел.

Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.

Если следующая за остающимся разрядом цифра равна 5, 6, 7, 8 или 9, то остающийся разряд увеличивают на 1. Если она равна 0, 1, 2, 3 или 4, то остающийся разряд оставляют без изменения.

Например:  

                        округлим до десятков       128   ≈  130;                           округлим до десятых        7,23  ≈  7,2;                           округлим до сотых           22,187  ≈  22,19;                           округлим до сотых           61,197  ≈  61,20  =  61,2.    

19.   Умножение десятичных дробей.

Умножение двух десятичных дробей выполняется так:  

1)      перемножить числа, не обращая внимания на запятую;  

2)      в полученном произведении поставить запятую так, чтобы справа от нее было столько же цифр, сколько в десятичной дроби.     

Например:  

      1,1 • 0,2   =   0,22 ;                 1,1 • 1,1   =   1,21.

При умножении десятичной дроби на   10, 100,  1000   и т. д., надо   в этой дроби перенести запятую вправо на столько знаков, сколько нулей   стоит в множителе. 

Например:  

                   0,065 • 1000   =   0065,   =   65;    

                   2,9 • 1000   =   2,900 • 1000   =   2900,   =   2900.

Вместо умножения любого числа на   0,1;   0,01;  0,001, можно разделить это число на   10 ;   100   или   1000   соответственно.         Например:  

                          22 • 0,1   =   2,2 ;        22 : 10   =   2,2 .     

20. Деление десятичных дробей.

Чтобы разделить десятичную дробь на натуральное число, надо:         1) разделить дробь на это число, не обращая внимания на запятую;       2) поставить в частном запятую, когда закончится деление целой части. 

Выполним деление  372,4 : 7.

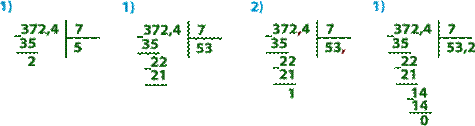
 При делении на десятичную дробь, сначала переносим запятую в делимом и делителе вправо на столько знаков, сколько их после запятой в делителе. А затем выполняем деление на натуральное число.  

    Например:    

                          543,96 : 0,3     =   5439,6 : 3   =   1813,2 ;                             237 : 0,03   =   23700 : 3   =   7900 .

При делении десятичной дроби на   10,  100,  1000,   ... ,  надо перенести запятую в этой дроби влево на столько знаков, сколько нулей в делителе.       Например:    

              34,9 : 10 = 3,49 ;       746 : 100 = 7,46 ;           28,1 : 1000 = 0,0281 .