Предмет стереометрии. Аксиомы стереометрии.

Урок 1. Тема: Предмет стереометрии. Аксиомы стереометрии.

Цели урока:                                                                                                                               Образовательные (учебные): ознакомить учащихся с содержанием курса стереометрии; изучить аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве; учить применять аксиомы стереометрии при решении задач.                                                   Воспитательные: показать, что новые понятия не изолированы друг от друга, а представляют определенную систему знаний, все звенья которой находятся во взаимной связи, сформировать навыки работы с книгой, эстетические навыки при оформлении записей, выполнении чертежей, стремление к самореализации.                                      Развивающие:  развить  творческую  деятельность (интуицию,  пространственное воображение,  смекалку);  мыслительную  деятельность (умения  анализировать, обобщать,  классифицировать).                                                                                                                             Тип урока: урок изучения нового материала.                                                                                      Технология обучения: технология критического мышления с использованием элементов проблемного обучения.                                                                                                                               Методы обучения: репродуктивный, наглядно-иллюстративный.

Ход урока.

1. Организационный момент.
2.Сообщение темы и целей урока.                                                                                                                                   3. Изучение нового материала.
Учитель: Уже три года, начиная с 7 класса, мы с вами изучаем школьный курс геометрии. Вопросы учащимся:
- Что такое геометрия? (Геометрия – наука о свойствах геометрических фигур)
- Что такое планиметрия? ( Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости)
- Какие основные понятия планиметрии вы знаете? (точка, прямая)
Учитель: Сегодня мы приступаем к изучению нового раздела геометрии – стереометрии. Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве. Стереометрия – греч.слово («стереос» - объемный, пространственный и «метрео» - измерять).    (Учащиеся делают запись в тетрадь).                                                                                    Основные понятия пространства: точка, прямая, плоскость.
Представление о плоскости дает гладкая поверхность стола, стены, пола, потолка и т.д. Плоскость, как геометрическую фигуру, нужно представлять простирающейся во все стороны, бесконечной. Обозначаются плоскости греческими буквами α, β, γ и т. д.
1. Назовите точки, лежащие в плоскости β; не лежащие в плоскости β.
2. Назовите прямые: лежащие в плоскости β; не лежащие в плоскости β.                                            Об основных понятиях (точка, прямая, плоскость) мы имеем наглядное представление и определения им не даются. Их свойства выражены в аксиомах.
Наряду с точкой, прямой, плоскостью в стереометрии рассматривают геометрические тела (куб, параллелепипед, цилиндр, тетраэдр, конус и др.), изучают их свойства, вычисляют их площади и объемы. Представление о геометрических телах дают окружающие нас предметы.                                                                                                                                        Вопросы учащимся:
- Какие геометрические тела вам напоминают предметы, изображенные на этих рисунках.
- Назовите предметы из окружающей вас обстановки (нашей классной комнаты) напоминающие вам геометрические тела.

Практическая работа ( в тетрадях).
1. Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром).
2. Обозначьте вершины куба заглавными буквами АВСДА₁В₁С₁Д_1.
3. Выделите цветным карандашом:
вершины А, С, В₁, Д₁; отрезки АВ, СД, В₁С, Д₁С; диагонали квадрата АА₁В₁В.
Обратить внимание учащихся на видимые и невидимые линии на рисунке; изображение квадрата АА₁В₁В в пространстве.                                                                                                         Вопросы к учащимся:
- Что такое аксиома?  (Аксиома – это утверждение о свойствах геометрических фигур, принимается в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия).                                                                                                            - Какие аксиомы планиметрии вы знаете?                                                                                               1) Через любые две точки можно провести прямую, и притом только одну.                                                                  2) Из трех точек прямой одна, и только одна лежит между двумя другими.
В пространстве основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

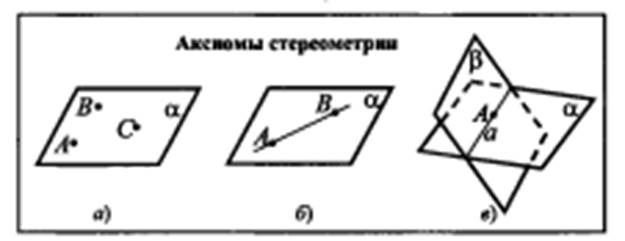
Учащиеся делают записи и рисунки в тетрадях.
Аксиома 1.  Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

Отметить, что если взять не 3, а 4 произвольные точки, то через них может не проходить ни одна плоскость, то есть 4 точки могут не лежать в одной плоскости.

Аксиома 2.   Если 2 точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

 Точки уж всегда отыщут способ,

плоскости любой, чтоб рассказать

Что какой та ни была б хорошей,

                                                могут в ней лежать,  иль не лежать.

Вопрос учащимся:
- Сколько общих точек имеют прямая и плоскость? (рис.1 – бесконечно много; рис.2 – одну)

Аксиома 3.  Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В этом случае говорят, что плоскости пересекаются по прямой.

3. Закрепление изученного материала. Решение задач из учебника.

№1 стр.7

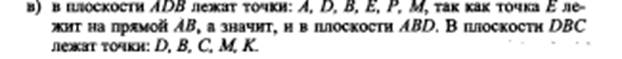
№ 2 ( а, б, д) стр.7

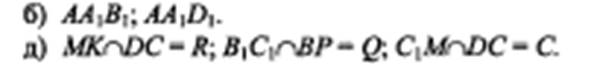
4. Подведение итогов урока. Вопросы учащимся:

1. Как называется раздел геометрии, который мы будем изучать в 10-11 классах?
2. Что такое стереометрия?
3. Сформулируйте с помощью рисунка аксиомы стереометрии, которые вы изучили сегодня на уроке.
4. Домашнее задание. п.1, п. 2, № 2 (в,г), №3, №4.