
Преобразование целого выражения в многочлен
Цели: продолжить формирование умения преобразовывать целые выражения; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
1. Какие из следующих выражений являются целыми:
а) 3x2 – 2a; в) ![]() ; д)
; д) 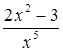 – 4;
– 4;
б) ![]() ; г)
; г) ![]() ; е)
; е)
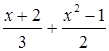 ?
?
2. Преобразуйте в многочлен.
а) ![]() в) (x – 5) (y
– 2);
в) (x – 5) (y
– 2);
б) (–x
– 4)2; г) 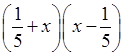 .
.
II. Формирование умений и навыков.
1. № 923.
Решение:
Преобразуем данное выражение:
![]()
![]()
При любом целом п первое слагаемое полученной суммы делится на 6, а второе слагаемое не делится на 6. Значит, ни при каком целом п сумма 6п + 10 не делится на 6.
2. № 925.
Решение:
а) x (x + 2) (x – 2) – x (x2 – 8) = 16.
x (x2 – 4) – x3 + 8x = 16;
x3 – 4x – x3 + 8x = 16;
4х = 16;
х = 4.
Ответ: 4.
б) 2y (4y – 1) – 2 (3 – 2y)2 = 48.
8y2 – 2y – 2 (9 – 12y + 4y)2 = 48;
8y2 – 2y – 18 + 24y – 8y2 = 48;
22у = 66;
у = 3.
Ответ: 3.
3. № 927 (а).
Решение:
а) Упростим данное выражение:
![]()
– a4 + 2a2 – 1 – 2a2 + 6
= a4 – 1 – a4 + 5 = 4.
Значит, значение выражения не зависит от а.
4*. № 999 (а).
Решение:
а) ![]()
![]()
![]() a4 – 4a2 +
11 –
a4 – 4a2 +
11 –
– a4 – a3 + 2,5a2 – 1,5a
+ 6 = –a3 – 1,5a2 – 1,5a + 17.
III. Проверочная работа.
Вариант 1
1. Преобразуйте в многочлен.
а) (c + 2) (c – 3) – (c + 1) (c + 3);
б) ![]()
в) ![]()
2. Найдите значение выражения
(3a
+ b)2 – (3a – b)2 при a
= 3![]() , b = –0,3.
, b = –0,3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Вариант 2
1. Преобразуйте в многочлен.
а) (a – 5) (a + 1) – (a – 6) (a – 1);
б) (a – 4) (a + 4) – 2a (3 – a);
в) (p + 3) (p – 11) + (p + 6)2.
2. Найдите значение выражения
(4x
– y)2 – (4x + y)2 при x
= 1![]() , y = –0,2.
, y = –0,2.
3. Упростите выражение (2x – 5)2 – 2 (7x – 1)2.
IV. Итоги урока.
Домашнее задание: № 924; № 926; № 928 (а); № 929 (а).
Вариант 1
1. Преобразуйте в многочлен. а) (c
+ 2) (c – 3) – (c + 1) (c + 3); б) ![]() в)
в) ![]()
2. Найдите значение выражения (3a
+ b)2 – (3a – b)2 при a
= 3![]() ,
b = –0,3.
,
b = –0,3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Вариант 2
1. Преобразуйте в многочлен.а) (a – 5) (a + 1) – (a – 6) (a – 1); б) (a – 4) (a + 4) – 2a (3 – a); в) (p + 3) (p – 11) + (p + 6)2.
2. Найдите значение выражения (4x
– y)2 – (4x + y)2 при x
= 1![]() ,
y = –0,2.
,
y = –0,2.
3. Упростите выражение (2x – 5)2 – 2 (7x – 1)2.
Вариант 1
1. Преобразуйте в многочлен. а) (c
+ 2) (c – 3) – (c + 1) (c + 3); б) ![]() в)
в) ![]()
2. Найдите значение выражения (3a
+ b)2 – (3a – b)2 при a
= 3![]() ,
b = –0,3.
,
b = –0,3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Вариант 2
1. Преобразуйте в многочлен.а) (a – 5) (a + 1) – (a – 6) (a – 1); б) (a – 4) (a + 4) – 2a (3 – a); в) (p + 3) (p – 11) + (p + 6)2.
2. Найдите значение выражения (4x
– y)2 – (4x + y)2 при x
= 1![]() ,
y = –0,2.
,
y = –0,2.
3. Упростите выражение (2x – 5)2 – 2 (7x – 1)2.
Вариант 1
1. Преобразуйте в многочлен. а) (c
+ 2) (c – 3) – (c + 1) (c + 3); б) ![]() в)
в) ![]()
2. Найдите значение выражения (3a
+ b)2 – (3a – b)2 при a
= 3![]() ,
b = –0,3.
,
b = –0,3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Вариант 2
1. Преобразуйте в многочлен.а) (a – 5) (a + 1) – (a – 6) (a – 1); б) (a – 4) (a + 4) – 2a (3 – a); в) (p + 3) (p – 11) + (p + 6)2.
2. Найдите значение выражения (4x
– y)2 – (4x + y)2 при x
= 1![]() ,
y = –0,2.
,
y = –0,2.
3. Упростите выражение (2x – 5)2 – 2 (7x – 1)2.
Вариант 1
1. Преобразуйте в многочлен. а) (c
+ 2) (c – 3) – (c + 1) (c + 3); б) ![]() в)
в) ![]()
2. Найдите значение выражения (3a
+ b)2 – (3a – b)2 при a
= 3![]() ,
b = –0,3.
,
b = –0,3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Вариант 2
1. Преобразуйте в многочлен.а) (a – 5) (a + 1) – (a – 6) (a – 1); б) (a – 4) (a + 4) – 2a (3 – a); в) (p + 3) (p – 11) + (p + 6)2.
2. Найдите значение выражения (4x
– y)2 – (4x + y)2 при x
= 1![]() ,
y = –0,2.
,
y = –0,2.
3. Упростите выражение (2x – 5)2 – 2 (7x – 1)2.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.