Презентация- урок по геометрии 10 класс на тему "Нахождение объемов тел"

Автор: учитель математики Варенко О.В., Иркутская область, г. Ангарск, МБОУ «СОШ №14»

 

Тема: Нахождение объемов  тел

№ урока: 1-ый урок в теме

Предмет: геометрия

Класс: 11 классы

Цели и задачи урока:

1)                   ввести понятие объема тел его свойств, единиц измерения объёма, познакомить с объёмами параллелепипеда, куба, прямой призмы, пирамиды, цилиндра и конуса, руководствуясь наглядно-иллюстративными соображениями;

2)                   учить сравнивать,  сопоставлять, анализировать, делать выводы, развивать правильную математическую речь, целесообразную вариативности математических упражнений, закрепить знания в результате решения задач на  применение новых формул объема;

3)                  воспитывать трудолюбие, внимательность; развитие интереса учащихся к предмету математика, активизация мыслительной деятельности, развитие математической речи, расширение математического кругозора у учащихся, научить учащихся мыслить логически, быстро думать и принимать правильные решения;

ПЕДАГОГИЧЕСКИЕ ВОЗМОЖНОСТИ:

·                     повышение уровня математического мышления,

·                     углубление теоретических знаний,

·                     расширение кругозора,

·                     возникновение интереса к математике,

·                     воспитание стремления к совершенствованию своих знаний,

·                     формирование умений коллективного поиска ответов на вопросы,

·                     сплочение коллектива, формирование дружеских, товарищеских отношений

Использовалась дополнительная литература:

                  Все рисунки и чертежи выполнены автором данной работы- Варенко Оксаной Валентиновной в программах:  Microsoft Office Word, Paint.

                  В данной работе использованы фотографии c сайтов:

-           ru.wikipedia.org›wiki/Конус_выноса

-                      images.yandex.ru›конус нарастания

-                      medusy.ru›diving/yad_mollusk/index.shtm

-                      reinesland.ru›wiki/Телесный_угол

 

Планируемые результаты:

- Личностные: Проявляют положительное отношение к урокам математики, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; адекватно воспринимают оценку учителя и одноклассников

Предметные: выводят формулы , для нахождения объемов тел; исследуют ситуации, требующие применения данных формул, используют выведенные формулы, для решения задач.

Метапредметные: передают содержание в сжатом , выборочном или развёрнутом виде; определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств её достижения; умеют оформлять мысли в устной и письменной речи с учётом ситуации.

 

Межпредметные связи: алгебра, черчение.

 

Формы деятельности: фронтальная; индивидуальная

Формы обучения: смешанная

Ресурсы:

Основные: ПК учителя; учебник; презентация по теме

Дополнительные: видеоурок по теме

 

 

 

                                                              Ход урока:

1,Организационный этап

Учитель: Сегодня на уроке мы с вами введем понятие объема тел его свойств, познакомимся и узнаем  единицы измерения объёма, познакомимся с объёмами параллелепипеда, куба, прямой призмы, пирамиды, цилиндра и конуса, руководствуясь наглядно-иллюстративными соображениями.

 

Подобно тому как все искусства тяготеют к музыке,

                        все науки стремятся к математике.

                                                                   Д. Сантаяна

   Геометрия есть искусство правильно рассуждать

                              на неправильных чертежах.

                                                                  Пойа Д.

2. Постановка цели и задачи урока. Мотивация учебной деятельности учащихся

 

   Повторение с частичным (первичным)  введением нового материала.    ( повторить известные многогранники и тела вращения- определения и чертежи – заранее заготовленных карточках)

                                              Найдите соответствия

Название	Чертеж
Конус
Прямоугольный параллелепипед
Пирамида
Сфера
Куб
Призма
Цилиндр

 

3.  Изучение нового материала в сравнении – «Планиметрия- Стереометрия».

 Понятие объема тела вводится  по аналогии с понятием площади плоской фигуры. Из курса планиметрии известно, что каждый многоугольник имеет площадь, которая измеряется с помощью выбранной единицы измерения площадей. В качестве единицы измерения площадей обычно берут квадрат, сторона которого равна единице измерения отрезков.

Площадь многоугольника- это положительная величина  той части плоскости , которую занимает многоугольник.

Аналогично будем считать, что каждое из рассматриваемых нами тел имеет объем, который можно измерять с помощью выбранной единицы измерения объемов.

Объем тела – это положительная величина той части пространства , которую занимает геометрическое тело.

 

В чем измеряется площадь плоских фигур?

                  Какие единицы измерения площадей вы уже знаете?

За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков.

   1 км², 1 м², 1 дм², 1 см²,  1 мм² , 1 а, 1 га и т.д.

За единицу измерения объемов примем куб,  ребро которого равно единице измерения отрезков.

      Куб  с ребром 1 см называют кубическим сантиметром и обозначают см^3.

      Аналогично определяют 

1 м³, 1 дм³, 1 см³ , 1 мм³ и т.д.

Процедура измерения объемов тел аналогична процедуре измерения площадей. При выбранной единице измерения объем каждого тела  выражается положительным числом, которое показывает . сколько единиц  измерения объемов  и частей единицы содержится в данном теле.

 

Мы с вами уже знакомы из курса планиметрии со свойствами площадей.

Давайте вспомним   первое свойство:   ( ученики используют подсказку на слайде)-

Равные многоугольники имеют равные площади

    Мы с вами можем сформулировать первое свойство объема тел используя в качестве подсказки рисунок слайда- Равные тела имеют равные объемы

Равенство двух фигур, в частности двух тел, в стереометрии определяется так же, как и в планиметрии: два тела называются равными, если их можно совместить наложением

 

Рассмотрим еще одно свойство объемов.

Для этого мы вспомним второе свойство из курса планиметрии: ( ученики используют подсказку на слайде).    Свойство 2:- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

   S_F=S_F1+S_F2+S_F3+S_F4

Итак давайте выведем второе свойство объема : Если тело составлено из нескольких тел , то его объем равен сумме объемов этих тел.

        V_F=V_F1+V_F2

 

 

Мы с вами вспомнило некоторые свойства из курса планиметрии и рассмотрели 2 свойства объемов.

Сформулируйте – какие фигуры называются равновеликими? Равновеликими называются геометрические фигуры, имеющие равные площади  S_F=S_{F1 .}

Сформулируйте – какие тела называются равновеликими? Равновеликими называются тела, объемы которых равны V_F=V_F1

 

 

В стереометрии  мы с вами  будем  рассматривать объемы многогранников и объемы тел вращения

-Назовите известные вам многогранники и фигуры вращения ?  ( учащиеся должны назвать- прямоугольный параллелепипед, куб, призма, пирамида, цилиндр, конус, сфера и шар)

 

3-б .   Введение формул объемов тел через диалог учителей и учащихся.

        В курсе математики 5 –го класса мы с вами уже познакомились с прямоугольным параллелепипедом. Давайте воспользуемся чертежом и вспомним  основные элементы прямоугольного параллелепипеда и формулы уже известные нам.

                Измерения -    а-длина  ; b-ширина; с- высота

Известные формулы:

V=a^.b^.c

S_осн= a^.b

V=S_осн^.H

Следствие1: Объем прямоугольного параллелепипеда равен произведению площади основания на высоту

 

А как называется прямоугольный параллелепипед у которого все измерения равны?    Куб

Длина куба   а =а;   ширина  в=а  ; высота   с=а

Подставим имеющиеся данные в формулу V=a^.b^.c  в результате чего мы получаем

( ученики сами выводят формулу нахождения объема куба)

 V=a^.а^.а= а³

V=а³

 

А сейчас мы  рассмотрим прямую призму, основанием которой является прямоугольный треугольник  (используем рисунок на слайде)

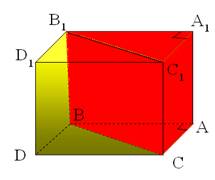Ученики вспоминают, что прямая призма, основанием которой является прямоугольный треугольник образуется путем разрезания прямоугольного параллелепипеда на две равные части. Они могут самостоятельно определить формулу для нахождения объема прямой призмы

 

V_парал=S_осн^.H

S _осн=2^.S_ABC

_{По свойству объемов}

V_парал= 2^.S_ABС^.H

 

V _призмы = (V _парал) :2

V _призмы = (2^.S_ABС^. H): 2

V _призмы = S_ABС^. H

Следствие 2- Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению основания на высоту.

 

А сейчас мы с вами найдем объем пирамиды. Достроим пирамиду

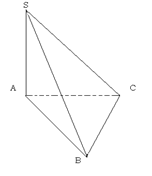ABCS до призмы.  Достроенная  призма будет состоять из 3  пирамид- SABC, SCC₁B_1, SCBB_1.      У 2 и 3 пирамиды-    SC- общая, треугольник CC₁B₁= треугольнику CBB₁

У 1 и 3 пирамиды-    СS- общая, треугольник SAB= треугольнику BB₁S

 V₁=V₂=V₃

V призмы= 3 V пирам

                          

 

 

Vпирамиды=1  V призмы

                        3

Vпирамиды=1 Sосн ^.H

                        3

Мы с вами узнали и вывели несколько формул для нахождения объемов тел. А сейчас поработаем с телами вращения.

-Какие  тела вращения вы уже знаете?  Цилиндр. Конус, усеченный конус, сфера и шар

Давайте выведем с вами формулу для нахождения объема цилиндра.

Вспомним обозначения и уже известные нам формулы, которые мы применяли для нахождения элементов цилиндра.

Обозначения:

 R -  радиус основания

 H -  высота

 L  -  образующая

 L=H

 V -  объем цилиндра

  Sосн= ПR²

Говорят, что призма вписана в цилиндр, если ее основания вписаны в основания цилиндра и призма описана около цилиндра, если ее основания описаны около оснований цилиндра. Ясно, что высота любой призмы, вписанной в цилиндр или описанной около него равна высоте самого цилиндра.

Теорема:  Объем цилиндра равен произведению площади основания на высоту.

V = ПR²H         V= Sосн ^.H  

 

 Назовите мне фигуру вращения, которую вы видите на данном слайде?  Конус

Давайте вспомним основные обозначения конуса и все уже известные нам формулы, которые мы применяем при решении задач на нахождение элементов конуса.

ОБОЗНАЧЕНИЯ:

     R - радиус основания

     L - образующая конуса
     H – высота

    V – объем

    Пирамида вписана в конус, если ее основания вписаны в основания конуса и пирамида описана около конуса, если ее основания описаны около оснований конуса. Ясно, что высота любой пирамиды, вписанной в конус или описанной около него равна высоте самого конуса. Так как мы уже знаем с вами , что объем пирамиды равен : Vпирамиды=1 Sосн ^.H

                                                                                                                              3

 

Тогда и  V_конуса =  1 Sосн ^.H   , а  в основании конуса лежит круг, то Sосн =ПR²Н

                               3  

Поэтому    V= 1 ПR²Н

                          3                           

 

 

4. Это интересно: ( межпредметные связи)

 

 

В биологии есть понятие "конус нарастания". Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
	В геологии существует понятие "конус выноса". Это форма рельефа, образованная скоплением обломочных пород, вынесенных горными реками на предгорную равнину или в более плоскую широкую долину
В физике встречается понятие "телесный угол". Это конусообразный угол, вырезанный в шаре.
	"Конусами" называется семейство морских молюсков подкласса пережнежаберных. Укус конусов очень опасен. Известны смертельные случаи.

 

5. Закрепление материала

 

                                                    Проверь свои знания:

                  Сформулируйте понятие объема.

                  Сформулируйте основные свойства объемов  тел.

                  Назовите единицы измерения объема тел.

                  Назовите формулу для измерения  объема:

- прямоугольного параллелепипеда; 

- объема куба;

- объем прямой призмы;

- объем пирамиды;

- объем цилиндра

-  объем конуса.

                  Изменится ли объем цилиндра, если радиус его основания увеличить в 2 раза, а высоту уменьшить в 4 раза?

Решение:

V =  ПR²H      V= П(2R)^{2 .}H   = П4R^2. H   = ПR^2. H

                                            4                4

                  Основаниями двух пирамид с равными высотами являются четырехугольники с соответственно равными сторонами. Равны ли объемы этих пирамид?

                  Из каких тел состоит тело, полученное вращением равнобедренной трапеции вокруг большего основания?

 

6.   Домашняя работа: Выучить формулы объемов тел, определения.

                          № 648(а,в), № 685, № 666(а,в)

 

7 :   Закрепление изученного материала:

(Разноуровневые задания, коррекция знаний).

 

Итак,  мы с вами изучили объемы некоторых многогранников и тел вращения. Давайте с вами закрепим пройденный материал.

  Для его закрепления предлагаю вам решить несколько задач.

                          Задача 1

     Три латунных куба с ребрами 3см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба?

 

Для самостоятельного решения учащимся дается несколько минут. Ученики могут решать данную задачу самостоятельно, могут воспользоваться помощью более сильных учеников. Решение проверяется по действиям.

Решение:

V_F=V_F1+V_F2 +V_F3

V_F1=3³ =27 (см³)

V_F2=4³ =64 (см³)

V_F3=5³ =125 (см³)

V_F=27+64 +125=216 (см³)

V_F=а³

а³=216 (см³)

а=  6 (см)

Ответ: ребро куба равно 6 см.

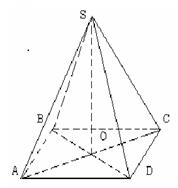
Задача 2

Найдите объем правильной четырехугольной пирамиды, высота которой равна 12 см, а сторона основания 13 см.

 

 

Решение данной задачи рассматривается классом в совместной работе.   

Решение:

V= 1  Sосн ^. H

      ³

ABCD- квадрат

S _ABCD=a²    

S _ABCD= 13²=169

V= 1  169 ^. 12 =676 (см³)

       ³

Ответ: Объем правильной четырехугольной пирамиды равен 676 см³

 

Задача 3

Решение данной задачи носит индивидуальный характер.

 

Найдите объем цилиндра, если радиус его основания равен 6см, а высота 8 см.

 

Решение

         V = ПR²H

         V =П ^. 6^{2 .} 8 =288П (см³)

        Ответ: объем цилиндра  равен 288 П см³ .

 

 

8.Заключение урока:   Итак, мы заканчиваем с вами знакомство с понятием объем, с некоторыми формулами для нахождения объема многогранников и тел вращения. С остальными формулами мы продолжим знакомство на следующих уроках стереометрии.

 

9. Рефлексия. Перед вами находятся листочки с рисунками, на которых я предлагаю вам поставить знак  вашего отношения к проведенному уроку и написать понравился ли вам урок и что в нем вам понравилось.

 

 

Скачано с www.znanio.ru