
Приближённые вычисления, погрешности. Вычисление значений простейших функций
Приближенные вычисления – вычисления, производимые над числами, которые известны нам с определенной точностью, например, полученными в эксперименте. Выполняя вычисления, всегда необходимо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большей точностью, если в данной задаче не допускают или не требуют это и наоборот.
Абсолютная разница между точным числом х и его приближенным числом а называется погрешностью данного приближенного числа.
![]()
Относительная погрешность: ![]()
Дано П=3,14. Найти абсолютную и относительную погрешности.
Результаты: 0,159 и 3,14159.
Абсолютная: ![]() П=3,14159-3,14=0,00159
П=3,14159-3,14=0,00159
Относительная: ![]()
Значащие цифры – все цифры числа, начиная с первого, отличной от нуля, до последней, за правильность которой можно ручаться.
Приближенные числа
следует записывать, сохраняя только верные знаки. Например, если абсолютная
погрешность числа 52438=100, то это число должно быть записано ![]()
52400=524*102=0,524*105.
Значащие цифры: все кроме 0.
Если число а=47,542, полученное в результате действия над приближенными числами и Е=0,1%, то а имеет три верных знака, равных 47,5.
Если приближенное число содержит лишние знаки, то его следует округлить. При округлении сохраняются только верные знаки, лишние знаки отбрасываются, причем, если первая отбрасываемая цифра больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.
Результат действий над приближенными числами представляет собой также приближенное число. Число значащих цифр результата можно вычислить при помощи следующих правил:
1) при сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.
47,541+65,4385=112,9795
Ответ: 112,90
65,4385-47,541=17,8975
Ответ: 17,898
2) при умножении и делении приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.
Приближенные вычисления с помощью
дифференциалов: ![]()
![]()
![]()
В качестве х0 выбираем (подбираем) «хорошее» значение, чтобы корень был целым, х0=64
Тогда 67=64+3, ![]()
![]() =4
=4
f(x0)=f(64)= ![]() =4
=4
![]()
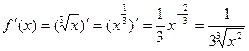
![]()
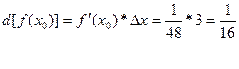
![]()
Ответ: ![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.